Đề bài
Tính diện tích phần gạch sọc trên hình sau (theo kích thước đã cho trên hình)
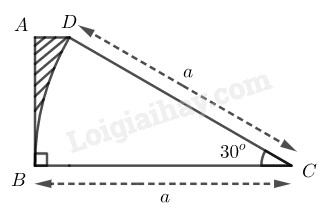
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng cạnh huyền nhân với \(\sin\) góc đối hoặc \(\cos\) góc kề.
+) Diện tích hình thang bằng nửa tổng hai đáy nhân với chiều cao.
+) Diện tích hình quạt tròn bán kính \(R,\) cung \(n^\circ\) được tính theo công thức: \(S=\dfrac{\pi R^2n}{360}.\)
Lời giải chi tiết
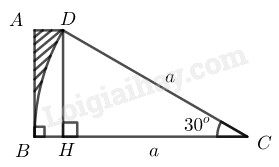
Diện tích phần gạch sọc là hiệu giữa diện tích hình thang \(ABCD\) và diện tích hình quạt tròn có góc ở tâm \(30^0\) của đường tròn bán kính bằng a.
Từ \(D\) kẻ \(DH \bot BC\), suy ra \(ADHB\) là hình chữ nhật.
Trong tam giác vuông \(HDC\) có \(\widehat {DHC} = {90^0}\)
\(DH = DC.\sin \widehat{C} = a.\sin {30^0} = \displaystyle{a \over 2}\)
\(CH = DC.\cos\widehat C = a.\cos{30^0} =\displaystyle {{a\sqrt 3 } \over 2}\)
\(BH = BC - HC = \displaystyle a - {{a\sqrt 3 } \over 2} \)\(= \displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2}\)
\( \Rightarrow AD =BH= \displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2}\) (do \(ADHB\) là hình chữ nhật)
Diện tích của hình thang \(ABCD\) bằng:
\(\displaystyle{{AD + BC} \over 2}.DH \)\(=\displaystyle{{\displaystyle{{a\left( {2 - \sqrt 3 } \right)} \over 2} + a} \over 2}.{a \over 2}\)
\( = \displaystyle {{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8}\)
Diện tích hình quạt tròn bằng: \(\displaystyle{{\pi .{a^2}.30} \over {360}} = {{\pi {a^2}} \over {12}}\)
Diện tích phần gạch sọc:
\(S = \displaystyle{{{a^2}\left( {4 - \sqrt 3 } \right)} \over 8} - {{\pi a} \over {12}}\)
\( = \displaystyle{{3{a^2}\left( {4 - \sqrt 3 } \right) - 2\pi {a^2}} \over {24}}\)
\( = \displaystyle{{{a^2}} \over {24}}\left( {12 - 3\sqrt 3 - 2\pi } \right)\)
soanvan.me
