Đề bài
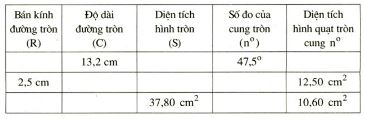
Điền vào ô trống trong bảng sau (làm tròn kết quả đến chữ số thập phân thứ nhất)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Độ dài đường tròn bán kính \(R\) là: \(C=2\pi R.\)
+) Độ dài cung tròn \(n^0\) của đường tròn bán kính \(R\) là: \(l = \dfrac{{\pi Rn}}{{180}}.\)
+) Diện tích hình tròn bán kính \(R\) là: \(S=\pi R^2.\)
+) Diện tích cung tròn \(n^0\) của đường tròn bán kính \(R\) là: \(S = \dfrac{{\pi R^2n}}{{360}}.\)
Lời giải chi tiết
- Dòng thứ nhất:
\( R\) = \(\dfrac{C}{2\pi }\) = \(\dfrac{13,2}{2. 3,14 }\) \(≈ 2,1\) (\(cm\))
\(S = π. R^2 = 3,14.{(2,1)}^2 ≈ 13,8 \)(\(cm^2\))
\({S_{quạt}}\)\(=\dfrac{\pi R^{2}n^{\circ}}{360^{\circ}}\) \(=\dfrac{3,14 .2,1^{2}.47,5}{360}\) \(≈ 1,83\) (\(cm^2\))
- Dòng thứ hai:
\(C = 2πR = 2. 3,14. 2,5 = 15,7\) (cm)
\(S = π. R^2 = 3,14.{(2,5)}^2 ≈ 19,6\) (\(cm^2\))
\(n^0\)\(=\dfrac{S_{quat}.360^{\circ}}{\pi R^{2}}\)\(=\dfrac{12,5.360^{\circ}}{3,14.2,5^{2}}\)\(≈ 229,3^0\)
- Dòng thứ ba:
\(R\) \(=\sqrt{\dfrac{s}{\pi }}\) \(=\sqrt{\dfrac{37,8}{3,14 }}\) \(≈ 3,5\) (\(cm\))
\(C = 2πR = 22\) (\(cm\))
\(n^0\)\(=\dfrac{S_{quạt}.360^{\circ}}{\pi R^{2}}\) \(=\dfrac{10,6.360^{\circ}}{3,14.3,5^{2}}\) \(≈ 99,2^0\)
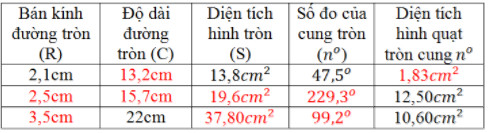
Điền vào các ô trống ta được các bảng sau: