Đề bài
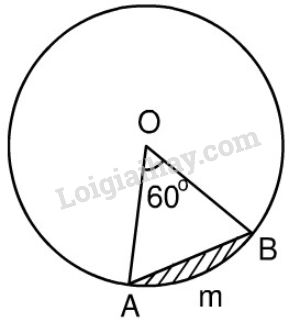
Hình viên phân là hình tròn giới hạn bởi một cung tròn và dây căng cung ấy. Hãy tính diện tích hình viên phân \(AmB\), biết góc ở tâm \(\widehat {AOB} = {60^0}\) và bán kính đường tròn là \(5,1 cm\) (h.64)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Diện tích hình viên phân = Diện tích cung tròn \(AmB\) - Diện tích tam giác \(OAB.\)
+) Diện tích quạt tròn bán kính \(R\) và có số đo cung \(n^0\) là \(S=\dfrac {\pi R^2 n}{360}\)
Lời giải chi tiết
\(∆OAB\) là tam giác đều có cạnh bằng \(R = 5,1cm\).
Áp dụng công thức tính diện tích tam giác đều cạnh \(a\) là \(\displaystyle {{{a^2}\sqrt 3 } \over 4}\) ta có
\(\displaystyle {S_{\Delta OBA}} ={{{R^2}\sqrt 3 } \over 4}\) (1)
Diện tích hình quạt tròn \(AOB\) là:
\(\displaystyle {{\pi .{R^2}{{.60}^0}} \over {{{360}^0}}} = {{\pi {R^2}} \over 6}\) (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
\(\displaystyle {{\pi {R^2}} \over 6} - {{{R^2}\sqrt 3 } \over 4} = {R^2}\left( {{\pi \over 6} - {{\sqrt 3 } \over 4}} \right)\)
Thay \(R = 5,1\) ta có \(S\)viên phân ≈\( 2,4\) \((cm^2)\)
soanvan.me
