Đề bài
Hình viên phân là phần hình tròn bao gồm giữa một cung và dây trước cung ấy. Hãy tính diện tích hình viên phân AmB theo R. Biết góc ở tâm \(\widehat {AOB} = 120^\circ \) và bán kính hình tròn là R.
Phương pháp giải - Xem chi tiết
Sử dụng:
\({S_q} =\dfrac {{\pi {R^2}n}}{ {360}}\)
Diện tích hình viên phân: \(S = {S_q} - {S_{AOB}}\)
Lời giải chi tiết
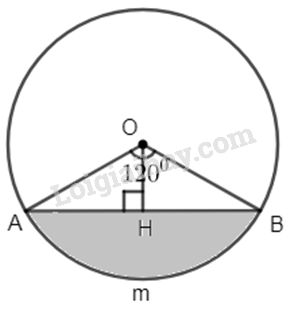
Kẻ đường cao OH.
Ta có \(\widehat {AOB} = 120^\circ \Rightarrow \widehat {OAB} = \widehat {OBA} = 30^\circ \) nên trong tam giác vuông AHO, ta có
\(OH = \dfrac{R }{ 2}\) và \(AH = \dfrac{{R\sqrt 3 } }{2} \Rightarrow AB = R\sqrt 3 \).
Vậy \(S_{AOB}=\dfrac{1 }{2}AB.OH =\dfrac {1 }{ 2}R\sqrt 3 .\dfrac{R }{2} \)\(\,= \dfrac{{{R^2}\sqrt 3 }}{ 4}\) (đvdt)
\({S_q} =\dfrac {{\pi {R^2}n}}{ {360}} =\dfrac {{\pi {R^2}.120} }{ {360}} =\dfrac {{\pi {R^2}} }{ 3}\) (đvdt)
Do đó : \(S = {S_q} - {S_{AOB}} = \dfrac{{\pi {R^2}}}{ 3} - \dfrac{{{R^2}\sqrt 3 }}{4}\)\(\, = \dfrac{{{R^2}\left( {4\pi - 3\sqrt 3 } \right)} }{ {12}}\) (đvdt).
soanvan.me
