Đề bài
Cho tam giác ABC đồng dạng với tam giác MNP với tỉ số đồng dạng \(k = {2 \over 3}\) . Kẻ đường cao AH của tam giác ABC và đường cao MK của tam giác MNP.
a) Chứng minh tam giác ABH đồng dạng với tam giác MNK.
b) Biết diện tích tam giác ABC bằng 56 cm2. Tính diện tích tam giác MNK.
Lời giải chi tiết
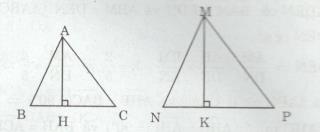
a) Xét ∆ABH và ∆MNK có: \(\widehat B = \widehat N(\Delta ABC \sim \Delta MNP)\) và \(\widehat {AHB} = \widehat {MKN}( = 90^\circ )\)
\(\eqalign{ & \Rightarrow \Delta ABH \sim \Delta MNK(g.g) \cr} \)
\(\eqalign{ & \cr & b)\Delta ABC \sim MNP(gt)\cr& \Rightarrow {{{S_{ABC}}} \over {{S_{MNP}}}} = {k^2} = {\left( {{2 \over 3}} \right)^2} = {4 \over 9}\cr& \Rightarrow {{56} \over {{S_{MNP}}}} = {4 \over 9}\cr& \Rightarrow {S_{MNP}} = {{56.9} \over 4} = 126(c{m^2}) \cr} \)
Vì tam giác \(MNK\) có chiều cao \(MK\) và đáy \(NK\) không cố định (nó còn phụ thuộc vào tam giác \(MNP\)) nên diện tích tam giác \(MNK\) không cố định, do đó trong bài toán này ta chưa đủ điều kiện để tính được diện tích tam giác \(MNK\).
soanvan.me
