Đề bài
Hãy tìm cặp tam giác đồng dạng trong các câu sau:
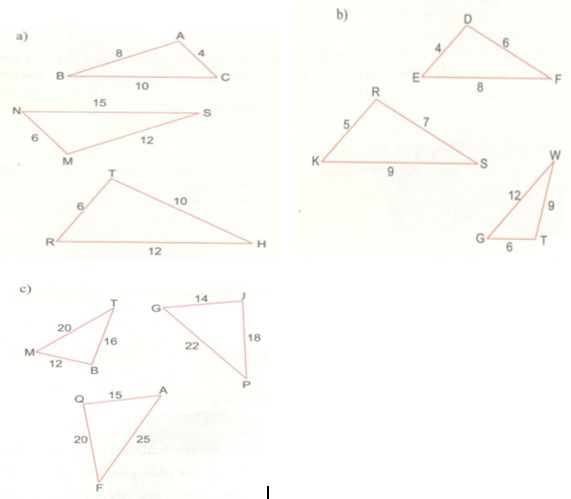
Lời giải chi tiết
a) Ta có
\(\dfrac{{AC}}{{NM}} = \dfrac{4}{6} = \dfrac{2}{3};\dfrac{{AB}}{{MS}} = \dfrac{8}{{12}} =\dfrac{2}{3};\)\(\;\dfrac{{BC}}{{NS}} = \dfrac{{10}}{{15}} = \dfrac{2}{3}\)
Xét ∆ABC và ∆MSN có: \({{AC} \over {NM}} = {{AB} \over {MS}} = {{BC} \over {NS}}\left( { = {2 \over 3}} \right) \)
\(\Rightarrow \Delta ABC \sim \Delta MSN(c.c.c)\)
\(b){{DE} \over {GT}} = {4 \over 6} = {2 \over 3};{{DF} \over {T{\rm{W}}}} = {6 \over 9} = {2 \over 3};\)\(\,{{EF} \over {G{\rm{W}}}} = {8 \over {12}} = {2 \over 3}\)
Xét ∆DEF và ∆TGW có: \({{DE} \over {GT}} = {{DF} \over {T{\rm{W}}}} = {{EF} \over {G{\rm{W}}}} \)
\(\Rightarrow \Delta DEF \sim \Delta TGW(c.c.c)\)
c) \({{MB} \over {QA}} = {{12} \over {15}} = {4 \over 5};{{BT} \over {QF}} = {{16} \over {20}} = {4 \over 5};\)\(\,{{MT} \over {AF}} = {{20} \over {25}} = {4 \over 5}\)
Xét ∆MBT và ∆AQF có: \({{MB} \over {QA}} = {{BT} \over {QF}} = {{MT} \over {AF}} \)
\(\Rightarrow \Delta MBT \sim \Delta AQF(c.c.c)\)
soanvan.me
