Đề bài
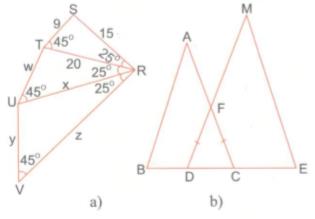
a) Trong hình a, hãy tính x, y, z, w.
b) Trong hình b, cho biết FD = FC, BC = 9 cm, DE = 12 cm, AC = 15 cm, MD = 20 cm. Chứng minh rằng tam giác ABC và tam giác MED đồng dạng với nhau.
Lời giải chi tiết
a) Xét ∆RUT và ∆RTS có: \(\widehat {TRU} = \widehat {SRT}( = 25^\circ ),\) \(\widehat {TUR} = \widehat {STR}( = 45^\circ )\)
\( \Rightarrow \Delta RUT \sim \Delta RTS(g.g)\)
\(\Rightarrow {{RU} \over {RT}} = {{RT} \over {RS}} = {{UT} \over {TS}}\)
\(\Rightarrow {x \over {20}} = {{20} \over {15}} = {{\rm{w}} \over 9}\)
Từ đó suy ra: \({x \over {20}} = {{20} \over {15}} \)
\(\Rightarrow x = {{400} \over {15}} = {{80} \over 3}\) và \({{20} \over {15}} = {{\rm{w}} \over 9} \Rightarrow {\rm{w}} = {{180} \over {15}} = 12\)
Xét ∆RVU và ∆RUT có \(\widehat {URV} = \widehat {TRU}( = 25^\circ ),\) \(\widehat {UVR} = \widehat {TUR}( = 45^\circ )\)
\( \Rightarrow \Delta RVU \sim \Delta RUT(g.g) \)
\(\Rightarrow {{RV} \over {RU}} = {{RU} \over {RT}} = {{VU} \over {UT}}\)
\(\Rightarrow {z \over {{{80} \over 3}}} = {{{{80} \over 3}} \over {20}} = {y \over {12}}\)
Từ đó suy ra:
•\({z \over {{{80} \over 3}}} = {{{{80} \over 3}} \over {20}} \Rightarrow 20z = {{6400} \over 9} \Rightarrow z = {{320} \over 9}\)
•\({{{{80} \over 3}} \over {20}} = {y \over {12}} \Rightarrow 20y = 320 \Rightarrow y = 16\)
Vậy x=\({{80} \over {13}},y = 16,z = {{320} \over 9},{\rm{w}} = 12\)
b) Ta có: FD = FC => ∆FDC cân tại F \( \Rightarrow \widehat {FDC} = \widehat {FCD} \Rightarrow \widehat {MDE} = \widehat {ACB}\)
Ta có: \({{BC} \over {DE}} = {9 \over {12}} = {3 \over 4};{{AC} \over {MD}} = {{15} \over {20}} = {3 \over 4}\)
Xét ∆ABC và ∆MED có: \({{BC} \over {DE}} = {{AC} \over {MD}}\left( { = {3 \over 4}} \right),\widehat {ACB} = \widehat {MDE}\)
\(\Rightarrow \Delta ABC \sim \Delta MED(c.g.c)\)
soanvan.me
