Đề bài
Cho tam giác ABC vông tại A có đường cao AH. Từ một điểm I trên AH kẻ đường thẳng song song cới BC cắt cạnh AB ở D, cắt AC ở E. Biết \({{AI} \over {AH}} = {1 \over 3}\)
a) Chứng minh rằng tam giác ADE đồng dạng với tam giác ABC.
b) Tính tỉ số đồng dạng của hai tam giác ADE và ABC.
c) Biết AB = 9 cm, AC = 12 cm. Tính diện tích tam giác ADE.
Lời giải chi tiết
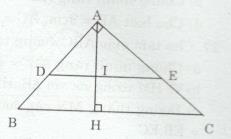
a) Xét ∆ADE và ∆ABC có: \(\widehat A\) (chung) và \(\widehat {ADE} = \widehat {ABC}\) (hai góc đồng vị và DE // BC)
\( \Rightarrow \Delta ADE \sim \Delta ABC(g.g)\)
b) ∆ABH có DI // BH (gt) \( \Rightarrow {{AD} \over {AB}} = {{AI} \over {AH}} = {1 \over 3}\) (định lý Thales)
\(\Delta ADE \sim \Delta ABC\) (câu a) \( \Rightarrow {{AD} \over {AB}} = {{AE} \over {AC}} = {{DE} \over {BC}} = {1 \over 3}\)
Tỉ số đồng dạng của hai tam giác là \({1 \over 3}\)
\(\eqalign{ & c){S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.9.12 = 54(c{m^2}) \cr & \Delta ADE \sim \Delta ABC\cr& \Rightarrow {{{S_{ADE}}} \over {{S_{ABC}}}} = {k^2} = {1 \over 9}\cr& \Rightarrow {{{S_{ADE}}} \over {54}} = {1 \over 9} \cr&\Rightarrow {S_{ADE}} = {1 \over 9}.54 = 6(c{m^2}) \cr} \)
soanvan.me
