Đề bài
Cho các số phức z1 = 1 + i; z2 = 1 – 2i. Hãy tính và biểu diễn hình học các số phức: \(z_1^2;{z_1}{z_2};2{z_1} - {z_2}:{z_1}\overline {z_2};{{{z_2}} \over {\overline {z_1}}}\)
Lời giải chi tiết
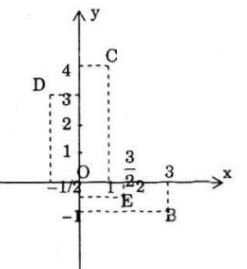
z12 = (1 + i)2 \( = 1 + 2i + {i^2} = 1 + 2i - 1\) = 2i
z1z2 = (1 + i)(1 – 2i) \( = 1 + i - 2i - 2{i^2} = 1 - i + 2\) = 3 – i
2z1 – z2 = 2(1 + i) – (1 – 2i)
=2-2i-1+2i = 1 + 4i
\({z_1}\overline {{z_2}} = (1 + i)(1 + 2i) \) \( = 1 + i + 2i + 2{i^2}\) \( = 1 + 3i - 2 = - 1 + 3i\)
\({{{z_2}} \over {\overline {z_1}}} = {{1 - 2i} \over {1 - i}} = {{(1 - 2i)(1 + i)} \over 2} \) \( = \frac{{1 - 2i + i - 2{i^2}}}{2} = \frac{{3 - i}}{2}= {3 \over 2} - {i \over 2}\)
soanvan.me
