Đề bài
Cho đường tròn (O; R) và một điểm A sao cho \(OA = 2R.\) Vẽ các tiếp tuyến AB, AC (B, C là các tiếp điểm). Đường thẳng OA cắt BC tại H, cắt cung nhỏ và cung lớn BC lần lượt tại M và N.
a. Chứng minh rằng: \(OA ⊥ BC\) và \({R^2} = OA.HM\)
b. Vẽ cát tuyến bất kì ADE. Gọi K là trung điểm của DE. Chứng tỏ năm điểm A, B, O, K, C thuộc cùng một đường tròn.
Phương pháp giải - Xem chi tiết
a.+Dựa vào tính chất hai tiếp tuyến cắt nhau ta chứng minh được OA là đường trung trực của BC
+Từ OA=2R ta có M là trung điểm của OA, do đó ta chứng minh được MH=HO suy ra đpcm
b.Sử dụng:
+Đường kính đi qua trung điểm của dây cung thì vuông góc với dây ấy
+Trong tam giác vuông đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền
Lời giải chi tiết
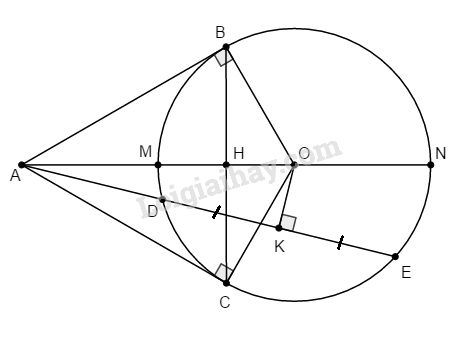
a. AB và AC là hai tiếp tuyến của đường tròn (O) ta có \(AB = AC\), lại có \(OB = OC (=R)\) nên OA là đường trung trực của đoạn BC \(⇒ OA ⊥ BC.\)
Ta có: \(OA = 2R (gt)\)
\(⇒ MA = OA - MO = 2R - R = R\)
Hay M là trung điểm của AO.
∆ABO có BM là trung tuyến nên:
\(BM = MO = {{AO} \over 2} = R\)
Vậy ∆BMO đều. Do đó đường cao BH cũng đồng thời là đường trung tuyến nên \(HM = HO = {R \over 2}\)
∆ABO vuông có BH là đường cao nên \(O{B^2} = OA.OH\) (hệ thức lượng)
hay \({R^2} = OA.HM\)
b. K là trung điểm của \(DE ⇒ OK ⊥ DE\) (định lí đường kính dây cung)
Do đó ∆AKO vuông tại K có OA là cạnh huyền, lại có các tam giác ABO, ACO vuông cũng có OA là cạnh huyền. Vì vậy năm điểm A, B, O, K, C thuộc cùng một đường tròn có đường kính OA.
soanvan.me
