Đề bài
Bài 1. Cho hàm số \(y = f\left( x \right) = - \sqrt 2 x.\) Tính : \(f\left( {\sqrt 2 } \right);f\left( { - \sqrt 2 } \right);f\left( {3\sqrt 2 } \right)\)
Bài 2. Chứng minh hàm số : \(y = f\left( x \right) = - 2x + 1\) nghịch biến trên R.
Bài 3. Vẽ đồ thị của hàm số : \(y = \sqrt 2 x\)
LG bài 1
Phương pháp giải:
Để tính giá trị \({y_0}\) của hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\) ta thay \(x = {x_0}\) vào \(f\left( x \right)\), ta được \({y_0} = f\left( {{x_0}} \right)\).
Lời giải chi tiết:
Ta có:
\(\eqalign{ & f\left( {\sqrt 2 } \right) = \left( { - \sqrt 2 } \right).\sqrt 2 = - 2 \cr & f\left( { - \sqrt 2 } \right) = {\left( { - \sqrt 2 } \right)^2} = 2 \cr & f\left( {3\sqrt 2 } \right) = \left( { - \sqrt 2 } \right).\left( {3\sqrt 2 } \right) = - 6 \cr} \)
LG bài 2
Phương pháp giải:
Giả sử \({x_1} < {x_2}\) và \({x_1},{x_2} \in \mathbb R\).
Xét hiệu \(H = f\left( {{x_1}} \right) - f\left( {{x_2}} \right)\).
+ Nếu \(H < 0\) thì hàm số đồng biến trên \(\mathbb R\)
+ Nếu \(H > 0\) thì hàm số nghịch biến trên \(\mathbb R\)
Lời giải chi tiết:
Với \({x_1},\,{x_2}\) bất kì thuộc \(\mathbb R\) và \({x_1}<{x_2}\).
Ta có:
\( f\left( {{x_1}} \right) = - 2x + 1;f\left( {{x_2}} \right) = - 2{x_2} + 1 \)
\(\Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \left( { - 2{x_1} + 1} \right)\)\(\, - \left( { - 2{x_2} + 1} \right) = - 2\left( {{x_1} - {x_2}} \right) \)
Vì \({x_1}<{x_2}\)
\(\eqalign{ & \Rightarrow {x_1} - {x_2} < 0 \Rightarrow - 2\left( {{x_1} - {x_2}} \right) > 0 \cr & \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0\cr& \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right) \cr} \)
Vậy hàm số đã cho nghịch biến trên \(\mathbb R\).
LG bài 3
Phương pháp giải:
Cách vẽ đồ thị của hàm số \(y = ax + b (a ≠ 0).\)
- Chọn điểm \(P(0; b)\) (trên trục \(Oy\)).
- Chọn điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) (trên trục \(Ox\)).
- Kẻ đường thẳng \(PQ\) ta được đồ thị của hàm số \(y=ax+b.\)
Lời giải chi tiết:
Bảng giá trị :
|
x |
0 |
1 |
|
y |
0 |
\(\sqrt 2 \) |
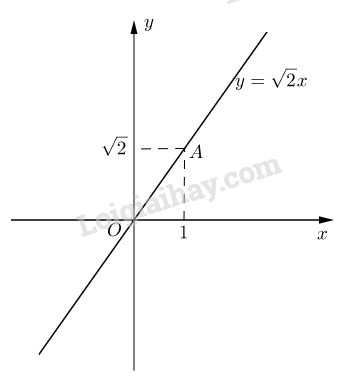
Đồ thị của hàm số là đường thẳng qua hai điểm : \(O(0; 0)\) và \(A(1; \sqrt 2 \)).
(Cách tìm điểm A. Ta dựng hình vuông OCBD có cạnh 1cm thì \(OB = \sqrt 2 \) . Dựng đường tròn tâm O, bán kính OB cắt Oy tại P \( \Rightarrow OP = \sqrt 2 \), từ đó tìm được \( A\left( {1;\sqrt 2 } \right)\))
soanvan.me
