Đề bài
Bài 1: Cho hai hàm số : \(y = {x^2}\) và \(y = 2x – 1.\)
a) Vẽ đồ thị (P) và (d) của hai hàm số trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) ( nếu có).
Bài 2: Cho hàm số \(y = f\left( x \right) = \left( {{m^2} - 2m + 3} \right){x^2}\). Chứng tỏ hàm số đồng biến khi \(x > 0\), từ đó hãy so sánh \(f\left( {\sqrt 2 } \right)\) và \(f\left( {\sqrt 5 } \right).\)
LG bài 1
Phương pháp giải:
a.Các bước vẽ đồ thị:
+Tìm tập xác định của hàm số.
+Lập bảng giá trị (thường từ 5 đến 7 giá trị) tương ứng giữa x và y.
+Vẽ đồ thị
b.
Giải phương trình hoành độ giao điểm của (d) và (P) ta tìm được x, từ đó thay vào (d) ta tìm được y
=>Tọa độ giao điểm
Lời giải chi tiết:
Bài 1: a)
TXĐ:\(x \in \mathbb{R}\)
Bảng giá trị \(( y = x^2)\)
|
x |
− 2 |
− 1 |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Đồ thị của hàm số là một parabol (P).
- Bảng giá trị \(( y = 2x – 1)\)
|
x |
0 |
1 |
|
y |
− 1 |
1 |
Đồ thị của hàm số là đường thẳng (d) qua hai điểm \(( 0; − 1), (1; 1).\)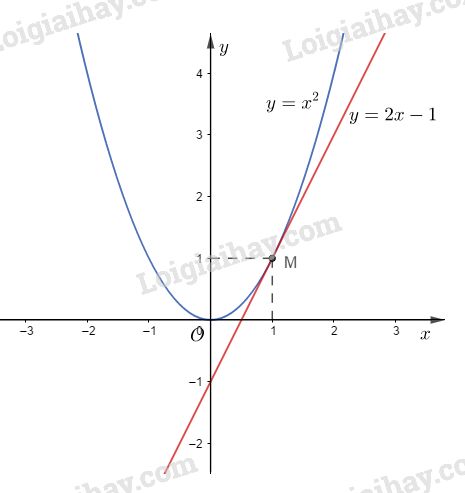
b) Phương trình hoành độ giao điểm của (P) và (d) :
\({x^2} = 2x - 1 \Leftrightarrow {x^2} - 2x + 1 = 0 \)
\(\Leftrightarrow {\left( {x - 1} \right)^2} = 0 \Leftrightarrow x = 1\)
Vậy tọa độ giao điểm của (P) và (d) là \(M(1; 1).\)
LG bài 2
Phương pháp giải:
+Chứng minh hệ số a>0 suy ra đpcm
+Sử dụng \(a < b \Leftrightarrow f\left( a \right) < f\left( b \right)\)
Lời giải chi tiết:
Bài 2: Ta có : \({m^2} - 2m + 3 = {m^2} - 2m + 1 + 2\)\(\;={\left( {m - 1} \right)^2} + 2 > 0\), với mọi m ( vì \(( m – 1)^2≥ 0)\)
Vậy hệ số \(a > 0\), với mọi m nên hàm số đã cho đồng biến khi \(x > 0.\)
Ta có : \(0 < \sqrt 2 < \sqrt 5 \Rightarrow f\left( {\sqrt 2 } \right) < f\left( {\sqrt 5 } \right).\)
soanvan.me
