Đề bài
Cho \(∆ABC\) cân tại A có \(AB = AC = 50cm, BC = 60cm\). Các đường cao AD và CE cắt nhau tại H. Tính CH.
Phương pháp giải - Xem chi tiết
Sử dụng định lý Pytago và tam giác đồng dạng.
Cho tam giác \(ABC\) vuông tại \(A\) ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago).
Lời giải chi tiết
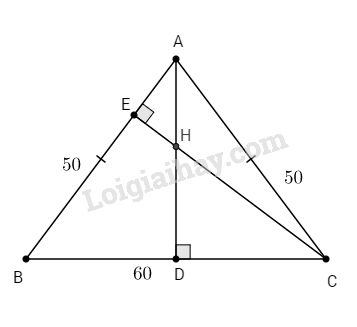
Ta có: \(∆ABC\) cân tại A nên đường cao AD đồng thời là đường trung tuyến:
\(DB = DC = {{BC} \over 2} = {{60} \over 2} = 30\,\left( {cm} \right)\)
Xét \(∆ADB\) có:
\(A{D^2} = A{B^2} - D{B^2}\) (định lí Pi-ta-go)
\( \Rightarrow AD = \sqrt {A{B^2} - D{B^2}} \)\(\;= \sqrt {{{50}^2} - {{30}^2}} = 40\,(cm)\)
Lại có: \( {S_{ABC}} = {1 \over 2}BC.AD = {1 \over 2}AB.CE \)
\(\Rightarrow CE = {{BC.AD} \over {AB}} = {{60.40} \over {50}} = 48\,\left( {cm} \right) \)
Ta có: \(∆CDH\) đồng dạng \(∆CEB\) (g.g) (do hai tam giác vuông có góc nhọn C chung)
\( \Rightarrow {{CH} \over {CB}} = {{DC} \over {CE}}\)
\(\Rightarrow CH = {{CB.DC} \over {CE}} = {{60.30} \over {48}} = 37,5\,\left( {cm} \right)\)
soanvan.me
