Đề bài
Xét hình 1. Hãy chứng minh hệ thức (3) (là \(bc=ah)\) bằng tam giác đồng dạng.
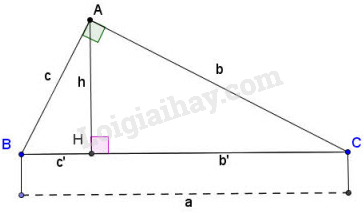
Hình 1
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng trường hợp đồng dạng g-g rồi suy ra tỉ lệ cạnh và hệ thức cần tìm.
Lời giải chi tiết
Cách 1:
Xét tam giác \(AHB\) và \(CAB\) có
\(\widehat{AHB}=\widehat{CAB}(=90^0\))
\(\widehat {B}\) chung
\( \Rightarrow \Delta ABH \backsim \Delta CBA\) (g-g)
\(\Rightarrow \dfrac{AB}{BC}=\dfrac {AH}{AC}\) ( cặp cạnh tương ứng tỉ lệ)
\(\Rightarrow AB.AC=AH.BC\) hay \(b.c=a.h\) (đpcm)
Cách 2:
Xét tam giác \(ABC\) vuông tại \(A\) có: \(S_{ABC}=\dfrac{1}2.AB.AC\) (1)
Xét tam giác \(ABC\) có chiều cao \(AH\) ứng với cạnh đáy \(BC\) có: \(S_{ABC}=\dfrac{1}2.AH.BC\) (2)
Từ (1) và (2) suy ra: \(AB.BC=AH.BC\) hay \(b.c=a.h\)
