Hình vuông là tứ giác có
-
A
Có bốn cạnh bằng nhau
-
B
Có bốn góc bằng nhau
-
C
Có bốn góc vuông và bốn cạnh bằng nhau
-
D
Cả A,B,C đều sai
Đáp án của giáo viên lời giải hay : C
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Khẳng định nào sau đây là sai?
-
A
Hình vuông vừa là hình thoi vừa là hình chữ nhật.
-
B
Hình vuông là hình chữ nhật nhưng không là hình thoi
-
C
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau
-
D
Hình vuông có đường chéo là phân giác các góc trong của hình vuông.
Đáp án của giáo viên lời giải hay : B
Hình vuông vừa là hình chữ nhật và hình thoi nên nó có đầy đủ tính chất của hình chữ nhật và hình thoi.
Từ đó A, C, D đúng, B sai.
Hãy chọn câu đúng. Cho hình vẽ. Tứ giác là hình vuông theo dấu hiệu:
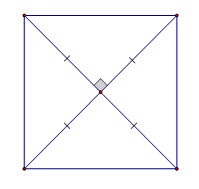
-
A
Hình thoi có một góc vuông
-
B
Tứ giác có hai đường chéo bằng nhau
-
C
Hình bình hành có hai đường chéo bằng nhau
-
D
Hình thoi có hai đường chéo bằng nhau
Đáp án của giáo viên lời giải hay : D
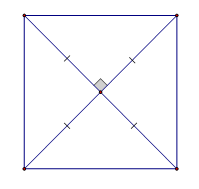
Từ hình vẽ ta thấy hai đường chéo của tứ giác vuông góc và giao nhau tại trung điểm mỗi đường nên nó là hình thoi.
Hình thoi này có hai đường chéo bằng nhau nên nó là hình vuông.
Chọn câu trả lời đúng. Tứ giác nào có hai đường chéo vuông góc với nhau?
-
A
Hình thoi
-
B
Hình vuông
-
C
Hình chữ nhật
-
D
Cả A và B.
Đáp án của giáo viên lời giải hay : D
+ Hình thoi và hình vuông đều có hai đường chéo vuông góc với nhau.
Cho hình vuông $ABCD$ . Trên các cạnh $AB,BC,CD,DA$ lần lượt lấy các điểm $E,F,G,H$ sao cho $AE = BF = CG = DH$ . Tứ giác \(EFGH\) là hình gì?
-
A
Hình chữ nhật
-
B
Hình thoi
-
C
Hình bình hành
-
D
Hình vuông
Đáp án của giáo viên lời giải hay : D
Bước 1: Ta chứng minh \(DG = CF = EB = AH\). Từ đó suy ra \(\Delta AHE = \Delta DGH = \Delta CFG = \Delta EBF\) nên \(HG = GF = HE = EF\) . Do đó tứ giác \(EFGH\) là hình thoi.
Bước 2: Chứng minh góc \(\widehat {HEF} = 90^\circ \) để suy ra \(EFGH\) là hình vuông.
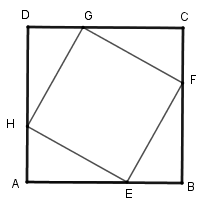
+ Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\) (tính chất).
Mà $AE = BF = CG = DH\,\left( {gt} \right)$ nên \(AB - AE = BC - BF = CD - CG = DA - DH\) hay \(DG = CF = EB = AH\).
Từ đó suy ra \(\Delta AHE = \Delta DGH = \Delta CFG = \Delta EBF\) (c-g-c) nên \(HG = GF = HE = EF\).
Vì \(HG = GF = HE = EF\) nên tứ giác \(EFGH\) là hình thoi.
+ Vì \(\Delta AHE = \Delta BEF\,\left( {cmt} \right) \Rightarrow \widehat {AHE} = \widehat {BEF}\) (hai góc tương ứng) mà \(\widehat {AHE} + \widehat {HEA} = 90^\circ \Rightarrow \widehat {BEF} + \widehat {HEA} = 90^\circ \)
Từ đó \(\widehat {HEF} = 180^\circ - \left( {\widehat {HEA} + \widehat {BEF}} \right) = 180^\circ - 90^\circ = 90^\circ \) .
Hình thoi \(EFGH\) có \(\widehat {HEF} = 90^\circ \) nên \(EFGH\) là hình vuông.
Cho hình vuông có chu vi \(28\,cm\) . Độ dài cạnh hình vuông là:
-
A
\(4\,cm\)
-
B
\(7\,cm\)
-
C
\(14\,cm\)
-
D
\(8\,cm\)
Đáp án của giáo viên lời giải hay : B
Hình vuông có bốn cạnh bằng nhau nên chu vi hình vuông bằng \(4a\) . (\(a\) là độ dài một cạnh)
Từ giả thiết ta có \(4a = 28 \Leftrightarrow a = 7\,cm\) . Vậy cạnh hình vuông là \(a = 7\,cm\) .
Cho hình vuông có chu vi \(16\,cm\) . Bình phương độ dài một đường chéo của hình vuông là:
-
A
\(32\)
-
B
\(16\)
-
C
\(24\)
-
D
\(18\)
Đáp án của giáo viên lời giải hay : A
Bước 1: Tính độ dài cạnh của hình vuông.
Bước 2: Sử dụng định lý Pytago để tính bình phương độ dài đường chéo.
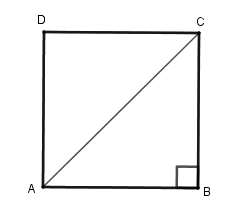
Gọi hình vuông \(ABCD\) có chu vi là \(16\,cm\) . Khi đó \(4.AB = 16\,cm \Rightarrow AB = 4cm = AB = CD = DA\) .
Xét tam giác $ABC$ vuông tại \(B\), theo định lý Pytago ta có \(A{B^2} + B{C^2} = A{C^2} \Rightarrow A{C^2} = {4^2} + {4^2} \Leftrightarrow A{C^2} = 32\) .
Vậy bình phương độ dài một đường chéo là \(32\) .
Cho tứ giác $ABCD.$ Gọi $E,F,G,H$ theo thứ tự là trung điểm của $AB,BC,CD,DA$ . Tìm điều kiện của tứ giác $ABCD$ để hình bình hành $EFGH$ là hình vuông.
-
A
\(BD \bot AC;BD = AC\)
-
B
\(BD \bot AC\)
-
C
\(BD = AC\)
-
D
\(AC = BD\) và \(AB{\rm{//}}CD\)
Đáp án của giáo viên lời giải hay : A
Dựa vào hai dấu hiệu nhận biết:
+ Hình bình hành có một góc vuông là hình chữ nhật
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
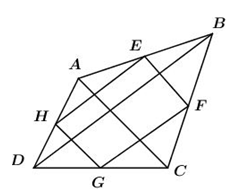
Ta có \(EH;\,EF\) lần lượt là đường trung bình của tam giác \(ABD;\,BAC\) nên
\(\left\{ \begin{array}{l}EH//BD;\,\,\,EF//AC\\EH = \dfrac{1}{2}BD;\,\,EF = \dfrac{1}{2}AC\end{array} \right.\,\,\left( 1 \right)\)
Hình bình hành EFGH là hình vuông khi và chỉ khi\(\left\{ \begin{array}{l}EH \bot EF\\EH = EF\end{array} \right.\,\left( 2 \right)\)
Từ \(\left( 1 \right);\,\left( 2 \right) \Rightarrow \left\{ \begin{array}{l}BD \bot AC\\DB = AC\end{array} \right.\) thì hình bình hành $EFGH$ là hình vuông.
Cho hình vuông $ABCD$ . $M,N,P,Q$ là trung điểm các cạnh $AB,BC,CD,DA$ . Hãy chọn câu đúng.
-
A
\({S_{MNPQ}} = \dfrac{1}{3}{S_{ABCD}}\)
-
B
\({S_{MNPQ}} = \dfrac{1}{4}{S_{ABCD}}\)
-
C
\({S_{MNPQ}} = \dfrac{1}{2}{S_{ABCD}}\)
-
D
\({S_{MNPQ}} = \dfrac{2}{3}{S_{ABCD}}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng công thức tính diện tích tam giác và diện tích hình vuông để tính diện tích \(MNPQ\)\({S_{MNPQ}} = {S_{ABCD}} - {S_{AMQ}} - {S_{MBN}} - {S_{CPN}} - {S_{DPQ}}\)
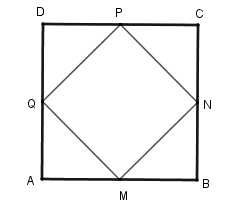
Gọi cạnh của hình vuông $ABCD$ là \(a\) .
Vì \(ABCD\) là hình vuông và $M,N,P,Q$ là trung điểm các cạnh$AB,BC,CD,CA$ nên ta có \(AM = MB = BN = NC = CP = PD = DQ = QA = \dfrac{a}{2}.\)Từ đó \(\Delta AQM = \Delta BMN = \Delta CPN = \Delta DQP\,\left( {c - g - c} \right)\)
Suy ra \({S_{QAM}} = {S_{MNB}} = {S_{CPN}} = {S_{DPQ}} = \dfrac{{DQ.DP}}{2}\)\( =\dfrac{{\dfrac{a}{2}.\dfrac{a}{2}}}{2} = \dfrac{{{a^2}}}{{4.2}}= \dfrac{{{a^2}}}{8}.\) Lại có \({S_{ABCD}} = {a^2}.\)
Nên \({S_{MNPQ}} = {S_{ABCD}} - {S_{AMQ}} - {S_{MBN}} - {S_{CPN}} - {S_{DPQ}}\)\( = {a^2} - 4.\dfrac{{{a^2}}}{8} = \dfrac{1}{2}{a^2} = \dfrac{1}{2}.{S_{ABCD}}.\)
Vậy \({S_{MNPQ}} = \dfrac{1}{2}{S_{ABCD}}\).
Cho tam giác $ABC$ vuông tại $A$ . Gọi $M,N,P$ lần lượt là các trung điểm của $AB,BC,AC$ . Tam giác $ABC$ cần có thêm điều kiện gì để hình chữ nhật $AMNP$ là hình vuông?
-
A
\(AB = \dfrac{1}{2}AC\)
-
B
\(AB = AC\)
-
C
\(AC = \dfrac{1}{2}AB\)
-
D
\(\widehat B = 60^\circ \)
Đáp án của giáo viên lời giải hay : B
Sử dụng dấu hiệu nhận biết: “Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.”
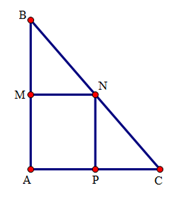
Hình chữ nhật $AMNP$ là hình vuông \( \Leftrightarrow AM = AP\) .
Mà \(AM = \dfrac{1}{2}AB;AP = \dfrac{1}{2}AC(gt)\) nên \(AM = AP \Leftrightarrow AB = AC\) .
Vậy nếu tam giác $ABC$ vuông cân tại $A$ thì hình chữ nhật $AMNP$ là hình vuông.
Cho tam giác $ABC$ vuông cân tại $A$. Trên cạnh $BC$ lấy các điểm $H,G$ sao cho \(BH = HG = GC\) . Qua $H$ và $G$ kẻ các đường vuông góc với $BC$ , chúng cắt $AB$ và $AC$ theo thứ tự tại $E$ và $F.$
Tứ giác $EFGH$ là hình gì?
-
A
Hình chữ nhật
-
B
Hình thoi
-
C
Hình bình hành
-
D
Hình vuông
Đáp án của giáo viên lời giải hay : D
Bước 1: Chứng minh tứ giác $EFGH$ là hình bình hành thông qua dấu hiệu nhận biết: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Bước 2: Chứng minh tứ giác $EFGH$ là hình chữ nhật thông qua dấu hiệu nhận biết: Hình bình hành có một góc vuông là hình chữ nhật.
Bước 3: Chứng minh tứ giác $EFGH$ là hình vuông thông qua dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
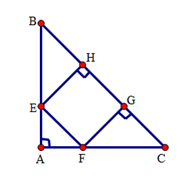
Ta có: \(\Delta ABC\) vuông cân tại $A$ nên \(\widehat B = \widehat C = \dfrac{{180^\circ - \widehat A}}{2} = \dfrac{{180^\circ - 90^\circ }}{2} = 45^\circ \)
Xét tam giác vuông $FGC$ có
\(\widehat {GFC} = 180^\circ - \widehat {FGC} - \widehat C = 180^\circ - 90^\circ - 45^\circ = 45^\circ \) \( \Rightarrow \widehat {GFC} = \widehat C\)
Suy ra \(\Delta FGC\) là tam giác vuông cân tại $G$ \( \Rightarrow FG = GC\)
Chứng minh tương tự:
Xét tam giác vuông $EHB$ có
\(\widehat {BEH} = 180^\circ - \widehat {EHB} - \widehat B = 180^\circ - 90^\circ - 45^\circ = 45^\circ \)\( \Rightarrow \widehat {BEH} = \widehat B\)
Suy ra tam giác $EBH$ vuông cân tại $H$ \( \Rightarrow EH = HB\)
Mà \(BH = HG = GC(gt)\) nên \(FG = EH = HG\)
Lại có: $\left. \begin{array}{l}EH \bot BC(gt)\\FG \bot BC(gt)\end{array} \right\} \Rightarrow EH{\rm{//}}FG$ ( định lí từ vuông góc đến song song)
Xét tứ giác $EFGH$ có:
\(\left\{ \begin{array}{l}EH = FG(cmt)\\EH{\rm{//}}FG(cmt)\end{array} \right.\) \( \Rightarrow \) Tứ giác $EFGH$ là hình bình hành (dhnb)
Mà \(\widehat H = 90^\circ \) ( do \(EH \bot BC\) ) nên hình bình hành $EFGH$ là hình chữ nhật.
Mặt khác \(EH = HG(cmt)\) nên hình chữ nhật $EFGH$ là hình vuông.
Cho \(BC = 9cm\) . Tính chu vi của tứ giác $EFGH$ .
-
A
\(12\,cm\)
-
B
\(9\,cm\)
-
C
\(16\,cm\)
-
D
\(20\,cm\)
Đáp án của giáo viên lời giải hay : A
Bước 1: Tính cạnh \(HG\) của hình vuông \(EFGH\) .
Bước 2: Chu vi \(EFGH\) bằng \(4.HG\) .
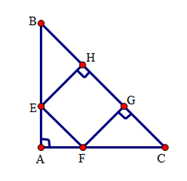
Vì \(FG = EH = HG\) nên \(HG = \dfrac{{BC}}{3} = \dfrac{9}{3} = 3cm\)
Do đó chu vi hình vuông \(EFGH\) là \(4.HG = 4.3 = \,12\,cm\) .
Cho tam giác $ABC$ cân tại $A$ , đường trung tuyến $AM.$ Gọi $I$ là trung điểm của $AC$ . $K$ là điểm đối xứng với $M$ qua điểm $I$ .
Tứ giác $AKMB$ là hình gì?
-
A
Hình chữ nhật
-
B
Hình thoi
-
C
Hình bình hành
-
D
Hình vuông
Đáp án của giáo viên lời giải hay : C
Bước 1: Chứng minh $AMCK$ là hình chữ nhật (hoặc hình bình hành) để suy ra \(AK = MC;\,AK{\rm{//}}MC\) .
Bước 2: Sử dụng dấu hiệu nhận biết: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành
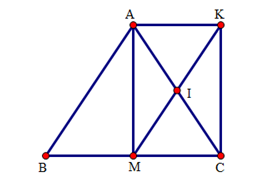
+ Tam giác $ABC$ cân tại$A$ , $AM$ là đường trung tuyến nên $AM$ đồng thời là đường cao.
\( \Rightarrow AM \bot BC \Rightarrow \widehat {AMC} = 90^\circ \)
Xét tứ giác $AMCK$ có:
\(\left\{ \begin{array}{l}AI = IC(gt)\\MI = IK(gt)\\AC \cap MK = I\,(gt)\end{array} \right.\)
Suy ra tứ giác $AMCK$ là hình bình hành (dhnb).
Lại có: \(\widehat {AMC} = 90^\circ (cmt)\) nên hình bình hành $AMCK$ là hình chữ nhật.
+ Ta có:
\(AK{\rm{//}}MC\) ( do $AMCK$ là hình chữ nhật), \(M \in BC(gt) \Rightarrow AK{\rm{//}}BM\)
Mà \(BM = MC\) ( do $AM$ là trung tuyến), \(AK = MC\) (do $AMCK$ là hình chữ nhật) nên \(AK = BM\) (tính chất bắc cầu)
Xét tứ giác $ABMK$ có:
\(\left\{ \begin{array}{l}AK = BM(cmt)\\AK{\rm{//}}BM(cmt)\end{array} \right.\)
Suy ra tứ giác $ABMK$ là hình bình hành.
Tìm điều kiện của tam giác $ABC$ để tứ giác $AMCK$ là hình vuông
-
A
Tam giác $ABC$ vuông cân tại $A$
-
B
Tam giác $ABC$ vuông cân tại $B$
-
C
Tam giác $ABC$ đều.
-
D
Tam giác $ABC$ vuông cân tại $C$.
Đáp án của giáo viên lời giải hay : A
Sử dụng dấu hiệu nhận biết hình chữ nhật có hai cạnh kề bằng nhau là hình vuông để tìm ra điều kiện tam giác $ABC$.
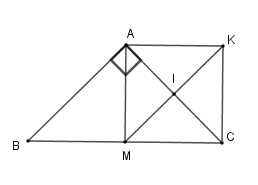
Hình chữ nhật $AMCK$ là hình vuông \( \Leftrightarrow AM = MC\)
Mà \(MC = \dfrac{1}{2}BC(gt)\) nên \(AM = MC \Leftrightarrow AM = \dfrac{1}{2}BC\)
Do $AM$ là đường trung tuyến của tam giác $ABC$ nên \(AM = \dfrac{1}{2}BC \Leftrightarrow \) tam giác $ABC$ vuông tại$A$ .
Vậy nếu tam giác $ABC$ vuông cân tại $A$ thì tứ giác $AMCK$ là hình vuông.
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chọn câu đúng.
-
A
\(AK + CE = BE\)
-
B
\(AK + CE = 2BE\)
-
C
\(AK + CE = \dfrac{{BE}}{2}\)
-
D
\(AK + CE > BE\)
Đáp án của giáo viên lời giải hay : A
Vẽ thêm điểm M trên tia đối của tia CD sao cho \(CM = AK\).
Sử dụng tính chất hai tam giác bằng nhau và tính chất tam giác cân.
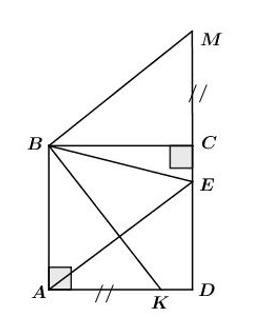
Trên tia đối của tia CD lấy điểm M sao cho \(CM = AK\) . Ta có: \(AK + CE = CM + CE = EM\) .
Ta cần chứng minh \(EM = BE\) .
Xét \(\Delta BAK\) và \(\Delta BCM\) có:
\(AK = CM\) ( cách vẽ)
\(\begin{array}{l}\widehat A = \widehat C = 90^\circ (gt)\\BA = BC(gt)\\ \Rightarrow \Delta BAK = \Delta BCM(c.g.c)\end{array}\)
\( \Rightarrow \widehat {ABK} = \widehat {CBM};\widehat {\,\,AKB} = \widehat {CMB}\) (góc tương ứng)
Mà \(\widehat {ABK} = \widehat {KBE}\) (gt) nên \(\widehat {KBE} = \widehat {CBM}\) (bắc cầu).
Ta có:
\(\widehat {EBM} = \widehat {EBC} + \widehat {CBM} = \widehat {EBC} + \widehat {KBE} = \widehat {KBC} = \widehat {AKB}(slt) = \widehat {CMB}\).
Suy ra: tam giác EBM cân tại E (định nghĩa tam giác cân).
\(\begin{array}{l} \Rightarrow BE = EM\\ \Rightarrow AK + CE = CM + CE = EM = BE\\ \Rightarrow AK + CE = BE\,\,\,\,\end{array}\).
