Chọn câu đúng.
-
A
Đường trung bình của hình thang là đường nối trung điểm hai cạnh đáy hình thang.
-
B
Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.
-
C
Trong một tam giác chỉ có một đường trung bình.
-
D
Đường trung bình của tam giác là đường nối từ một đỉnh đến trung điểm cạnh đối diện.
Đáp án của giáo viên lời giải hay : B
Ta sử dụng định nghĩa đường trung bình của tam giác và hình thang.
+ Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác nên B đúng.
+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang nên A, D sai.
+ Trong một tam giác có ba đường trung bình nên C sai.
Hãy chọn câu sai
-
A
Độ dài đường trung bình của hình thang bằng nửa tổng hai đáy.
-
B
Độ dài đường trung bình của hình thang bằng nửa hiệu hai đáy.
-
C
Đường trung bình của hình thang thì song song với hai đáy.
-
D
Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy.
Đáp án của giáo viên lời giải hay : B
Ta sử dụng định lý đường trung bình và hình thang
+ Độ dài đường trung bình hình thang bằng nửa tổng hai đáy nên đáp án B sai.
Hãy chọn câu đúng?
Cho tam giác \(ABC\) có chu vi là \(32\) cm. Gọi \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\). Chu vi của tam giác \(EFP\) là
-
A
\(17\,cm\).
-
B
\(33\,cm\).
-
C
\(15\,cm\).
-
D
\(16\,cm\).
Đáp án của giáo viên lời giải hay : D
Ta sử dụng định lý đường trung bình của tam giác để tìm mối liên hệ giữa chu vi tam giác \(ABC\) và chu vi tam giác \(EFP\) .
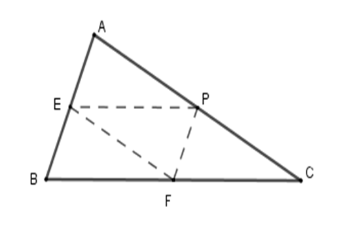
Vì \(E,F,P\) là trung điểm của các cạnh \(AB,BC,CA\) nên \(EF;EP;FP\) là các đường trung bình của tam giác \(ABC\) .
Suy ra \(EF = \dfrac{1}{2}AC;\,FP = \dfrac{1}{2}AB;\,EP = \dfrac{1}{2}BC\) \( \Rightarrow EF + FP + EP = \dfrac{1}{2}AC + \dfrac{1}{2}AB + \dfrac{1}{2}BC\)
\( \Leftrightarrow EF + FP + EP = \dfrac{1}{2}\left( {AB + AC + BC} \right)\) hay chu vi tam giác \(EFP = \dfrac{1}{2}\) chu vi tam giác \(ABC\) .
Do đó chu vi tam giác \(EFP\) là \(32:2 = 16\) cm .
Một hình thang có đáy lớn là \(5\,cm\), đáy nhỏ ngắn hơn đáy lớn là \(0,8\,cm\). Độ dài đường trung bình của hình thang là
-
A
\(4,7cm\).
-
B
\(4,8\,cm\).
-
C
\(4,6\,cm\).
-
D
\(5\,cm\).
Đáp án của giáo viên lời giải hay : C
Bước 1: Tính độ dài đáy nhỏ
Bước 2: Dựa vào định lý đường trung bình của hình thang để tính độ dài đường trung bình.
+ Vì đáy nhỏ ngắn hơn đáy lớn \(0,8\,cm\) nên độ dài đáy nhỏ là \(5 - 0,8 = 4,2\,cm\) .
+ Vì đường trung bình của hình thang bằng nửa tổng hai đáy nên độ dài đường trung bình là \(\dfrac{{5 + 4,2}}{2} = 4,6\,cm\) .
Hãy chọn câu đúng?
Cho \(\Delta ABC\), \(I,K\) lần lượt là trung điểm của \(AB\) và \(AC\). Biết \(BC = 8\,cm,AC = 7\,cm\). Ta có:
-
A
\(IK = 4\,cm\).
-
B
\(IK = 4,5\,cm\).
-
C
\(IK = 3,5\,cm\).
-
D
\(IK = 14\,cm\).
Đáp án của giáo viên lời giải hay : A
Ta sử dụng định lý đường trung bình của tam giác để tính độ dài.
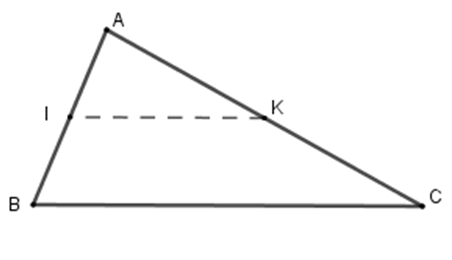
+ Vì \(I,K\) lần lượt là trung điểm của \(AB\) và \(AC\) nên \(IK\) là đường trung bình của tam giác \(ABC \)\(\Rightarrow IK = \dfrac{1}{2}BC = \dfrac{1}{2}.8 = 4\,cm\) .
Vậy \(IK = 4\,cm\) .
Cho \(\Delta ABC\) đều, cạnh \(2cm\); \(M,N\) là trung điểm của \(AB\) và \(AC\). Chu vi của tứ giác \(MNCB\) bằng
-
A
\(5cm\).
-
B
\(6cm\).
-
C
\(4cm\).
-
D
\(7cm\).
Đáp án của giáo viên lời giải hay : A
Bước 1: Ta sử dụng định lý đường trung bình của hình thang để tính độ dài cạnh \(MN\) .
Bước 2: Chu vi tứ giác \(MNCB\) là \(P = MN + BC + MB + NC\) .
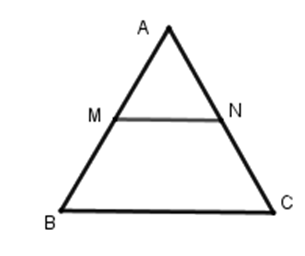
+ \(M,N\) là trung điểm của \(AB\) và \(AC\)nên \(MN\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow MN = \dfrac{1}{2}BC = \dfrac{1}{2}.2 = 1\,cm\) .
+ \(MB = \dfrac{{AB}}{2} = \dfrac{2}{2} = 1\,cm;\,NC = \dfrac{{AC}}{2} = \dfrac{2}{2} = 1\,cm\)
+ Chu vi tứ giác \(MNCB\) là \(P = MN + BC + MB + NC\)\( = 1 + 1 + 1 + 2 = 5\,cm\) .
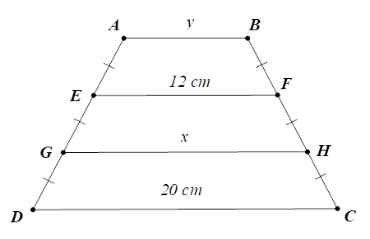
Tính \(x,y\) trên hình vẽ, trong đó \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\). Hãy chọn câu đúng.
-
A
\(x = 8cm,y = 16cm\).
-
B
\(x = 18cm,y = 9cm\).
-
C
\(x = 18cm,y = 8cm\).
-
D
\(x = 16cm,y = 8cm\).
Đáp án của giáo viên lời giải hay : D
Ta sử dụng định lý đường trung bình của hình thang để tính độ dài $x;\,y$.
+ Vì \(AB{\rm{//}}EF{\rm{//}}GH{\rm{//}}CD\) nên các tứ giác \(EFCD;\,ABHG\) là hình thang.
+ Từ hình vẽ ta có \(GH\) là đường trung bình của hình thang \(EFCD \Rightarrow HG = \dfrac{{EF + CD}}{2}\) \( = \dfrac{{12 + 20}}{2} = 16\,cm\) .
Hay \(x = 16\,cm\) .
+ Lại có \(EF\) là đường trung bình của hình thang \(ABHG \Rightarrow EF = \dfrac{{AB + HG}}{2}\)
\( \Rightarrow 12 = \dfrac{{AB + 16}}{2} \Rightarrow AB + 16 = 24 \Rightarrow AB = 8\,cm\) hay \(y = 8\,cm\) .
Vậy \(x = 16\,cm;\,y = 8\,cm\) .
Độ dài đường trung bình của hình thang là $16cm$; hai đáy tỉ lệ với $3$ và $5$ thì độ dài hai đáy là :
-
A
$12cm$ và $20cm$
-
B
$6cm$ và $10{\rm{ }}cm$
-
C
$3cm$ và $5cm$
-
D
Đáp số khác
Đáp án của giáo viên lời giải hay : A
Sử dụng định lí đường trung bình của hình thang và định lý dãy tỉ số bằng nhau.
Gọi $a$ và $b$ lần lượt là độ dài hai đáy nhỏ, đáy lớn của hình thang.
Theo định lí đường trung bình của hình thang suy ra \(a + b = 2.16 = 32(cm)\).
Mặt khác theo bài ra $a$ và $b$ tỉ lệ với $3$ và $5$ nên ta có: \(\dfrac{a}{3} = \dfrac{b}{5}\) .
Theo định lý của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3} = \dfrac{b}{5} = \dfrac{{a + b}}{{3 + 5}} = \dfrac{{32}}{8} = 4\) \( \Rightarrow a = 4.3 = 12(cm)\) và \(b = 4.5 = 20(cm)\).
Vậy độ dài $2$ đáy của hình thang là $12cm,{\rm{ }}20cm$ .
Cho tam giác $ABC$, đường trung tuyến $AM$. Gọi $D$ là trung điểm của $AM,E$ là giao điểm của $BD$ và $AC,F$ là trung điểm của $EC$. Chọn câu đúng trong các câu sau:
-
A
\(AE = \dfrac{1}{2}EC\)
-
B
$AE = 2EC$
-
C
$FC = AF$
-
D
$MF = BE$
Đáp án của giáo viên lời giải hay : A
Bước 1: Sử dụng các dấu hiệu nhận biết đường trung bình để chứng minh các đoạn thẳng là đường trung bình của tam giác.
Bước 2: Từ đó rút ra các mối liện hệ giữa các đoạn thẳng.
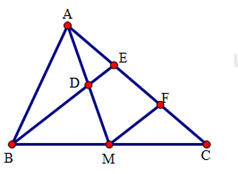
Xét tam giác $BEC$ có $BM = MC,EF = FC$ nên $MF$ là đường trung bình của tam giác $BEC$. Do đó $MF{\rm{//}}BE$.
Xét tam giác $AMF$ có $AD = DM,DE//MF$ nên $DE$ là đường trung bình của tam giác $AMF$. Do đó $AE = EF$.
Do đó $AE = EF = FC$ nên \(AE = \dfrac{1}{2}EC\).
Cho tam giác $ABC$, các đường trung tuyến $BD$ và $CE$ cắt nhau ở $G$. Gọi $I,K$ theo thứ tự là trung điểm của $GB,GC$. Trong các câu sau câu nào đúng?
-
A
$DE//IK$
-
B
$DE = IK$
-
C
Cả A và B đều đúng
-
D
Cả A và B đều sai.
Đáp án của giáo viên lời giải hay : C
Bước 1: Sử dụng dấu hiệu nhận biết để chứng minh các đường thẳng lần lượt là các đường trung bình của các tam giác tương ứng.
Bước 2: Sau đó sử dụng định lý của các đường trung bình để suy ra các mỗi liên hệ giữa các đoạn thẳng.
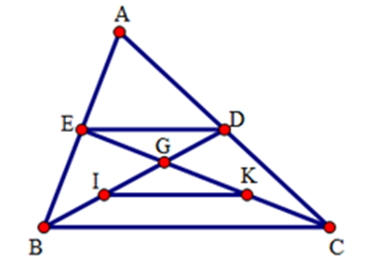
Vì tam giác $ABC$ có $AE = EB,AD = DC$ nên $ED$ là đường trung bình, do đó \(ED{\rm{//}}BC,ED = \dfrac{1}{2}BC\).
Tương tự tam giác $GBC$ có $GI = IB,GK = KC$ nên $IK$ là đường trung bình, do đó $IK{\rm{//}}BC,IK = \dfrac{1}{2}BC$.
Suy ra $ED{\rm{//}}IK$ (cùng song song với $BC$); $ED = IK$ (cùng bằng $\dfrac{1}{2}BC$).
Tính độ dài đường trung bình của hình thang cân, biết rằng hai đường chéo vuông góc với nhau và đường cao của nó bằng $10cm$ .
-
A
\(8\,cm\)
-
B
$5\,cm$
-
C
$6\,cm$
-
D
$10\,cm$
Đáp án của giáo viên lời giải hay : D
Ta đi chứng minh độ dài đường trung bình của hình thang cân \(ABCD\) bằng với độ dài đường cao đi qua giao điểm của hai đường chéo của hình thang. Từ đó suy ra độ dài đường trung bình của hình thang.
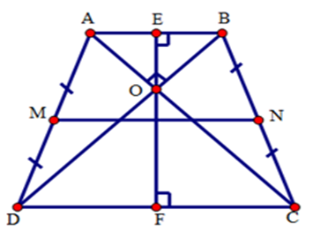
+ Xét hình thang cân $ABCD\left( {AB//CD} \right)$ , hai đường chéo $AC$ và $BD$ vuông góc với nhau tại $O,{\rm{ }}MN$ là đường trung bình của hình thang $ABCD$ . Qua $O$ kẻ đường thẳng vuông góc với $AB$ tại $E$ , với $CD$ tại $F$ .
Xét \(\Delta ADC\) và \(\Delta BCD\) có:
\(AD = BC\) (gt)
DC cạnh chung
\(\widehat {ADC} = \widehat {BCD}\) (gt)
\( \Rightarrow \Delta ADC = \Delta BCD(c.g.c) \Rightarrow \widehat {ACD} = \widehat {BDC}\) ( hai góc tương ứng)\( \Rightarrow \Delta OCD\) cân tại O\( \Rightarrow OC = OD\)
Mà \(AC = BD\) nên \(OA = OB \Rightarrow \Delta OAB\) cân tại $O$ .
Lại có \(\widehat {AOB} = 90^\circ \) ( do $AB$ vuông góc với $CD$) nên \(\Delta AOB\) vuông cân tại $O$, do đó $OE$ là đường cao cũng là đường trung tuyến nên \(OE = \dfrac{{AB}}{2}.\)
Tương tự: tam giác $DOC$ vuông cân tại $O$ nên $FO = \dfrac{{CD}}{2}$
Do đó \(FE = \dfrac{{AB + CD}}{2}\)
$MN$ là đường trung bình của hình thang $ABCD$ nên \(MN = \dfrac{{AB + CD}}{2}\)
\( \Rightarrow MN = FE = 10cm\) .
Cho tam giác $ABC$ , điểm $D$ thuộc cạnh $AC$ sao cho $AD = \dfrac{1}{2}DC$. Gọi $M$ là trung điểm của $BC,I$ là giao điểm của $BD$ và $AM$. So sánh \(AI\) và \(IM\) .
-
A
$AI = IM$
-
B
$AI > IM$
-
C
Cả A, B đều sai.
-
D
Chưa kết luận được.
Đáp án của giáo viên lời giải hay : A
Sử dụng dấu hiệu nhận biết để chứng minh các đoạn thẳng là đường trung bình của tam giác. Từ đó dùng các định lý của đường trung bình để suy ra điều cần chứng minh.
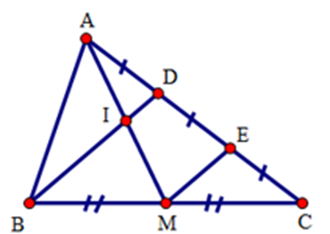
Gọi $E$ là trung điểm của $DC$ .
Xét tam giác $BDC$ có: $BM = MC,DE = EC$ nên $ME$ là đường trung bình của tam giác$BDC$ . Suy ra $BD//ME$ hay $DI//EM$ .
Xét tam giác $AME$ có $AD = DE,DI//EM$ nên $AI\; = IM$.
Tam giác \(ABC\) có \(AC = 2AB\), đường phân giác \(AD.\) Tính \(BD\) biết \(DC = 8cm.\)
-
A
\(BD = 4cm\)
-
B
\(BD = 5cm\)
-
C
\(BD = 3cm\)
-
D
\(BD = 8cm\)
Đáp án của giáo viên lời giải hay : A
+ Gọi \(M,E\) là trung điểm \(AC,DC\).
+ Sử dụng tính chất, định lý về đường trung bình của tam giác.
+ Sử dụng tính chất tam giác cân.
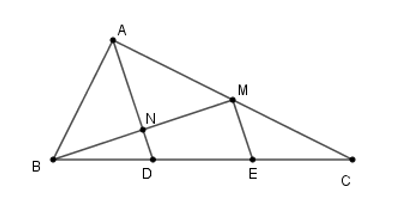
Gọi \(M,E\) lần lượt là trung điểm của \(AC,\,CD\).
Khi đó \(ME\) là đường trung bình của tam giác \(ACD \Rightarrow ME//AD\).
Gọi \(N\) là giao điểm của \(AD\) và \(BM.\)
Vì \(M\) là trung điểm của \(AC \Rightarrow AM = \dfrac{1}{2}AC\) mà \(AB = \dfrac{1}{2}AC\left( {gt} \right) \Rightarrow AB = AM\).
Suy ra tam giác \(ABM\) cân tại \(A\) có \(AN\) là phân giác (gt) nên \(AN\) cũng là đường trung tuyến của \(\Delta AMB\).
Hay \(NB = NM\)
Xét tam giác \(BME\) có \(NB = NM;\,ND//ME\) nên \(D\) là trung đểm của \(BE \Rightarrow BD = DE\).
Lại có: \(DE = \dfrac{1}{2}DC\) (do \(E\) là trung điểm \(DC\)) nên \(BD = \dfrac{1}{2}DC = \dfrac{1}{2}. 8 = 4cm.\)
Vậy \(BD = 4cm.\)
Tứ giác \(ABCD\) có \(E,F\) theo thứ tự là trung điểm của \(BD,AC.\) Gọi \(I\) là trung điểm của \(EF.\) Gọi \(M,N,P\) lần lượt là chân đường vuông góc kẻ từ \(A,B,I\) đến \(CD.\) Chọn câu đúng.
-
A
\(AM + BN = 2IP\)
-
B
\(AM + BN = 3IP\)
-
C
\(AM + BN = 4IP\)
-
D
\(AM + BN = 5IP\)
Đáp án của giáo viên lời giải hay : C
Gọi \(K,L\) lần lượt là chân đường vuông góc kẻ từ \(E,F\) đến \(DC\).
Sử dụng tính chất đường trung bình của tam giác và đường trung bình của hình thang.
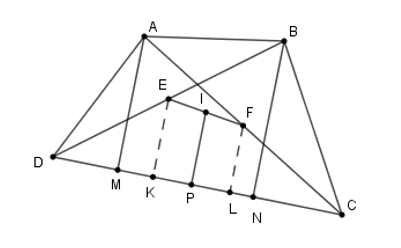
Gọi \(K,L\) lần lượt là chân đường vuông góc kẻ từ \(E,F\) đến \(DC\).
Suy ra \(AM//EK//IP//FL//BN\).
Xét tam giác \(ACM\) có \(F\) là trung điểm \(AC\) và \(FL//AM \Rightarrow L\) là trung điểm \(CM\)
Suy ra \(FL\) là đường trung bình của tam giác \(ACM \Rightarrow AM = 2FL\) (1)
Xét tam giác \(BDN\) có \(E\) là trung điểm \(BD\) và \(EK//NB \Rightarrow K\) là trung điểm \(DN\).
Suy ra \(EK\) là đường trung bình của tam giác \(BDN \Rightarrow BN = 2EK\) (2)
Xét tứ giác \(EKLF\) có \(EK//FL\) nên \(EKLF\) là hình thang.
Lại có: \(EK//IP//FL;\,IE = IF \Rightarrow PL = PK\).
Suy ra \(IP\) là đường trung bình của hình thang \(EFLK \Rightarrow EK + FL = 2IP\).
\( \Rightarrow 2EK + 2FL = 4IP\,\,\,\left( 3 \right)\)
Từ (1), (2), (3) suy ra \(AM + BN = 4IP\).
Cho hình thang \(ABCD\left( {AB//CD} \right)\), hai đường phân giác của góc \(A\) và góc \(D\) cắt nhau tại \(I\), hai đường phân giác của góc \(B\) và góc \(C\) cắt nhau tại \(J\). Gọi \(H\) là trung điểm của \(AD,{\rm{ }}K\) là trung điểm của \(BC\). Cho biết \(AB = AD = 10cm,BC = 12cm,CD = 20cm\). Tính độ dài các đoạn \(HI,{\rm{ }}IJ\) và \(JK\).
-
A
\(IH = 6\,cm;\,JK = 4\,cm;\,IJ = 5cm.\)
-
B
\(IH = 5\,cm;\,JK = 6cm;\,IJ = 4cm.\)
-
C
\(IH = 5\,cm;\,JK = 5cm;\,IJ = 4cm.\)
-
D
\(IH = 5\,cm;\,JK = 6cm;\,IJ = 6cm.\)
Đáp án của giáo viên lời giải hay : B
Sử dụng định lí đường trung bình của hình thang để tính \(HK\). Sau đó ta đi chứng minh bốn điểm \(H,I,J,K\) thẳng hàng từ đó tính được \(HI,IJ,IK\).
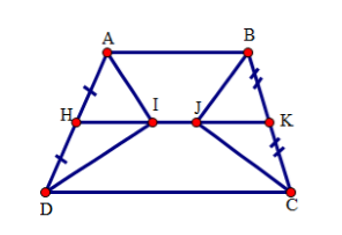
Xét hình thang \(ABCD\) có: \(H\) là trung điểm của \(AD,{\rm{ }}K\) là trung điểm của \(BC\) nên \(KH\) là đường trung bình của hình thang \(ABCD\).
Suy ra \(\left\{ \begin{array}{l}KH\parallel CD(1)\\HK = \dfrac{{AB + CD}}{2} = \dfrac{{10 + 20}}{2} = 15cm\end{array} \right.\)
Vì \(AI\) và \(DI\) là hai tia phân giác của góc \(A\) và góc \(D\) nên ta có:\(\widehat {IAD} + \widehat {IDA} = \dfrac{{\widehat A + \widehat D}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ \).
Xét \(\Delta AID\) có: \(\widehat {AID} = 180^\circ - \left( {\widehat {IAD} + \widehat {IDA}} \right) = 180^\circ - 90^\circ = 90^\circ \). Suy ra \(\Delta AID\) vuông tại \(I\).
Lại có \(IH\) là đường trung tuyến ứng với cạnh huyền \(AD\) của tam giác vuông \(AID\) nên \(HI = HD\).
Do đó tam giác \(HID\) cân tại \(H\) nên \(\widehat {HID} = \widehat {HDI}\).
Mà \(\widehat {HDI} = \widehat {IDC} \Rightarrow \widehat {HID} = \widehat {IDC} \Rightarrow HI\parallel DC(2)\).
Từ (1) và (2) suy ra \(H,{\rm{ }}I,{\rm{ }}K\) thẳng hàng hay điểm \(I\) thuộc đường thẳng \(HK\).
Tương tự điểm \(J\) thuộc đường thẳng \(HK\). Do đó bốn điểm \(H,{\rm{ }}I,{\rm{ }}J,{\rm{ }}K\) thẳng hàng.
\(\begin{array}{l}IH = \dfrac{{AD}}{2} = \dfrac{{10}}{2} = 5cm\\JK = \dfrac{{BC}}{2} = \dfrac{{12}}{2} = 6cm\\ \Rightarrow {\rm{IJ}} = HK - IH - JK = 15 - 5 - 6 = 4cm\end{array}\).
Vậy \(IH = 5\,cm;\,JK = 6cm;\,IJ = 4cm.\)
