Hãy chọn câu sai.
-
A
Hình thang là tứ giác có hai cạnh đối song song.
-
B
Nếu hình thang có hai cạnh bên song song thì tất cả các cạnh của hình thang bằng nhau.
-
C
Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên bằng nhau, hai cạnh bên song song
-
D
Hình thang vuông là hình thang có một góc vuông.
Đáp án của giáo viên lời giải hay : B
+ Hình thang là tứ giác có hai cạnh đối song song nên A đúng.
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau nên B sai vì cạnh bên và cạnh đáy chưa chắc bằng nhau.
+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau nên C đúng.
+ Hình thang vuông là hình thang có một góc vuông nên D đúng.
Chọn câu đúng nhất.
-
A
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
-
B
Trong hình thang cân, hai cạnh bên bằng nhau.
-
C
Trong hình thang cân, hai đường chéo bằng nhau.
-
D
Cả A, B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Vậy cả A, B, C đều đúng.
Hình thang $ABCD$ có \(\hat D = {80^0},\hat B = {50^0},\hat C = {100^0}\) . Số đo góc \(\widehat A\) là:
-
A
\({130^0}\)
-
B
\({140^0}\)
-
C
\({70^0}\)
-
D
\({120^0}\)
Đáp án của giáo viên lời giải hay : A
Ta sử dụng định lý về tổng các góc trong tứ giác.
Định lý: Tổng các góc của một tứ giác bằng \(360^\circ \) .
Vì tổng các góc của một tứ giác bằng \(360^\circ \) nên \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)\( \Rightarrow \widehat A = 360^\circ - 80^\circ - 50^\circ - 100^\circ = 130^\circ .\)
Góc kề cạnh bên của hình thang có số đo là\({70^0}\) . Góc kề còn lại của cạnh bên đó là
-
A
\({70^0}\)
-
B
\({120^0}\)
-
C
\({110^0}\)
-
D
\({180^0}\)
Đáp án của giáo viên lời giải hay : C
Ta sử dụng tính chất: Tổng hai góc kề cạnh bên của hình thang bằng \(180^\circ \) .
Vì tổng hai góc kề cạnh bên của hình thang bằng \(180^\circ \) nên góc kề còn lại của cạnh bên đó có số đo bằng \(180^\circ - 70^\circ = 110^\circ \) .
Cho tứ giác $ABCD$ có \(BC = CD\) và $DB$ là tia phân giác của góc \(D\). Chọn khẳng định đúng
-
A
\(ABCD\) là hình thang
-
B
\(ABCD\) là hình thang vuông
-
C
\(ABCD\) là hình thang cân
-
D
Cả A, B, C đều sai.
Đáp án của giáo viên lời giải hay : A
Chứng minh $AD{\rm{//}}BC$ suy ra \(ABCD\) là hình thang.
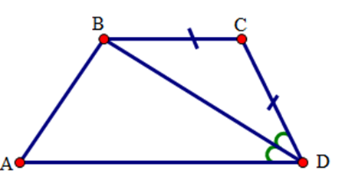
Xét \(\Delta BCD\) có \(BC = CD(gt)\) nên \(\Delta BCD\) là tam giác cân.
Suy ra \(\widehat {CBD} = \widehat {CDB}\)
Vì $DB$ là tia phân giác góc $D$ của tứ giác $ABCD$ nên \(\widehat {ADB} = \widehat {CDB}\)
Do đó \(\widehat {CBD} = \widehat {ADB}\)
Mà hai góc \(\widehat {CBD}\) và \(\widehat {ADB}\) là hai góc ở vị trí so le trong nên suy ra \(BC//AD\) .
Tứ giác $ABCD$ có $AD//BC$ (cmt) nên là hình thang.
Cho hình thang vuông $ABCD$ có \(\hat A = \hat D = 90^\circ ,\;AB = AD = 2cm,\;DC = 4cm.\) Tính góc \(ABC\) của hình thang.
-
A
$137^\circ $.
-
B
$136^\circ $.
-
C
$36^\circ $.
-
D
$135^\circ $.
Đáp án của giáo viên lời giải hay : D
Ta sử dụng tính chất hình thang, hình thang vuông và định lý về tổng các góc trong tứ giác.
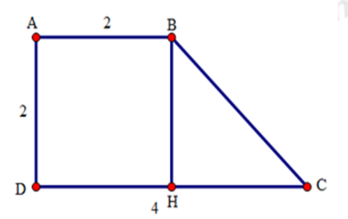
Từ $B$ kẻ $BH$ vuông góc với $CD$.
Tứ giác $ABHD$ là hình thang có hai cạnh bên \(AD{\rm{//}}BH\) nên \(AD = BH,AB = DH\) .
Mặt khác, \(AB = AD = 2cm\) nên suy ra \(BH = DH = 2cm\) .
Do đó: \(HC = DC - HD = 4 - 2 = 2cm\) .
Tam giác $BHC$ có \(BH = HC = 2cm\) nên tam giác $BHC$ cân đỉnh $H$.
Lại có \(\widehat {BHC} = 90^\circ \) (do $BH \bot CD$) nên tam giác $BHC$ vuông cân tại $H$.
Do đó \(\widehat {BCH} = \left( {180^\circ - \widehat {BHC}} \right):2 = \left( {180^\circ - 90^\circ } \right):2 = 45^\circ \)
Xét hình thang $ABCD$ có:
\(\widehat {ABC} = 360^\circ - \left( {\hat A + \hat D + \hat C} \right) = 360^\circ - \left( {90^\circ + 90^\circ + 45^\circ } \right) = 135^\circ .\)
Vậy \(\widehat {ABC} = 135^\circ \) .
Cho tam giác $ABC$ cân tại $A$. Gọi $D,E$ theo thứ tự thuộc các cạnh bên $AB,AC$ sao cho $AD{\rm{ }} = {\rm{ }}AE$ .
Tứ giác $BDEC$ là hình gì?
-
A
Hình thang
-
B
Hình thang vuông
-
C
Hình thang cân
-
D
Cả A, B, C đều sai.
Đáp án của giáo viên lời giải hay : C
Bước 1: Ta sử dụng tính chất tam giác cân để chứng minh hai góc đồng vị bằng nhau. Suy ra \(DE{\rm{//}}BC\) nên \(DECB\) là hình thang.
Bước 2: Sử dụng dấu hiệu nhận biết: Hình thang có hai góc ở đáy bằng nhau là hình thang cân để suy ra \(DECB\) là hình thang cân.
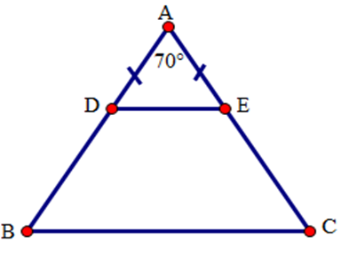
Tam giác $ADE$ có \(AD = AE(gt)\) nên tam giác $ADE$ cân tại $A$.
Suy ra \(\widehat {ADE} = \widehat {AED} = \left( {180^\circ - \widehat {DAE}} \right):2\;\left( 1 \right)\)
Tam giác $ABC$ cân tại $A$ (gt) nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {BAC}} \right):2\;\;\;\;\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\)
Mà 2 góc \(\widehat {ADE}\) và \(\widehat {ABC}\) là hai góc ở vị trí đồng vị nên suy ra $DE{\rm{//}}BC$
Tứ giác $BDEC$ có DE // BC nên tứ giác $BDEC$ là hình thang.
Lại có \(\widehat {ABC} = \widehat {ACB}\) (vì tam giác \(ABC\) cân tại \(A\) ) nên \(BDEC\) là hình thang cân.
Tính các góc của hình thang $BDEC$ , biết $\widehat A = {70^o}$ .
-
A
\(\widehat {BDE} = \widehat {DEC} = 125^\circ ;\,\widehat {DBC} = \widehat {ECB} = 55^\circ \).
-
B
\(\widehat {BDE} = \widehat {DEC} = 115^\circ ;\,\widehat {DBC} = \widehat {ECB} = 65^\circ \).
-
C
\(\widehat {BDE} = \widehat {DEC} = 55^\circ ;\,\widehat {DBC} = \widehat {ECB} = 125^\circ \).
-
D
\(\widehat {BDE} = \widehat {DEC} = 125^\circ ;\,\widehat {DBC} = \widehat {ECB} = 65^\circ \).
Đáp án của giáo viên lời giải hay : A
Ta sử dụng định lý về tổng các góc trong tam giác và tính chất về góc của hình thang cân.
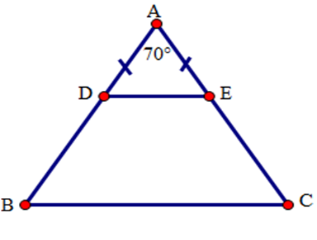
Ta có : \(\hat A = 70^\circ \)
Theo ý a) suy ra:
\(\widehat {ADE} = \widehat {AED} = \widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {DAE}} \right):2\;\)\( = (180^\circ - 70^\circ ):2 = 55^\circ \;\;\;\;\;\;\)
Vì \(\widehat {BDE}\) và \(\widehat {ADE}\) là hai góc kề bù nên \(\widehat {BDE} = 180^\circ - \widehat {ADE} = 180^\circ - 55^\circ = 125^\circ \)$ \Rightarrow \widehat {DEC} = 125^\circ $ (Vì $DEBC$ là hình thang cân)
Vậy \(\widehat {BDE} = \widehat {DEC} = 125^\circ ;\,\widehat {DBC} = \widehat {ECB} = 55^\circ \) .
Cho tam giác $ABC$. Các tia phân giác của các góc \(B\) và \(C\) cắt nhau tại \(I\). Qua \(I\) kẻ đường thẳng song song với $BC$, cắt các cạnh $AB,AC$ lần lượt tại $D$ và $E$.
Chọn khẳng định đúng nhất?
-
A
Tứ giác $BDIC$ là hình thang
-
B
Tứ giác $BIEC$ là hình thang
-
C
Tứ giác $BDEC$ là hình thang
-
D
Cả A, B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
Ta sử dụng định nghĩa hình thang: Tứ giác có hai cạnh đối song song là hình thang.
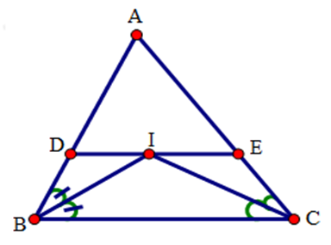
Xét tứ giác $DECB$ có: $DE//BC$ (gt) nên tứ giác $DECB$ là hình thang.
Tương tự :
Tứ giác $DICBS$ có $DI//BC$ (gt) nên tứ giác $DICB$ là hình thang
Tứ giác $IECB$ có $IE//CB$ (gt) nên tứ giác $IECB$ là hình thang.
Chọn khẳng định đúng.
-
A
\(DE > BD + CE\).
-
B
\(DE = BD + CE\).
-
C
\(DE < BD + CE\).
-
D
\(BC = BD + CE\).
Đáp án của giáo viên lời giải hay : B
Ta sử dụng tính chất các cạnh của tam giác cân.
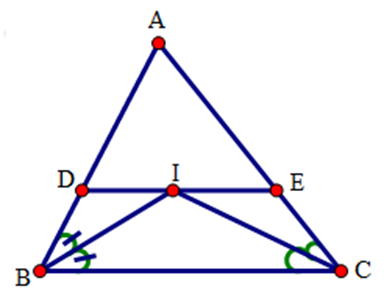
Vì $DE//BC$ (gt) nên suy ra \(\widehat {DIB} = \widehat {IBC}\) ( so le trong)
Mà \(\widehat {DBI} = \widehat {IBC}\) (gt) nên \(\widehat {DIB} = \widehat {DBI}\)
Suy ra tam giác $BDI$ cân đỉnh $D$.
Do đó \(DI = DB\,\,(1)\)
Ta có: $IE//CB$ nên suy ra \(\widehat {EIC} = \widehat {BCI}\) ( so le trong)
Mà \(\widehat {BCI} = \widehat {ECI}\) (gt) nên \(\widehat {ECI} = \widehat {EIC}\)
Suy ra tam giác $EIC$ cân đỉnh $E$.
Do đó \(EI = EC\,\,(2)\).
Cộng (1) và (2) vế theo vế ta được:
\(DI + EI = BD + CE \Rightarrow DE = BD + CE\)
Cho hình thang cân $MNPQ$ ($MN$ //$PQ$ ) có góc $\widehat {MQP} = {45^0}$ và hai đáy có độ dài$12cm$ ,$40cm$ . Diện tích của hình thang cân là:
-
A
$728\,c{m^2}$.
-
B
$346\,c{m^2}$.
-
C
$364\,c{m^2}$.
-
D
$362\,c{m^2}$.
Đáp án của giáo viên lời giải hay : C
Bước 1: Kẻ các đường cao \(MH,\,NK\) . Sử dụng tính chất về cạnh của hình thang cân để tính chiều cao hình thang
Bước 2: Áp dụng công thức diện tích \({S_{MNPQ}} = \dfrac{{\left( {MN + PQ} \right).MH}}{2}\)
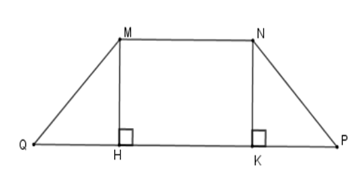
Kẻ \(MH \bot QP;\,NK \bot QP\) tại \(H,\,K \Rightarrow MH{\rm{//}}NK\)
Tứ giác \(MNHK\) có \(MN{\rm{//}}HK\) nên \(MNHK\) là hình thang , lại có \(MH{\rm{//}}NK \Rightarrow MN = HK;\,MH = NK\) .
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có \(MQ = NP\) (vì \(MNPQ\) là hình thang cân) suy ra \(\Delta MQH = \Delta NKP\,\left( {ch - cgv} \right)\)\( \Rightarrow QH = KP = \dfrac{{QP - HK}}{2}\)
Mà \(HK = MN = 12\,cm\) nên \(QH = KP = \dfrac{{40 - 12}}{2} = 14\,cm\).
Mà \(\widehat {MQP} = 45^\circ \Rightarrow \Delta MHQ\) vuông cân tại \(H \Rightarrow MH = QH = 14\,cm\) .
Diện tích hình thang cân \(MNPQ\) là \({S_{MNPQ}} = \dfrac{{\left( {MN + PQ} \right).MH}}{2} = \dfrac{{\left( {12 + 40} \right).14}}{2} = 364\,c{m^2}\) .
Cho hình thang cân $ABCD$ có đáy nhỏ$AB = 4\,cm$ , đường cao $AH = 6cm$ , và \(\widehat D = {45^ \circ }\). Độ dài đáy lớn $CD$ bằng
-
A
$12\,cm\;\;$
-
B
$16\,cm$
-
C
$18\,cm$
-
D
$20\,cm$
Đáp án của giáo viên lời giải hay : B
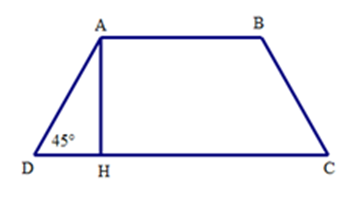
Ta có tam giác $ADH$ vuông cân tại $H$ vì $\widehat D = {45^ \circ }$. Do đó $DH = AH = 6cm$
Mà $DH = $\(\dfrac{1}{2}\left( {CD - AB} \right)\) . Suy ra $CD = 2DH + AB = 12 + 4 = 16\left( {cm} \right)$
Vậy $CD = 16cm$ .
Cho hình thang cân $ABCD$ đáy nhỏ $AB = 4cm$ , đáy lớn $CD = 10cm$ , cạnh bên $BC = 5cm$ thì đường cao $AH$ bằng:
-
A
$4,5cm\;$
-
B
$4cm$
-
C
$3,5cm$
-
D
$3cm$
Đáp án của giáo viên lời giải hay : B
Ta sử dụng tính chất hình thang cân và định lý Pytago.
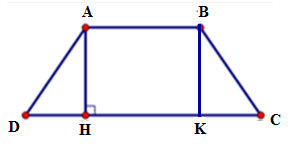
Kẻ $ BK \bot DC$ tại $K.$
Vì $ABCD$ là hình thang cân nên ta có \(\widehat D = \widehat C;AD = BC \Rightarrow \Delta AHD = \Delta BKC\left( {ch - gn} \right) \Rightarrow DH = CK\)
Suy ra \(DH = \dfrac{1}{2}\left( {CD - AB} \right)\)
Suy ra \(DH = \dfrac{1}{2}\left( {CD - AB} \right) = \dfrac{1}{2}\left( {10 - 4} \right) = 3\,\,cm\)
Do $ABCD$ là hình thang cân nên $AD = BC = 5cm$
Áp dụng định lý Py– ta – go vào tam giác $ADH$ vuông tại $H$ ta có $A{D^2} = A{H^2} + D{H^2}$
$ \Rightarrow A{H^2} = A{D^2} - D{H^2} = {5^2} - {3^2} \Rightarrow AH = 4$
Vậy $AH = 4cm$ .
Cho tam giác $ABC$ cân tại $A$ . Trên các cạnh bên $AB$ , $AC$ lấy các điểm $M$ ,$N$ sao cho $BM$$ = CN$ .
Tứ giác $BMNC$ là hình gì?
-
A
Hình thang
-
B
Hình thang cân
-
C
Hình thang vuông
-
D
Cả A, B, C đều sai
Đáp án của giáo viên lời giải hay : B
Bước 1: Chứng minh \(MN{\rm{//}}BC\)
Bước 2: Hình thang \(MNCB\) có hai góc ở đáy bằng nhau nên nó là hình thang cân.
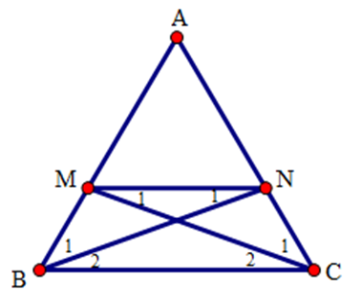
Ta có:$AB = AM + MB$ và $AC = AN + NC$ . Mà $AB = AC$ (do tam giác $ABC$ cân tại$A$ )và $BM = NC$ ( gt)
Suy ra $AN = AM$
Xét tam giác $AMN$ có: $AM = AN$ (cmt)
Suy ra tam giác $AMN$ cân tại$A$ . Suy ra \(\widehat {AMN} = \widehat {ANM}\)
Xét tam giác $ANM$ có: \(\widehat A + \widehat {AMN} + \widehat {ANM} = {180^0}\)(tổng ba góc trong một tam giác)
\(\widehat {AMN} = \dfrac{{{{180}^0} - \widehat A}}{2}\)( vì \(\widehat {AMN} = \widehat {ANM}\) ) (1)
Xét tam giác $ABC$ cân tại $A$ ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong một tam giác) nên $\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2}$ ( vì \(\widehat B = \widehat C\) ) (2)
Từ (1) và (2) \(\widehat {AMN} = \widehat B\)
Mà $\widehat {AMN},\widehat B$là hai góc đồng vị nên $MN$ //$BC$ .
Xét tứ giác $MNCB$ có $MN$ // $BC$ nên $MNCB$ là hình thang.
Lại có \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại$A$ ) nên $MNCB$ là hình thang cân.
Các điểm $M,N$ thỏa mãn điều kiện gì để $BM = MN = NC$ ?
-
A
$M \in AB$ sao cho \(BM = \dfrac{1}{3}AB\) , $N \in AC$ sao cho \(CM = \dfrac{1}{3}AC\)
-
B
Các điểm $M,N$ lần lượt là trung điểm \(AB,\,AC\) .
-
C
Các điểm $M,N$ lần lượt là chân các đường cao kẻ từ $B,C$ đến \(AC,\,AB\) .
-
D
Các điểm $M,N$ lần lượt là chân các đường phân giác góc \(ABC\) và góc \(BCA\) của tam giác \(ABC\) .
Đáp án của giáo viên lời giải hay : D
Ta sử dụng tính chất tam giác cân để suy ra điều kiện của \(M,\,N\) .
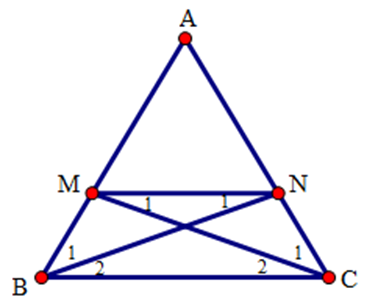
Ta có $BM = MN$ khi và chỉ khi \(\Delta MNB\) cân tại \(M \Rightarrow \) \(\widehat {{N_1}} = \widehat {{B_1}}\)\( \Leftrightarrow \widehat {{B_1}} = \widehat {{B_2}}\)(vì \(\widehat {{N_1}} = \widehat {{B_2}}\)) nên \(BN\) là phân giác góc $ABC$.
Tương tự $MN = NC$ khi và chỉ khi \(\Delta MNC\) cân tại \(N \Rightarrow \)\(\widehat {{C_1}} = \widehat {{C_2}}\) nên \(CM\) là phân giác góc \(ACB\) .
Như vậy, nếu $BN$ và $CM$ là các đường phân giác của tam giác $ABC$ thì $BM = MN = CN.$
Cho hình thang cân $ABCD$ ($AB$ //$CD$ ) có hai đường chéo cắt nhau tại $I$ , hai đường thẳng \(AD\) và \(BC\) cắt nhau ở $K.$ Chọn khẳng định đúng.
-
A
$KI$ là đường trung trực của hai đáy \(AB\) và \(CD\) .
-
B
$KI$ là đường trung trực của đáy \(AB\) nhưng không là đường trung trực của $CD$
-
C
$KI$ là đường trung trực của đáy \(CD\) nhưng không là trung trực của \(AB\) .
-
D
$KI$ không là đường trung trực của cả hai đáy \(AB\) và \(CD\) .
Đáp án của giáo viên lời giải hay : A
Ta sử dụng tính chất của hình thang cân để chứng minh các điều kiện của đường trung trực
Ta sử dụng tính chất: Các điểm cách đều hai đầu mút của một đoạn thẳng đều nằm trên đường trung trực của đoạn thẳng ấy.
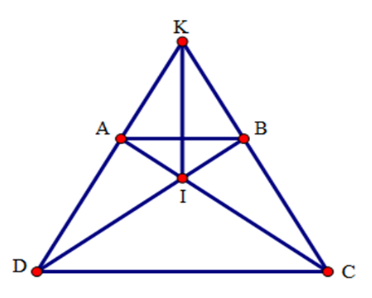
* Xét tam giác $ACD$ và tam giác $BDC$ có:
+$AD = BC$ (do $ABCD$ là hình thang cân)
+ $AC = BD$ (do $ABCD$ là hình thang cân)
+ $CD$ là cạnh chung
Suy ra \(\Delta ACD = \Delta BDC\)(c.c.c). Suy ra \(\widehat {ACD} = \widehat {BDC}\) (hai góc tương ứng).
Xét tam giác $ICD$ có \(\widehat {ACD} = \widehat {BDC}\)(cmt), suy ra tam giác $ICD$ cân tại$I$ .Dođó $ID = IC\,\,\,\left( 1 \right)$
Tam giác $KCD$ có hai góc ở đáy bằng nhau nên tam giác $KCD$ cân ở$K$ . Do đó $KC = KD$$\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $KI$ là đường trung trực của$CD$ (*)
* Xét tam giác $ADB$ và tam giác $BCA$ có:
+ $AD = BC$ (cmt)
+ $AB$ là cạnh chung
+ $AC = BD$
Suy ra \(\Delta ADB = \Delta BCA\) (c.c.c). Suy ra \(\widehat {ABD} = \widehat {BAC}\) .
Xét tam giác $IAB$ có \(\widehat {ABD} = \widehat {BAC}\) nên tam giác $IAB$ cân tại$I$ . Do đó $IA = IB$$\left( 3 \right)$
Ta có:$KA = KD-AD$ ;$KB = KC-BC$ . Mà$KD = KC$ , $AD = BC$ , do đó $KA = KB$$\left( 4 \right)$
Từ $\left( 3 \right)$ và $\left( 4 \right)$ suy ra $KI$ là đường trung trực của$AB$ . (**)
Từ (*) và (**) suy ra $KI$ là đường trung trực của hai đáy (đpcm)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Trên \(BC\) lấy điểm \(M\) sao cho \(CM = CA\). Đường thẳng đi qua \(M\) và song song với \(CA\) cắt \(AB\) tại \(I\).
Chọn câu đúng nhất. Tứ giác \(ACMI\) là hình gì ?
-
A
Hình thang cân
-
B
Hình thang vuông
-
C
Hình thang
-
D
Đáp án khác
Đáp án của giáo viên lời giải hay : B
+ Sử dụng: Tứ giác có hai cạnh đối song song là hình thang.
+ Sử dụng: Hình thang có 1 góc vuông là hình thang vuông.
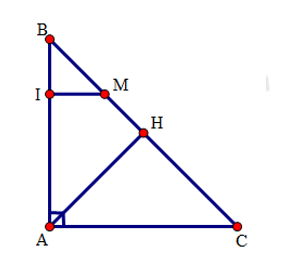
Tứ giác \(ACMI\) có: \(MI//AC\left( {gt} \right)\) và \(\hat A = 90^\circ (gt)\) nên là hình thang vuông.
Chọn câu đúng.
-
A
\(AB + AC > AH + BC\)
-
B
\(AB + AC < AH + BC\)
-
C
\(AB + AC = AH + BC\)
-
D
Chưa đủ điều kiện để so sánh
Đáp án của giáo viên lời giải hay : B
Sử dụng:
Tính chất hai tam giác bằng nhau.
Quan hệ giữa đường vuông góc và đường xiên.
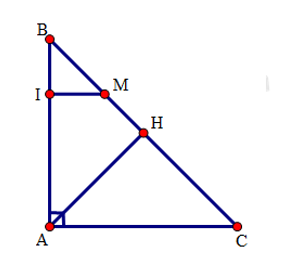
Xét tam giác \(AMC\) có: \(CM = AC(gt)\) nên tam giác \(AMC\) cân tại \(C\).
Suy ra \(\widehat {MAC} = \widehat {AMC\,}\,\,(1)\)
Xét tam giác AMH có: \(\widehat {MAH} = 90^\circ \widehat {- AMH}\) (hai góc phụ nhau) (2)
Xét tam giác ABC vuông tại A: \(\widehat {MAB} = \widehat {BAC} - \widehat {MAC} = 90^\circ - \widehat {MAC}\) (phụ nhau) (3)
Từ (1),(2) và (3) suy ra: \(\widehat {MAH} = \widehat {MAB} \Rightarrow \widehat {MAH} = \widehat {MAI}\)
Xét hai tam giác vuông \(\Delta AHM\) và \(\Delta AIM\) có:
AM (cạnh chung)
\(\widehat {MAH} = \widehat {MAI}\) (cmt)
\( \Rightarrow \;\Delta AHM = \Delta AIM\) (cạnh huyền-góc nhọn)
\( \Rightarrow AH = AI\) (hai cạnh tương ứng)
Lại có: \(MI\parallel AC (gt),AC \bot AB (gt) \Rightarrow MI \bot AB\).
Do đó \(BI < BM\,\,(4)\) (quan hệ giữa đường vuông góc và đường xiên)
Mặt khác:
\(AC = CM (gt) \,(5)\)
\(AI = AH (cmt) \,(6)\)
Cộng (6),(4),(5) vế theo vế ta được:
\(AI + BI + AC < AH + BM + CM\)
\( \Rightarrow AB + AC < AH + BC\).
Cho hình thang cân \(ABCD\left( {AB//CD} \right)\). Giả sử \(AB \le CD,\) chọn câu đúng.
-
A
\(B{D^2} - B{C^2} = CD.AB\)
-
B
\(B{D^2} - B{C^2} = A{B^2}\)
-
C
\(B{D^2} - B{C^2} = 2CD.AB\)
-
D
\(B{D^2} - B{C^2} = BC.AB\)
Đáp án của giáo viên lời giải hay : A
Sử dụng định lý Pytago trong tam giác vuông và hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\).
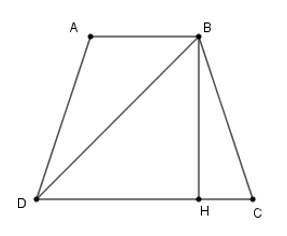
Kẻ \(BH \bot CD\) tại \(H.\)
Xét tam giác vuông \(BDH\), theo định lý Pytago, ta có \(B{D^2} = D{H^2} + B{H^2}\).
Xét tam giác vuông \(CBH\), theo định lý Pytago, ta có \(B{C^2} = C{H^2} + B{H^2}\).
Suy ra \(B{D^2} - B{C^2} = \left( {D{H^2} + B{H^2}} \right) - \left( {C{H^2} + B{H^2}} \right)\).
\( = D{H^2} - C{H^2} = \left( {DH + HC} \right)\left( {DH - HC} \right)\)\( = CD.AB\).
