Hãy chọn câu đúng. Trục đối xứng của hình thang cân là:
-
A
Đường thẳng đi qua trung điểm hai cạnh bên của hình thang cân.
-
B
Đường chéo của hình thang cân.
-
C
Đường thẳng vuông góc với hai đáy của hình thang cân.
-
D
Đường thẳng đi qua trung điểm hai đáy của hình thang cân.
Đáp án của giáo viên lời giải hay : D
Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Hãy chọn câu đúng?
-
A
Tam giác đều có ba trục đối xứng.
-
B
Tam giác cân có hai trục đối xứng.
-
C
Hình tam giác có ba trục đối xứng.
-
D
Hình thang cân có hai trục đối xứng.
Đáp án của giáo viên lời giải hay : A
+ Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm hai đáy nên hình thang cân có một trục đối xứng. Do đó A sai.
+ Tam giác cân có một trục đối xứng là đường trung trực hạ từ đỉnh cân nên B sai.
+ Tam giác thường thì không có trục đối xứng nên C sai.
+ Tam giác đều có ba trục đối xứng là ba đường trung trực của tam giác nên D đúng.
Cho tam giác $ABC$ cân tại $B$ , các đường trung tuyến $AA',BB',CC'$ . Trục đối xứng của tam giác $ABC$ là:
-
A
$AA'$
-
B
$BB'$
-
C
$AA'$ và $CC'$
-
D
$CC'$
Đáp án của giáo viên lời giải hay : B
Áp dụng định nghĩa hai điểm đối xứng nhau qua trục: hai điểm $A,A'$ được gọi là đối xứng nhau qua $d$ nếu $d$ là đường trung trực của $AA'$ .
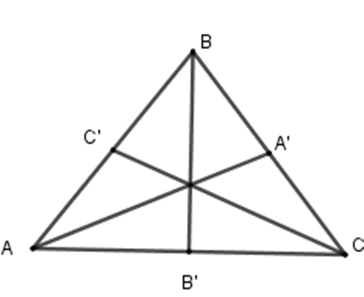
Do tam giác $ABC$ cân tại $B$ , nên đường trung tuyến $BB'$ đồng thời là đường trung trực.
Do đó $BB'$ là trục đối xứng của tam giác $ABC$.
Hãy chọn câu sai:
-
A
Nếu hai góc đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
-
B
Nếu hai tam giác đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
-
C
Nếu hai tam giác đối xứng với nhau qua một đường thẳng thì chu vi của chúng bằng nhau.
-
D
Nếu hai tia đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Đáp án của giáo viên lời giải hay : D
Ta sử dụng chú ý: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Vì hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau nên D sai.
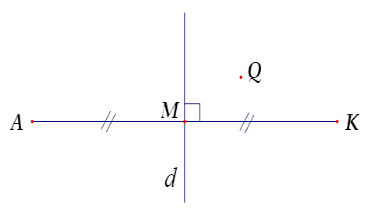
Cho hình vẽ. Hãy chọn câu đúng.
-
A
Điểm đối xứng với \(A\) qua đường thẳng \(d\) là \(A\).
-
B
Điểm đối xứng với \(K\) qua đường thẳng \(d\) là \(K\).
-
C
Điểm đối xứng với \(A\) qua đường thẳng \(d\) là \(K\).
-
D
Điểm đối xứng với \(Q\) qua đường thẳng \(d\) là \(Q\).
Đáp án của giáo viên lời giải hay : C
Ta sử dụng định nghĩa: Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó.
Từ hình vẽ ta có đường thẳng \(d\) là đường trung trực của đoạn thẳng \(AK\) nên Điểm đối xứng với \(A\) qua đường thẳng \(d\) là \(K\).
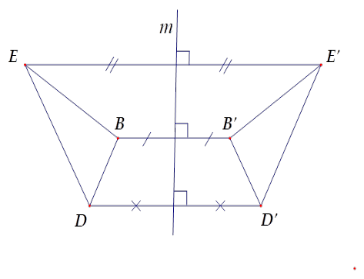
Hãy chọn câu sai.
-
A
Hai đoạn thẳng \(EB\) và \(E'B'\) đối xứng nhau qua \(m\).
-
B
Hai đoạn thẳng \(DB\) và \(D'B'\) đối xứng nhau qua \(m\).
-
C
Hai tam giác \(DEB\) và \(D'E'B'\) đối xứng nhau qua \(m\).
-
D
Hai đoạn thẳng \(DE\) và \(D'B'\) đối xứng nhau qua \(m\).
Đáp án của giáo viên lời giải hay : D
Bước 1: Ta sử dụng định nghĩa: “ Hai điểm $A,B$ gọi là đối xứng với nhau qua đường thẳng $d$ nếu $d$ là đường trung trực của đoạn thẳng nối hai điểm đó ” để tìm các cặp điểm đối xứng nhau qua đường thẳng \(m\) .
Bước 2: Từ đó suy ra các đoạn thẳng và tam giác đối xứng nhau qua đường thẳng \(m\) .
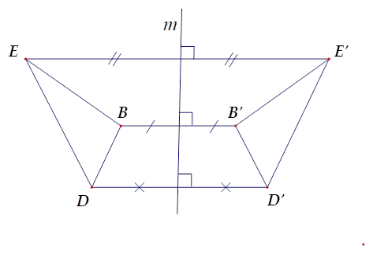
Từ hình vẽ ta có \(A\) và \(A'\) đối xứng nhau qua đường thẳng \(m\); \(B\) và \(B'\) đối xứng nhau qua đường thẳng \(m\); \(C\) và \(C'\) đối xứng nhau qua đường thẳng \(m\).
Suy ra hai đoạn thẳng \(EB\) và \(E'B'\) đối xứng nhau qua \(m\).
Hai đoạn thẳng \(DB\) và \(D'B'\) đối xứng nhau qua \(m\).
Hai tam giác \(DEB\) và \(D'E'B'\) đối xứng nhau qua \(m\).
Hai đoạn thẳng \(DE\) và \(D'E'\) đối xứng nhau qua \(m\) nên D sai.
Cho đoạn thẳng $AB$ có độ dài $3cm$và đường thẳng $d$ . Đoạn thẳng $A'B'$ đối xứng với $AB$ qua $d$ . Độ dài đoạn thẳng $A'B'$ là:
-
A
$3cm$
-
B
$6cm$
-
C
$9cm$
-
D
$12cm$
Đáp án của giáo viên lời giải hay : A
Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.” Từ đó suy ra độ dài đoạn $A'B'$.
Vì đoạn thẳng $A'B'$ đối xứng với $AB$ qua $d$ nên \(A'B' = AB = 3\,cm\) .
Cho tam giác $ABC$ và tam giác $A'B'C'$ đối xứng nhau qua đường thẳng $d$ biết $AB = 4cm,BC = 7cm$ và chu vi của tam giác $ABC = 17cm$. Khi đó độ dài cạnh $C'A'$ của tam giác $A'B'C'$ là:
-
A
$17cm$
-
B
$6cm$
-
C
$7cm$
-
D
$4cm$
Đáp án của giáo viên lời giải hay : B
Bước 1: Tính độ dài cạnh \(AC\) dựa vào chu vi tam giác \(ABC\) .
Bước 2: Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.” Từ đó suy ra độ dài đoạn $A'C'$.
+ Xét tam giác \(ABC\) có chu vi \({P_{ABC}} = AB + AC + BC \Rightarrow AC = {P_{ABC}} - AB - BC = 17 - 4 - 7\) \( = 6\,cm\) .
+ Vì tam giác $ABC$ và tam giác $A'B'C'$ đối xứng nhau qua đường thẳng $d$ nên \(AC = A'C' = 6\,cm\) .
Cho tam giác \(ABC\), trong đó \(AB = 11\,cm,AC = 15\,cm\). Vẽ hình đối xứng với tam giác \(ABC\) qua trục là cạnh \(BC\). Chu vi của tứ giác tạo thành là:
-
A
\(52\,cm\).
-
B
\(54\,cm\).
-
C
\(26\,cm\).
-
D
\(51\,cm\).
Đáp án của giáo viên lời giải hay : A
Bước 1: Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.”
Bước 2: Từ đó suy ra độ dài các cạnh còn lại rồi tính chu vi tứ giác.
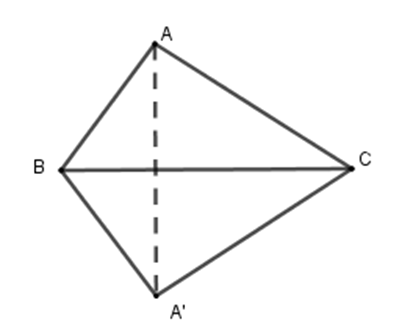
Gọi \(A'\) là điểm đối xứng với \(A\) qua \(BC\) . Khi đó tam giác \(A'BC\) đối xứng với tam giác \(ABC\) qua \(BC\) .
Tứ giác tạo thành là \(ABCA'\) .
Ta có \(A'B = AB = 11\,cm\) (vì \(A'B\) và \(AB\) đối xứng nhau qua \(BC\) )
\(A'C = AC = 15\,cm\) ( vì \(A'C\) và \(AC\) đối xứng nhau qua \(BC\) )
Chu vi tứ giác \(ABCA'\) là \(P = AB + AC + A'B + A'C = 11 + 15 + 11 + 15 = 52\,cm\) .
Cho hình vuông $ABCD$ cạnh bằng $a$. $M$ và $N$ là hai điểm lưu động lần lượt trên cạnh $AB$ và $AD$ sao cho \(\widehat {MCN} = {45^0}\). Vẽ tia $Cx$ vuông góc với $CN,Cx$ cắt đường thẳng $AB$ tại $E$.
Chọn kết luận đúng nhất.
-
A
$E$ là điểm đối xứng của $N$ qua $CM$.
-
B
Tam giác $CEN$ là tam giác cân tại .$C$.
-
C
Cả A, B đều đúng.
-
D
Cả A, B đều sai.
Đáp án của giáo viên lời giải hay : C
+ Ta chứng minh \(CE = CN\) suy ra tam giác \(CEN\) cân tại \(C\) .
+Ta chứng minh $CM$ là tia phân giác đồng thời là trung trực của $NE$ nên $E$ đối xứng với $N$ qua $CM$.
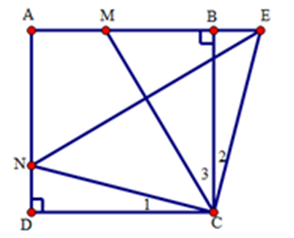
Ta có $CN \bot CE\,\left( {gt} \right)$ mà \(\widehat {MCN} = {45^0}\) nên \(\widehat {MCE} = {45^0}\) hay $\widehat {{C_2}} + \widehat {{C_3}} = {45^0}$. Mà $\widehat {{C_1}} + \widehat {{C_3}} = {45^0}$(vì \(\widehat {MCN} = {45^0}\)) nên $\widehat {{C_1}} = \widehat {{C_2}}$.
Xét tam giác $CDN$ và tam giác $CBE$ có:
$BC = DC$ (do $ABCD$ là hình vuông); \(\widehat D = \widehat B = {90^0}\) ; $\widehat {{C_1}} = \widehat {{C_2}}$(cmt)
Suy ra \(\Delta CDN = \Delta CBE(g.c.g)\) .Suy ra $CN = CE$
Xét tam giác $CEN$ có $CN = CE$ (cmt) nên tam giác $CEN$ là tam giác cân tại $C$.
Suy ra phân giác $CM$ đồng thời là đường trung trực của $NE$ .
Vậy E là điểm đối xứng của $N$ qua $CM$ .
Tính chu vi của tam giác \(AMN\) theo \(a\) .
-
A
\(4a\).
-
B
\(3a\).
-
C
\(a\).
-
D
\(2a\).
Đáp án của giáo viên lời giải hay : D
Bước 1: Ta sử dụng chú ý: “ Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.”
Bước 2: Từ đó ta biến đổi các cạnh của tam giác để xuất hiện các cạnh của hình vuông để tính chu vi tam giác \(AMN\) .
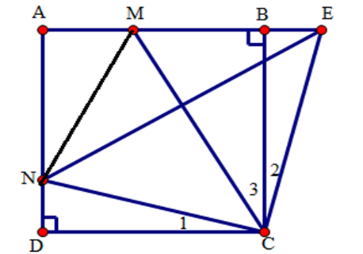
Ta có: \(\Delta CMN = \Delta CME\)(do tính đối xứng qua $CM$ )
Nên $MN = ME$
Suy ra chu vi tam giác \(AMN\) là:
$AM + AN + MN = AM + AN{\rm{ }} + ME = AM + AN + MB + BE$
$ = AM + AN + MB + ND$ (vì \(\Delta CDN = \Delta CBE\) (cmt) nên $BE = ND$)
$ = \left( {AM{\rm{ }} + MB} \right) + \left( {AN + ND} \right) = 2a$
Vậy chu vi tam giác $AMN$ bằng $2a$ .
Cho tam giác \(ABC\) có \(\widehat A = {20^0};\widehat B = {80^0}\), \(d\) là trung trực của cạnh \(AB\). Trên cạnh \(AC\), lấy điểm \(M\) sao cho \(AM = BC\) và gọi \(M'\) là điểm đối xứng của \(M\) qua \(d\).
Tam giác \(M'BC\) là tam giác gì? Chọn đáp án đúng nhất.
-
A
đều
-
B
cân tại \(B\)
-
C
cân tại \(C\)
-
D
vuông cân tại \(M'\)
Đáp án của giáo viên lời giải hay : A
Sử dụng tính chất đối xứng của điểm, đoạn thẳng qua đường thẳng.
Chứng minh tam giác cân có một góc bằng \(60^\circ \).
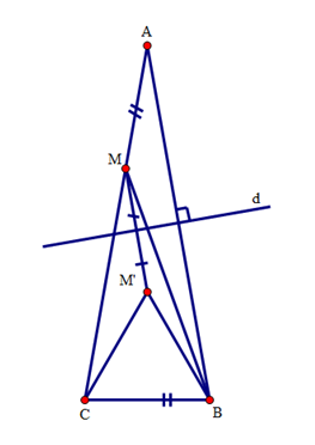
Do tính chất đối xứng qua \(d\), ta có \(AM = BM'\).
Mà \(AM = BC\left( {gt} \right)\) nên \(BM' = BC\).
Ta lại có: \(\widehat {M'BA} = \widehat {MAB} = {20^0}\) (do \(M,{\rm{ }}A\) đối xứng với \(M',{\rm{ }}B\) qua \(d\)).
Suy ra \(\widehat {M'BC} = \widehat B - {20^0} = {80^0} - {20^0} = {60^0}\).
Xét tam giác \(M'BC\) có \(BM' = BC\), \(\widehat {M'BC} = {60^0}\) do đó tam giác \(M'BC\) là tam giác đều.
Tính góc \(BMC\).
-
A
\(45^\circ \)
-
B
\(30^\circ \)
-
C
\(60^\circ \)
-
D
\(40^\circ \)
Đáp án của giáo viên lời giải hay : B
Ta thấy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB}\). Do đó để tính góc \(BMC\) ta lần lượt đi tính góc \(\widehat {CMM'}\) và \(\widehat {M'MB}\).
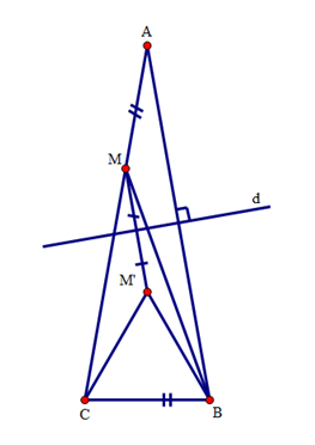
Ta cũng có: \(\widehat {MCB} = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{20}^0} + {{80}^0}} \right) = {80^0}\)
Suy ra \(\widehat {MCM'} = \widehat {MCB} - \widehat {M'CB} = {80^0} - {60^0} = {20^0}\)
Mà \(\widehat {CMM'} = \widehat A = {20^0}\)(góc đồng vị).
Nên \(\widehat {MCM'} = \widehat {CMM'} = {20^ \circ }\)
Suy ra \(M'C = M'M = M'B\).
Ta lại có: \(\widehat {M'MB} = \widehat {M'BM}\) (tam giác \(M'MB\) cân tại đỉnh \(M'\)); \(\widehat {M'MB} = \widehat {MBA}\)(so le trong).
Nên \(\widehat {M'BM} = \widehat {MBA} = \dfrac{1}{2}\widehat {M'BA} = {10^0}\)
Vậy \(\widehat {BMC} = \widehat {CMM'} + \widehat {M'MB} = {20^0} + {10^0} = {30^0}\)
Cho hai điểm $A,B$ nằm trên cùng một nửa mặt phẳng bờ là đường thẳng $d$ . Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. Tìm trên đường thẳng $d$ điểm $M$ sao cho tổng $MA + MB$ nhỏ nhất. Chọn khẳng định đúng nhất.
-
A
\(M\) là giao điểm của đoạn thẳng $AB$ và đường thẳng $d$.
-
B
\(M\) là giao điểm của đoạn thẳng $AB'$ và đường thẳng $d$.
-
C
Cả A, B đều đúng
-
D
Cả A, B đều sai.
Đáp án của giáo viên lời giải hay : B
Ta nhân thấy nếu $A,{\rm{ }}B$ nằm trên hai nửa mặt phẳng đối nhau bờ là đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất là đoạn $AB$ . Do vậy ta tìm cách đưa bài toán về trường hợp này.
Bằng cách dựng $B'$ đối xứng với $B$ qua $d$ ta đưa bài toán đã cho về trường hợp nêu trên vì $MB = MB'$ .
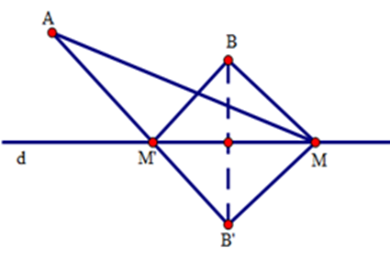
Gọi $B'$ là điểm đối xứng của $B$ qua đường thẳng $d$. $B'$ cố định.
Ta có $MB = MB'$ (tính chất đối xứng trục).
Xét ba điểm $M,{\rm{ }}A,{\rm{ }}B'$ ta có $MA + MB' \ge AB'$
Do đó $MA + MB \ge AB'$
Dấu “=” xảy ra khi và chỉ khi $A,M,B'$ thẳng hàng theo thứ tự đó hay $M$ là giao điểm của đoạn $AB'$ và đường thẳng $d$ .
Vậy khi \(M \equiv M'\) là giao điểm của đoạn thẳng $AB'$ và đường thẳng $d$ thì tổng $MA + MB$ nhỏ nhất, trong đó $B'$ là điểm đối xứng của $B$ qua $d$ .
Trên tia phân giác góc ngoài tại đỉnh \(C\) của tam giác \(ABC,\) lấy điểm \(M\) (\(M\) khác \(C\)). Chọn câu đúng.
-
A
\(MA + MB = AC + BC\)
-
B
\(MA + MB > AC + BC\)
-
C
\(MA + MB < AC + BC\)
-
D
Chưa đủ điều kiện để so sánh
Đáp án của giáo viên lời giải hay : B
+ Sử dụng tính chất đường trung trực của đoạn thẳng.
+ Sử dụng bất đẳng thức về ba cạnh của tam giác: Cho tam giác \(ABC\) thì \(\left| {AB - AC} \right| < BC < AB + AC\).
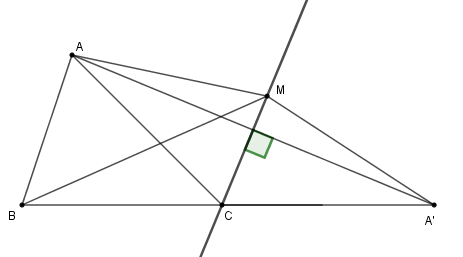
Trên tia đối của tia \(CB\) lấy điểm \(A'\) sao cho \(CA = CA'\)
Khi đó ta có: \(\Delta CAA'\) cân tại \(C\) có \(CM\) là phân giác \(\widehat {ACA'}\) nên \(CM\) cũng là đường trung trực của \(AA'\).
Từ đó ta có: \(MA = MA'\)
Nên \(MA + MB = MA' + MB\).
Xét tam giác \(MA'B\) có \(MA' + MB > A'B \Leftrightarrow MA + MB > A'C + BC\)
Hay \(MA + MB > AC + BC\) (vì \(CA = CA'\)).
