Phản ứng hạt nhân thực chất là:
-
A
Mọi quá trình dẫn đến sự biến đổi hạt nhân
-
B
Sự tương tác giữa các nuclon trong hạt nhân
-
C
Quá trình phát ra các tia phóng xạ của hạt nhân
-
D
Quá trình giảm dần độ phóng xạ của một lượng chất phóng xạ
Đáp án của giáo viên lời giải hay : A
Phản ứng hạt nhân là quá trình biến đổi của các hạt nhân
Phản ứng hạt nhân không tuân theo định luật bảo toàn:
-
A
Năng lượng
-
B
Động lượng
-
C
Khối lượng
-
D
Điện tích
Đáp án của giáo viên lời giải hay : C
Không có định luật bảo toàn khối lượng
\(\Delta {m_A} + \Delta {m_B} \ne \Delta {m_C} + \Delta {m_D}\) (vì \({{\rm{W}}_{l{k_A}}} + {{\rm{W}}_{l{k_B}}} \ne {{\rm{W}}_{l{k_C}}} + {{\rm{W}}_{l{k_D}}}\) )
Thông tin nào sau đây là sai khi nói về các định luật bảo toàn trong phản ứng hạt nhân?
-
A
Tổng số hạt nuclon của hạt tương tác bằng tổng số nuclon của các hạt sản phẩm
-
B
Tổng số các hạt proton của hạt tương tác bằng tổng các hạt proton của các hạt sản phẩm
-
C
Tổng năng lượng toàn phần của các hạt tương tác bằng tổng năng lượng toàn phần của các hạt sản phẩm
-
D
Tổng các vectơ động lượng của các hạt tương tác bằng tổng các vectơ động lượng của các hạt sản phẩm.
Đáp án của giáo viên lời giải hay : B
Xem lí thuyết phần 2
A, C, D - đúng
B - sai vì không có định luật bảo toàn số proton
Cho phương trình phản ứng: \(_{92}^{238}U + n \to _Z^AX + _{18}^{37}{\rm{Ar}}\). Trong đó Z, A là:
-
A
Z = 58, A = 143
-
B
Z = 74, A = 202
-
C
Z = 58, A = 139
-
D
Z = 44, A = 140
Đáp án của giáo viên lời giải hay : B
+ Vận dụng định luật bảo toàn số nuclon: \({A_A} + {\rm{ }}{A_B} = {\rm{ }}{A_C} + {\rm{ }}{A_D}\)
+ Vận dụng định luật bảo toàn điện tích: \({Z_A} + {\rm{ }}{Z_B} = {\rm{ }}{Z_C} + {\rm{ }}{Z_D}\)
+ Áp dụng định luật bảo toàn số nuclon, ta có: \(238 + 1 = A + 37 \to A = 202\)
+ Áp dụng định luật bảo toàn điện tích, ta có: \(92 + 0 = Z + 18 \to Z = 74\)
Cho phản ứng hạt nhân \(\alpha + {}_{13}^{27}Al \to _{15}^{30}P + X\) thì hạt X là
-
A
êlectron.
-
B
prôton
-
C
nơtron
-
D
pôzitron
Đáp án của giáo viên lời giải hay : C
PTPƯ: \(\alpha + {}_{13}^{27}Al \to {}_{15}^{30}P + {}_Z^AX\)
Áp dụng định luật bảo toàn điện tích và định luật bảo toàn số khối ta có:
2 + 13 = 15 + Z => Z = 0
4 + 27 = 30 + A => A = 1
Vậy X là nơtron
Cho phản ứng hạt nhân \({}_1^3T + {}_Z^AX \to {}_2^4He + {}_0^1n\), hạt nhân X là hạt nhân nào sau đây?
-
A
\({}_1^2D\)
-
B
\({}_1^1H\)
-
C
\({}_1^3T\)
-
D
\({}_2^4He\)
Đáp án của giáo viên lời giải hay : A
Áp dụng định luật bảo toàn điện tích và bảo toàn số khối ta xác định được : A = 2, Z = 1
=> X là \(_1^2D\)
Phản ứng nào sau đây thu năng lượng?
-
A
\(_1^1H + _1^2H \to _2^3He\)
-
B
\(_1^2H + _1^2H \to _2^4He\)
-
C
\(_1^2H + _1^3H \to _2^4He + _0^1n\)
-
D
\(_2^4He + _7^{14}N \to _8^{17}O + _1^1H\)
Đáp án của giáo viên lời giải hay : D
Cách 1:
D - là phản ứng thu năng lượng vì:
(mHe + mN) – (mO + mH) = (4,002603 + 14,003074)u – (16,999133 + 1,007825)u = -0,001281u < 0
Cách 2:
Ta thấy, các phản ứng A, B, C là phản ứng nhiệt hạch (là phản ứng kết hợp hai hạt nhân nhẹ thành một hạt nhân nặng hơn)
Lại có, các phản ứng nhiệt hạch tỏa năng lượng => Các phản ứng A, B, C tỏa năng lượng
Phản ứng D là phản ứng hạt nhân thông thường
=> Dùng phương pháp loại trừ ta suy ra phương án D - là phản ứng hạt nhân thu năng lượng
Chọn phát biểu SAI về phản ứng hạt nhân thu năng lượng
-
A
Tổng khối lượng của các hạt nhân sau phản ứng lớn hơn so với trước phản ứng
-
B
Tổng độ hụt khối của các hạt nhân sau phản ứng nhỏ hơn so với trước phản ứng
-
C
Các hạt nhân sau phản ứng bền vững hơn so với trước phản ứng
-
D
Không thể tự xảy ra và phải cung cấp năng lượng cho phản ứng
Đáp án của giáo viên lời giải hay : C
Trong phản ứng hạt nhân thu năng lượng:
- Tổng khối lượng của các hạt nhân sau phản ứng lớn hơn so với trước phản ứng
- Tổng độ hụt khối của các hạt nhân sau phản ứng nhỏ hơn so với trước phản ứng
- Các hạt nhân sau phản ứng kém bền vững hơn so với trước phản ứng
Phản ứng hạt nhân thu năng lượng không thể tự xảy ra và phải cung cấp năng lượng cho phản ứng.
Trong phản ứng thu năng lượng, các hạt nhân sau phản ứng kém bền vững hơn so với trước phản ứng
Cho phản ứng hạt nhân: \(_{\rm{1}}^{\rm{2}}{\rm{D}} + _{\rm{1}}^{\rm{3}}{\rm{T}} \to _{\rm{2}}^{\rm{4}}{\rm{He}} + _{\rm{0}}^{\rm{1}}{\rm{n}}\). Biết năng lượng liên kết riêng của các hạt nhân tương ứng là: εD = 1,11 MeV/nuclôn, εT = 2,83 MeV/nuclôn, εHe = 7,10 MeV/nuclôn. Năng lượng tỏa ra của phản ứng hạt nhân này là
-
A
17,69 MeV
-
B
18,26 MeV
-
C
17,25 MeV
-
D
16,52 MeV
Đáp án của giáo viên lời giải hay : A
Công thức tính năng lượng toả ra của phản ứng: ∆E = Wlks – Wlkt (Wlkt; Wlks lần lượt là tổng năng lượng liên kết của các hạt trước và sau phản ứng)
Công thức liên hệ giữa năng lượng liên kết và năng lượng liên kết riêng ε là: Wlk = A.ε
Năng lượng toả ra của phản ứng hạt nhân: \(\Delta {\rm{E}} = {{\rm{W}}_{lkHe}}{\rm{ - }}{{\rm{W}}_{lkD}}{\rm{ - }}{{\rm{W}}_{lkT}}{\rm{ = (4}}{{\rm{\varepsilon }}_{{\rm{He}}}} - {\rm{3}}{{\rm{\varepsilon }}_{\rm{T}}} - {\rm{2}}{{\rm{\varepsilon }}_{\rm{D}}}{\rm{)}} = {\rm{17,69MeV}}\)
Một prôtôn có động năng Kp = 1,5MeV bắn vào hạt nhân \({}_3^7Li\) đang đứng yên thì sinh ra 2 hạt X có bản chất giống nhau và không kèm theo bức xạ gamma. Tính động năng của mỗi hạt X? Cho mLi = 7,0144u; mp = 1,0073u; mX = 4,0015u; 1uc2 = 931MeV.
-
A
9,4549MeV
-
B
9,6 MeV
-
C
9,7 MeV
-
D
4,5 MeV
Đáp án của giáo viên lời giải hay : A
Năng lượng toả ra của phản ứng: ∆E = (mt – ms)c2 = Ks - Kt
(mt, Kt lần lượt là tổng khối lượng và tổng động năng của những hạt trước phản ứng; ms, Ks lần lượt là tổng khối lượng và tổng động năng của những hạt sau phản ứng)
Phương trình phản ứng: \(p + {}_3^7Li \to {}_2^4X + {}_2^4X\)
Ta có năng lượng toả ra của phản ứng:
∆E = (mLi + mP - 2mX)c² = (7,0144 + 1,0073 – 2.4,0015).931 = 17,4097 MeV
\(\Delta E = 2{K_\alpha } - {K_p} \to {K_\alpha } = \frac{{\Delta E + {K_p}}}{2} = 9,4549MeV\)
Trong phản ứng hạt nhân tỏa năng lượng của hai hạt nhân X1 và X2 tạo thành hạt nhân Y và một nơtron bay ra: \(_{{Z_1}}^{{A_1}}{X_1} + _{{Z_2}}^{{A_2}}{X_2} \to _Z^AY + n\) nếu năng lượng liên kết của các hạt nhân X1, X2 và Y lần lượt là a, b, c thì năng lượng được giải phóng trong phản ứng đó:
-
A
a + b + c
-
B
a + b – c
-
C
c - b – a
-
D
không tính được vì không biết động năng của các hạt trước phản ứng
Đáp án của giáo viên lời giải hay : C
Áp dụng công thức tính năng lượng toả ra của phản ứng hạt nhân ∆E = Wlks – Wlkt
Trong đó Wlkt, Wlks lần lượt là tổng năng lượng liên kết của các hạt trước và sau phản ứng
Năng lượng được giải phóng trong phản ứng là: \({W_{toa}} = {W_{lkY}}-{W_{lk{X_1}}}-{W_{lk{X_2}}} = c-b-a\)
Để phản ứng \({}_6^{12}C + \gamma \to 3{}_2^4He\) có thể xảy ra, lượng tử γ phải có năng lượng tối thiểu là bao nhiêu? Cho biết mC = 11,9967u; mα = 4,0015u; 1u.1c2 = 931MeV.
-
A
7,50 MeV
-
B
7,44 MeV
-
C
7,26 MeV
-
D
8,26 MeV
Đáp án của giáo viên lời giải hay : C
Để phản ứng xảy ra thì lượng tử γ phải có năng lượng tối thiểu bằng năng lượng thu vào của phản ứng.
Năng lượng thu vào của phản ứng hạt nhân: Wthu = (ms – mt)c2
Trong đó: mt, ms lần lượt là tổng khối lượng của các hạt trước và sau phản ứng.
Để phản ứng xảy ra thì lượng tử γ phải có năng lượng tối thiểu bằng năng lượng thu vào của phản ứng:
Wγ = Wthu = (3mα - mC ).c² = ( 3.4,0015 - 11,9967).931 = 7,26 MeV
Tổng hợp hạt nhân heli từ phản ứng hạt nhân \({}_1^1H + {}_3^7Li \to {}_2^4He + X\). Mỗi phản ứng trên tỏa năng lượng \(17,3 MeV\). Năng lượng tỏa ra khi tổng hợp được \(0,5 mol\) heli là
-
A
1,3.1024 MeV
-
B
2,6.1024 MeV
-
C
5,2.1024 MeV
-
D
2,4.1024 MeV
Đáp án của giáo viên lời giải hay : B
+ Áp dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng
+ Áp dụng công thức tính số nguyên tử chứa trong n (mol) chất: N = n.NA (NA = 6,02.1023)
Phương trình phản ứng: \({}_1^1H + {}_3^7Li \to {}_2^4He + {}_2^4He\)
\(0,5{\rm{ }}mol\) He có \(N{\rm{ }} = {\rm{ }}0,5.{N_A} = {\rm{ }}3,{01.10^{23}}\) nguyên tử
Vì mỗi phản ứng tỏa năng lượng \(17,3{\rm{ }}MeV\) tạo ra được 2 hạt Heli
\( \to \) Năng lượng tỏa ra khi tổng hợp được 0,5 mol heli là: \(17,3.\dfrac{N}{2} = 17,3.\dfrac{{3,{{01.10}^{23}}}}{2} = 2,{6.10^{24}}MeV\)
Xét phản ứng hạt nhân \({}_{13}^{27}Al + \alpha \to {}_{15}^{30}P + n\). Cho khối lượng của các hạt nhân mAl = 26,9740 u, mP = 29,9700 u, mα = 4,0015 u, mn = 1,0087 u, 1u = 931,5 MeV/c2. Phản ứng đó
-
A
tỏa năng lượng ≈ 2,98 MeV
-
B
thu năng lượng ≈ 2,98 MeV
-
C
tỏa năng lượng ≈ 29,8 MeV
-
D
thu năng lượng ≈ 29,8 MeV
Đáp án của giáo viên lời giải hay : B
Sử dụng lí thuyết về phản ứng hạt nhân và công thức tính năng lượng phản ứng hạt nhân
mt > ms => phản ứng toả năng lượng: Wtoả = (mt - ms)c2
mt < ms => phản ứng thu năng lượng: Wthu = (ms – mt)c2
Tổng khối lượng của các hạt trước phản ứng: \({m_t} = {m_{Al}} + {m_\alpha } = 30,9755u\)
Tổng khối lượng của các hạt sau phản ứng: \({m_s} = {m_P} + {m_n} = 30,9787u\)
Do mt < ms \( \to \) Phản ứng thu năng lượng
Năng lượng thu vào là: \({W_{thu}} = ({m_s} - {m_t}){c^2} = 3,{2.10^{ - 3}}.931,5 = 2,98(MeV)\)
Cho phản ứng hạt nhân \({}_1^3H + {}_1^2H \to {}_2^4He + {}_0^1n + 17,6MeV\) . Coi khối lượng nguyên tử Heli gần bằng số khối của nó. Năng lượng tỏa ra khi tổng hợp được 1 gam khí Heli là.
-
A
4,24.1011(J)
-
B
4,24.1013(J)
-
C
4,24.1012(J)
-
D
4,24.1010(J)
Đáp án của giáo viên lời giải hay : A
Sử dụng lí thuyết về năng lượng trong phản ứng hạt nhân.
Công thức tính số hạt chứa trong m(gam) chất: N = n. NA = m.NA/A (n là số mol; NA = 6,02.1023, A là số khối)
+ Theo phương trình phản ứng, năng lượng tỏa ra khi tổng hợp được 1 hạt nhân nguyên tử Heli là E = 17,6 MeV
+ Trong 1 g khí He có số hạt nhân nguyên tử là: \(N = n.{N_A} = \frac{m}{A}.{N_A} = \frac{1}{4}.6,{02.10^{23}} = 1,{505.10^{23}}\)
Để tổng hợp được 1 g khí He tỏa ra một năng lượng là:
\(E = N.\Delta E = 1,{505.10^{23}}.17,6 = 2,{649.10^{24}}(MeV) = 4,{238.10^{11}}(J)\)
Cho khối lượng của hạt nhân \({}_2^4He\); prôtôn và nơtron lần lượt là 4,0015 u; 1,0073 u và 1,0087 u.Lấy 1 u = 1,66.10–27 kg; c = 3.108 m/s; NA = 6,02.1023 mol–1. Năng lượng tỏa ra khi tạo thành 1 mol \({}_2^4He\) từ các nuclôn là
-
A
2,74.106 J
-
B
2,74.1012 J
-
C
1,71.106 J
-
D
1,71.1012 J.
Đáp án của giáo viên lời giải hay : B
+ Sử dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng
+ Áp dụng công thức tính năng lượng toả ra hay thu vào của phản ứng hạt nhân ∆E = (mt – ms)c2
+ Công thức tính số hạt chứa trong n (mol) chất: N = n.NA (NA = 6,02.1023 (số Avogadro))
Phương trình phản ứng: \(2{}_1^1p + 2{}_0^1n \to {}_2^4He\)
1MeV = 1,6.10-13J
Năng lượng toả ra khi tạo thành một hạt nhân He là: \(\Delta E{\rm{ = (2}}{{\rm{m}}_p} + 2{m_n} - {m_{He}}){c^2} = 28,41075MeV\)
Số hạt nhân nguyên tử He chứa trong 1 mol nguyên tử He là: N = 6,02.1023
\( \to \) Năng lượng tỏa ra khi tạo thành 1 mol heli là:
\({\rm{E }} = {\rm{ }}N.\Delta E{\rm{ }} = {6,02.10^{23}}.28,41075{.1,6.10^{ - 13}} = {2,74.10^{12}}J\)
Chu trình Cacbon của Bethe như sau:
\(\begin{array}{l}p + {}_6^{12}C \to {}_7^{13}N;{}_7^{13}N \to {}_6^{13}C + {e^ + } + v;p + {}_6^{13}C \to {}_7^{14}N\\p + {}_7^{14}N \to {}_8^{15}O;{}_8^{15}O \to {}_7^{15}N + {e^ - } + v;p + {}_7^{15}N \to {}_6^{12}C + {}_2^4He\end{array}\)
Năng lượng tỏa ra trong một chu trình cacbon của Bethe bằng bao nhiêu ? Biết khối lượng các nguyên tử proton, hêli và êlectrôn lần lượt là 1.007825u, 4,002603u, 0,000549u, 1u = 931 MeV/c²
-
A
49,4MeV
-
B
25,7MeV
-
C
12,4 MeV
-
D
Không tính được vì không cho khối lượng của các nguyên tử còn lại
Đáp án của giáo viên lời giải hay : B
Công thức tính năng lượng toả ra hay thu vào của phản ứng hạt nhân: ∆E = (mt – ms)c2
Ta có: Wtỏa = [(mp+ mC12 – mN13) + (mN13 – mC13 – me ) + (mp+ mC13 - mN14 ) + (mp + mN14 – mO15 ) + ( mO15 – mN15 – me ) + (mp + mN15 – mC12 – mHe)].c² = (4.mp - 2.me – mHe).c² = 25,7MeV
Năng lượng tỏa ra trong một chu trình cacbon của Bethe bằng 25,7 MeV
Cho phản ứng hạt nhân \({}_0^1n + {}_3^6Li \to {}_1^3H + \alpha \). Hạt nhân \({}_3^6Li\) đứng yên, nơtron có động năng Kn = 2 MeV. Hạt α và hạt nhân \({}_1^3H\) bay ra theo các hướng hợp với hướng tới của nơtron những góc tương ứng bằng θ = 150 và φ = 300. Lấy tỉ số giữa các khối lượng hạt nhân bằng tỉ số giữa các số khối của chúng. Giả sử phản ứng không kèm theo bức xạ γ. Phản ứng tỏa hay thu bao nhiêu năng lượng?
-
A
thu 1,52 MeV
-
B
tỏa 1,66 MeV
-
C
thu 1,66 MeV
-
D
tỏa 1,52 MeV
Đáp án của giáo viên lời giải hay : C
+ Áp dụng định luật bảo toàn động lượng và công thức liên hệ giữa động lượng và động năng
+ Áp dụng định lí hàm số sin trong tam giác.
+ Công thức liên hệ giữa động năng và động lượng: p2 = 2mK.
+ Công thức tính năng lượng toả ra hoặc thu vào của phản ứng:\(\Delta E{\rm{ }} = {\rm{ }}{K_s}-{\rm{ }}{K_t}\)
(Ks, Kt lần lượt là tổng động năng của các hạt sau và tổng động năng của các hạt trước phản ứng)
Áp dụng đinh luật bảo toàn động lượng ta có: \(\overrightarrow {{P_n}} + \overrightarrow {{P_{Li}}} = \overrightarrow {{P_H}} + \overrightarrow {{P_\alpha }} \)
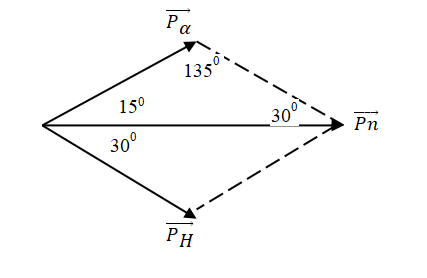
Ta có: P2 = 2mK, Kn = 2 MeV
Áp dụng định lí hàm số sin trong tam giác ta được: \(\frac{{{P_H}}}{{\sin 15}} = \frac{{{P_n}}}{{\sin 135}} = \frac{{{P_\alpha }}}{{\sin 30}}\)
\(\begin{array}{l} \Rightarrow {\left( {\frac{{{P_H}}}{{\sin 15}}} \right)^2} = {\left( {\frac{{{P_n}}}{{\sin 135}}} \right)^2} = {\left( {\frac{{{P_\alpha }}}{{\sin 30}}} \right)^2} \Leftrightarrow \frac{{3{K_H}}}{{{{\sin }^2}15}} = \frac{{1.{K_n}}}{{{{\sin }^2}135}} = \frac{{4{K_\alpha }}}{{{{\sin }^2}30}}\\ \Rightarrow {K_H} = 0,089MeV;{K_\alpha } = 0,25MeV\end{array}\)
∆E = Kα + KH – Kn = - 1,66 MeV < 0
=> Thu 1,66 MeV
Hạt α có động năng 4 MeV bắn vào một hạt nhân \({}_{4}^{9}Be\)đứng yên, gây ra phản ứng \(\alpha +{}_{4}^{9}Be\to {}_{6}^{12}C+n\).Biết phản ứng không kèm theo bức xạ γ. Hai hạt sinh ra có vectơ vận tốc hợp với nhau một góc bằng 70°. Biết khối lượng của hạt α, \({}_{4}^{9}Be\)và n lần lượt là mα = 4,0015u, mBe = 9,01219u, mn = 1,0087u; lấy u = 931,5 MeV/c2. Động năng của hạt nhân \({}_{6}^{12}C\) xấp xỉ là
-
A
0,1952 MeV.
-
B
0,3178 MeV.
-
C
0,2132 MeV.
-
D
0,3531 MeV.
Đáp án của giáo viên lời giải hay : B
Sử dụng công thức tính năng lượng toả ra của phản ứng hạt nhân
Áp dụng định luật bảo toàn động lượng và công thức liên hệ giữa động năng và động lượng: \({{p}^{2}}=2mK\)
+ Năng lượng toả ra của phản ứng là :
\(\Delta E=\left( {{m}_{\alpha }}+{{m}_{Be}}-{{m}_{C}}-{{m}_{n}} \right){{c}^{2}}={{K}_{C}}+{{K}_{n}}-{{K}_{\alpha }}=4,65(MeV)\to {{K}_{C}}+{{K}_{n}}=8,65(MeV)\)
Áp dụng định luật bảo toàn động lượng ta có:
\(\overrightarrow{{{p}_{\alpha }}}=\overrightarrow{{{p}_{C}}}+\overrightarrow{{{p}_{n}}}\Leftrightarrow {{p}_{\alpha }}^{2}=p_{C}^{2}+p_{n}^{2}+2.{{p}_{n}}.{{p}_{C}}.cos\text{7}{{\text{0}}^{o}}\)
\(\to 2{{m}_{\alpha }}{{K}_{\alpha }}=2{{m}_{C}}{{K}_{C}}+2{{m}_{n}}{{K}_{n}}+2.\sqrt{2.{{m}_{C}}{{K}_{C}}}.\sqrt{2.{{m}_{n}}{{K}_{n}}}.c\text{os7}{{\text{0}}^{o}}\to {{K}_{C}}=0,3178(MeV)\)
Cho phản ứng hạt nhân \({}_{17}^{37}Cl + p \to {}_{18}^{37}{\rm{Ar}} + {}_0^1n\) , khối lượng của các hạt nhân là mAr = 36,956889u, mCl = 36,956563 u; mn = 1,008670u , mp = 1,007276u; 1u = 931,5 MeV/c2. Năng lượng mà phản ứng này tỏa ra hoặc thu vào là
-
A
Tỏa ra 1,60218 MeV
-
B
Thu vào 1,60218 MeV
-
C
Tỏa ra 2,562112.10-19 J.
-
D
Thu vào 2,562112.10-19 J.
Đáp án của giáo viên lời giải hay : B
Áp dụng công thức năng lượng tỏa ra hay thu vào của phản ứng hạt nhân
W = (mtr - ms).c2.
Nếu W >0 thì phản ứng tỏa năng lượng; W < 0 thì phản ứng thu năng lượng
Áp dụng công thức năng lượng tỏa ra hay thu vào của phản ứng hạt nhân
W = (mtr - ms).c2 = (36,956563 + 1,007276- 36,956889-1,008670).931,5
= -1,60218 MeV
Vậy phản ứng thu năng lượng
