Cho chùm nơtron bắn phá đồng vị bền \(_{25}^{55}Mn\) ta thu được đồng vị phóng xạ \(_{25}^{56}Mn\). Đồng vị phóng xạ \(_{25}^{56}Mn\) có chu trì bán rã \(T{\rm{ }} = {\rm{ }}2,5h\) và phát xạ ra tia \({\beta ^ - }\). Sau quá trình bắn phá \(_{25}^{55}Mn\) bằng nơtron kết thúc người ta thấy trong mẫu trên tỉ số giữa số nguyên tử \(_{25}^{56}Mn\) và số nguyên tử \(_{25}^{55}Mn\) bằng \({10^{ - 10}}\) . Sau \(10\) giờ tiếp đó thì tỉ số giữa nguyên tử của hai loại hạt trên là:
-
A
\({3,125.10^{ - 12}}\)
-
B
\({6,25.10^{ - 12}}\)
-
C
\({2,5.10^{ - 11}}\)
-
D
\({1,25.10^{ - 11}}\)
Đáp án của giáo viên lời giải hay : B
Áp dụng định luật phóng xạ
Số nguyên tử còn lại sau phân rã: \(N = {N_0}{.2^{ - \dfrac{t}{T}}}\)
Số nguyên tử \(_{25}^{55}Mn\) sau khi ngừng quá trình bắn phá là không thay đổi, chỉ có số nguyên tử \(_{25}^{56}Mn\)phóng xạ thay đổi theo thời gian.
Ngay khi quá trình bắn phá kết thúc (t = 0), số nguyên tử \(_{25}^{55}Mn\) là N1, số nguyên tử \(_{25}^{56}Mn\) là N0, ta có: \({N_0} = \dfrac{{{N_1}}}{{{{10}^{10}}}}\)
Sau t = 10h = 4T, số nguyên tử \(_{25}^{56}Mn\) còn lại là:
\({N_2} = \dfrac{{{N_0}}}{{{2^4}}} = \dfrac{{{N_1}}}{{{{10}^{10}}{{.2}^4}}} = {\rm{}} > \dfrac{{{N_2}}}{{{N_1}}} = \dfrac{1}{{{{10}^{10}}{{.2}^4}}} = {6,25.10^{12}}\)
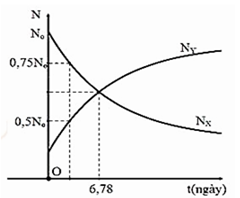
Hạt nhân X phóng xạ α để tạo thành hạt nhân Y bền theo phương trình . Người ta nghiên cứu một mẫu chất, sự phụ thuộc của số hạt nhân X(NX) và số hạt nhân Y( NY) trong mẫu chất đó theo thời gian đo được như trên đồ thị.Hạt nhân X có chu kỳ bán rã bằng
-
A
16 ngày
-
B
12 ngày
-
C
10 ngày
-
D
8 ngày
Đáp án của giáo viên lời giải hay : C
+ Số hạt nhân còn lại và bị phân rã : \(N = {N_0}{.2^{ - \dfrac{t}{T}}};\Delta N = {N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\)
+ Số hạt nhân mẹ bị phân rã bằng số hạt nhân con tạo thành
Tại thời điểm t = 0 ta có : \(\left\{ \begin{array}{l}{N_{X0}} = {N_0}\\{N_{Y0}} = 0,25{N_0}\end{array} \right.\)
Tại thời điểm t = 6,78s ta có : \(\left\{ \begin{array}{l}{N_X} = {N_0}{.2^{ - \dfrac{{6,78}}{T}}}\\{N_Y} = 0,25{N_0} + {N_0}.\left( {1 - {2^{ - \dfrac{{6,78}}{T}}}} \right)\end{array} \right.\)
Mà tại t = 6,78s có :
\(\begin{array}{l}{N_X} = {N_Y} \Leftrightarrow {N_0}{.2^{ - \dfrac{{6,78}}{T}}} = 0,25{N_0} + {N_0}.\left( {1 - {2^{ - \dfrac{{6,78}}{T}}}} \right)\\ \Leftrightarrow {2.2^{ - \dfrac{{6,78}}{T}}} = \dfrac{5}{4} \Leftrightarrow {2^{ - \dfrac{{6,78}}{T}}} = \dfrac{5}{8}\\ \Rightarrow - \dfrac{{6,78}}{T} = {\log _2}\dfrac{5}{8} \Rightarrow T = 10\left( {ngày} \right)\end{array}\)
Cho phản ứng hạt nhân \(_0^1n + _3^6Li \to _1^3H + \alpha \). Hạt Li đứng yên, nơtron có động năng \(2MeV\). Hạt \(\alpha \) và hạt nhân H bay ra theo các hướng hợp với hướng tới của nơtron những góc tương ứng bằng \({15^0}\) và \({30^0}\). Bỏ qua búc xạ gamma. Lấy tỉ số khối lượng các hạt bằng tỉ số giữa các số khối của chúng. Phản ứng thu hay tỏa bao nhiêu năng lượng?
-
A
Thu 4,8MeV
-
B
Tỏa 4,8MeV
-
C
Thu 1,66MeV
-
D
Tỏa 1,66MeV
Đáp án của giáo viên lời giải hay : C
Sử dụng định luật bảo toàn động lượng và định lý sin trong tam giác
Phương trình phản ứng là: \(_0^1n + _3^6Li \to _1^3H + _2^4He\)
Áp dụng định luật bảo toàn động lượng, ta vẽ được giản đồ vecto động lượng của phản ứng là:
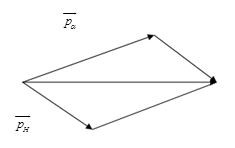
Áp dụng định lý hàm số sin trong tam giác ta có:
\(\begin{array}{l}\dfrac{{{p_n}}}{{\sin {{135}^0}}} = \dfrac{{{p_H}}}{{\sin {{15}^0}}} = \dfrac{{{p_\alpha }}}{{\sin {{30}^0}}}\\ = > \dfrac{{{p_H}}}{{{p_n}}} = \dfrac{{\sin {{15}^0}}}{{\sin {{135}^0}}} = > \dfrac{{{p_H}^2}}{{{p_n}^2}} = \dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > \dfrac{{{m_H}.{K_H}}}{{{m_n}.{K_n}}} = \dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > {K_H} = \dfrac{{1.2}}{3}.\dfrac{{{{\sin }^2}{{15}^0}}}{{{{\sin }^2}{{135}^0}}} = 0,089MeV\\\dfrac{{{p_{He}}}}{{{p_n}}} = \dfrac{{\sin {{30}^0}}}{{\sin {{135}^0}}} = > \dfrac{{{p_{He}}^2}}{{{p_n}^2}} = \dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > \dfrac{{{m_{He}}.{K_{He}}}}{{{m_n}.{K_n}}} = \dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}}\\ = > {K_{He}} = \dfrac{{1.2}}{4}.\dfrac{{{{\sin }^2}{{30}^0}}}{{{{\sin }^2}{{135}^0}}} = 0,25MeV\end{array}\)
Năng lượng thu vào \(\Delta E = {K_{tr}} - {K_s} = 2 - 0,089 - 0,25 = 1,66MeV\)
Tàu ngầm hạt nhân là một loại tàu ngầm vận hành nhờ sử dụng năng lượng của phản ứng hạt nhân. Nguyên liệu thường dùng là \({U^{235}}\). Mỗi phân hạch của hạt nhân \(\) tỏa ra năng lượng trung bình là \(200{\rm{ }}MeV\). Hiệu suất của lò phản ứng là \(25\% \). Nếu công suất của lò là 400MW thì khối lượng \({U^{235}}\) cần dùng trong một ngày xấp xỉ bằng:
-
A
\(1,75{\rm{ }}kg\)
-
B
\(2,59{\rm{ }}kg\)
-
C
\(1,69{\rm{ }}kg\)
-
D
\(2,67{\rm{ }}kg\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng công thức liên hệ giữa số hạt và khối lượng: \(N = \dfrac{m}{A}{N_A}\)
+ Hiệu suất: \(H = \dfrac{{{P_{ci}}}}{{{P_{tp}}}}\)
+ Năng lượng hạt nhân của lò phản ứng cung cấp cho tàu ngầm vận hành trong một ngày:
\(W{\rm{ }} = {\rm{ }}P.t{\rm{ }} = {\rm{ }}{400.10^6}.86400{\rm{ }} = {\rm{ }}{3,456.10^{13}}J\)
+ Do hiệu suất của lò đạt 25% nên năng lượng của mỗi phân hạch cung cấp là:
\(\Delta {\rm{W}} = 200.0,25 = 50MeV = {8.10^{ - 12}}J\)
+ Số phân hạch cần xảy ra để có năng lượng W là: \(N = \dfrac{{\rm{W}}}{{\Delta {\rm{W}}}} = {4,32.10^{24}}\)
+ Cứ một phân hạch cần 1 hạt \({U^{235}}\)
=> Số hạt\({U^{235}}\) dùng trong 1 ngày là: \(N{\rm{ }} = {\rm{ }}{4,32.10^{24}}\) hạt
+ Lại có: \(N = \dfrac{m}{A}.{N_A} \Rightarrow m = \dfrac{{N.A}}{{{N_A}}} = \dfrac{{{{4,23.10}^{24}}.235}}{{{{6,02.10}^{23}}}} \approx 1686,4g = 1,69kg\)
Tính chu kì bán rã \(T\) của một chất phóng xạ, cho biết tại thời điểm \({t_1}\), tỉ số giữa hạt con và hạt mẹ là \(7\), tại thời điểm \({t_2}\) sau \({t_1}\) \(414\) ngày thì tỉ số đó là \(63\)
-
A
126 ngày
-
B
138 ngày
-
C
207 ngày
-
D
552 ngày
Đáp án của giáo viên lời giải hay : B
+ Số hạt nhân con tạo thành bằng số hạt nhân mẹ bị phân rã
+ Số hạt nhân còn lại: \(N{\rm{ }} = {\rm{ }}{N_0}{.2^{ - \dfrac{t}{T}}} = {N_0}{e^{ - \lambda t}}\)
+ Số hạt nhân bị phân rã: \(\Delta N = {N_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right) = {N_0}\left( {1 - {e^{ - \lambda t}}} \right)\)
+ Tại thời điểm \({t_1}\) ta có: \(\dfrac{{\Delta N}}{N} = \dfrac{{(1 - {e^{ - \lambda {t_1}}})}}{{{e^{ - \lambda {t_1}}}}} = 7 \Rightarrow {e^{ - \lambda {t_1}}} = \dfrac{1}{8}{\rm{ }}\left( 1 \right)\)
+ Tại thời điểm ta có:
\(\begin{array}{l}\dfrac{{\Delta N}}{N} = \dfrac{{(1 - {e^{ - \lambda {t_2}}})}}{{{e^{ - \lambda {t_2}}}}} = 63\\ \Rightarrow \dfrac{{(1 - {e^{ - \lambda ({t_1} + 414)}})}}{{{e^{ - \lambda ({t_1} + 414)}}}} = 63\\ \Rightarrow \dfrac{{(1 - {e^{ - \lambda {t_1}}}.{e^{ - 414\lambda }})}}{{{e^{ - \lambda {t_1}}}.{e^{ - 414\lambda }}}} = 63{\rm{ }}\left( 2 \right)\end{array}\)
Thay (1) vào (2) ta được:
\(\begin{array}{l}\dfrac{{1 - 0,125{e^{ - 414\lambda }}}}{{0,125{e^{ - 414\lambda }}}} = 63\\ \to {e^{ - 414\lambda }} = 0,125 \to \lambda = \dfrac{{ - \ln 0,125}}{{414}}\end{array}\)
\( \to T = \dfrac{{414\ln 2}}{{ - \ln 0,125}} = 138\) ngày
Dùng một proton có động năng \(5,45{\rm{ }}MeV\) bắn vào hạt nhân \(_4^9Be\) đang đứng yên. Phản ứng tạo ra hạt nhân \(X\) và hạt \(\alpha \). Hạt \(\alpha \) bay ra theo phương vuông góc với phương tới của hạt proton và có động năng \(4,0{\rm{ }}MeV\). Khi tính động năng của các hạt, lấy khối lượng các hạt nhân tính theo đơn vị khối lượng nguyên tử bằng số khối của chúng. Năng lượng tỏa ra trong phản ứng này bằng:
-
A
\(1,145{\rm{ }}MeV\)
-
B
\(2,125{\rm{ }}MeV\)
-
C
\(4,225{\rm{ }}MeV\)
-
D
\(3,125{\rm{ }}MeV\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng định luật bảo toàn số khối và bảo toàn điện tích để viết phương trình phản ứng.
+ Sử dụng định luật bảo toàn động lượng trong phản ứng hạt nhân.
+ Công thức liên hệ giữa động lượng và động năng: \({p^2} = {\rm{ }}2mK\)
+ Công thức tính năng lượng toả ra của phản ứng: \(\Delta E{\rm{ }} = {\rm{ }}\left( {{m_t}-{\rm{ }}{m_s}} \right){c^2} = {\rm{ }}{K_s} - {\rm{ }}{K_t}\)
(Kt, Ks lần lượt là tổng động năng của các hạt trước và sau phản ứng)
+ PT phản ứng: \(p + _4^9Be \to \alpha {\rm{ }} + _3^6X\)
+ Theo định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}} {\rm{ }} = \overrightarrow {{p_\alpha }} {\rm{ }} + \overrightarrow {{p_X}} \)
=> ta biểu diễn bằng hình vẽ sau:
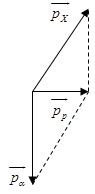
Từ hình vẽ ta có: \(p_X^2 = p_\alpha ^2 + p_p^2\)
Mà : \({p^2} = 2mK \Rightarrow {m_X}{K_X} = {m_\alpha }{K_\alpha } + {m_p}{K_p} \Rightarrow {K_X} = \dfrac{{{m_\alpha }{K_\alpha } + {m_p}{K_p}}}{{{m_X}}} = \dfrac{{4.4 + 1.5,45}}{6} = 3,575(MeV)\)
Năng lượng tỏa ra của phản ứng : \(\Delta E = {K_X} + {K_\alpha } - {K_p} = 3,575 + 4 - 5,45 = 2,125(MeV)\)
Pôlôni \(_{84}^{210}{\rm{Po}}\) là chất phóng xạ \(\alpha \) . Ban đầu có một mẫu nguyên chất. Khối lượng trong mẫu ở các thời điểm \(t{\rm{ }} = {\rm{ }}{t_0}\), \(t{\rm{ }} = {\rm{ }}{t_0} + {\rm{ }}2\Delta t\) và \(t{\rm{ }} = {\rm{ }}{t_0} + {\rm{ }}3\Delta t\) (\(\Delta t{\rm{ }} > {\rm{ }}0\)) có giá trị lần lượt là \({m_0}\) , \(8{\rm{ }}g\) và \(1{\rm{ }}g\). Giá trị của \({m_0}\) là:
-
A
\(64{\rm{ }}g\)
-
B
\(256{\rm{ }}g\)
-
C
\(512{\rm{ }}g\)
-
D
\(128{\rm{ }}g\)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính khối lượng chất còn lại: \(m = {m_0}{2^{ - \dfrac{t}{T}}}\)
Theo đề sau thời gian \(\Delta t\) khối lượng Pôlôni giảm từ \(8g\) xuống còn \(1{\rm{ }}g\):
\(\begin{array}{l}{m_3} = \dfrac{{{m_2}}}{8} = \dfrac{{{m_2}}}{{{2^3}}} = \dfrac{{{m_2}}}{{2\dfrac{{3T}}{T}}}\\ \to \Delta t = 3T\end{array}\)
Ta có:
\(\begin{array}{l}{m_2} = \dfrac{{{m_0}}}{{{2^{\dfrac{{2\Delta t}}{T}}}}} = \dfrac{{{m_0}}}{{{2^{\dfrac{{2.3T}}{T}}}}} = \dfrac{{{m_0}}}{{{2^6}}}\\ \to {m_0} = {m_2}{.2^6} = 8.64 = 512g\end{array}\)
Dùng hạt \(\alpha \) có động năng \(5,00 MeV\) bắn vào hạt nhân \(_7^{14}N\) đứng yên gây ra phản ứng: \(\alpha {\rm{}} + _7^{14}N \to _1^1H + X\) . Phản ứng này thu năng lượng \(1,21{\rm{ }}MeV\) và không kèm theo bức xạ gamma. Lấy khối lượng các hạt nhân tính theo đơn vị u bằng số khối của chúng. Khi hạt nhân X bay ra theo hướng lệch với hướng chuyển động của hạt α một góc lớn nhất thì động năng của hạt \(_1^1H\) có giá trị gần nhất với giá trị nào sau đây?
-
A
\(2,96{\rm{ }}MeV\)
-
B
\(2,58{\rm{ }}MeV\)
-
C
\(2,75{\rm{ }}MeV\)
-
D
\(2,43{\rm{ }}MeV\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng định luật bảo toàn số khối và bảo toàn điện tích để viết phương trình phản ứng.
+ Sử dụng định luật bảo toàn động lượng trong phản ứng hạt nhân.
+ Công thức liên hệ giữa động lượng và động năng: \({p^2} = {\rm{ }}2mK\)
+ Công thức tính năng lượng toả ra của phản ứng: \(\Delta E{\rm{ }} = {\rm{ }}\left( {{m_t}-{\rm{ }}{m_s}} \right){c^2} = {\rm{ }}{K_s} - {\rm{ }}{K_t}\)
(Kt, Ks lần lượt là tổng động năng của các hạt trước và sau phản ứng)
Ta có:
\(\begin{array}{l}{K_X} + {K_H} = 5 - 1,21 = 3,79\\ \to {K_H} = 3,79 - {K_X}\end{array}\)
Vẽ giản đồ véc tơ \(\overrightarrow {{P_\alpha }} {\rm{}} = \overrightarrow {{P_X}} {\rm{}} + \overrightarrow {{P_H}} \) ;
Gọi \(\beta \) là góc hợp bởi hướng lệch của hạt X so với hướng chuyển động của hạt \(\alpha \) ta có:
\(\begin{array}{l}cos\beta = \dfrac{{p_X^2 + p_\alpha ^2 - p_H^2}}{{2{p_X}{p_\alpha }}} = \dfrac{{17{K_X} + 20 - 3,79 + {K_X}}}{{4\sqrt {85} \sqrt {{K_X}} }}\\ = \dfrac{{18\sqrt {{K_X}} + \dfrac{{16,21}}{{\sqrt {{K_X}} }}}}{{4\sqrt {85} }}\end{array}\)
Ta có: \(18\sqrt {{K_X}} + \dfrac{{16,21}}{{\sqrt {{K_X}} }} \ge 2\sqrt {18\sqrt {{K_X}} .\dfrac{{16,21}}{{\sqrt {{K_X}} }}} \approx 34,16\)
=> Để \(\beta \) đạt giá trị lớn nhất khi: \(18\sqrt {{K_X}} = \dfrac{{16,21}}{{\sqrt {{K_X}} }} \to {K_X} = 0,9MeV\)
=> \({K_H} = 3,79 - {K_X} = 3,79 - 0,9 = 2,89MeV\)
Chất phóng xạ pôlôni \(_{84}^{210}Po\) phát ra tia \(\alpha\) và biến đổi thành chì \(_{82}^{206}Pb\) . Gọi chu kì bán rã của pôlôni là \(T\). Ban đầu \((t = 0)\) có một mẫu \(_{84}^{210}Po\) nguyên chất. Trong khoảng thời gian từ \(t = 0\) đến \(t = 2T\), có \(126 mg\) \(_{84}^{210}Po\) trong mẫu bị phân rã. Lấy khối lượng nguyên tử tính theo đơn vị u bằng số khối của hạt nhân của nguyên tử đó. Trong khoảng thời gian từ \(t = 2T\) đến \(t = 3T\), lượng chì được tạo thành trong mẫu có khối lượng là:
-
A
10,5 mg
-
B
20,6 mg
-
C
41,2 mg
-
D
61,8 mg
Đáp án của giáo viên lời giải hay : B
Vận dụng biểu thức tính khối lượng chất phân rã: \(\Delta m = {m_0}\left( {1 - {2^{ - \dfrac{t}{T}}}} \right)\)
Ta có
\({m_o} - \dfrac{{{m_o}}}{{{2^2}}} = 126mg \to {m_o} = 168mg\);
+ Thời điểm \(t = 2T\) ta có: \({m_0}' = \dfrac{{{m_0}}}{4} = 42mg\)
+ Số hạt Po bị phân rã trong thời gian từ \(2T\) đến \(3T\) là:
\(\begin{array}{l}\Delta N = \dfrac{{{m_o}'}}{{2.210}}.{N_A}\\ \to {m_{Pb}} = \dfrac{{\Delta N{A_{Pp}}}}{{{N_A}}} = \dfrac{{42}}{{2.210}}.206 = \dfrac{{103}}{5} = 20,6mg\end{array}\)
Cho phản ứng phân hạch của Urani 235: \(_{92}^{235}U + _0^1n \to _{42}^{95}Mo + _{57}^{139}La + 2_0^1n\). Biết khối lượng các hạt nhân: mU = 234,99u; mMo = 94,88u; mLa = 138,87u; mn = 1,0087u. Hỏi năng lượng tỏa ra khi 1 gam U phân hạch hết sẽ tương đương với năng lượng sinh ra khi đốt cháy bao nhiêu kg xăng? Biết rằng mỗi kg xăng cháy hết tỏa năng lượng 46.106 J.
-
A
20kg
-
B
1720kg
-
C
1820kg
-
D
1920kg
Đáp án của giáo viên lời giải hay : D
+ Công thức tính năng lượng toả ra của phản ứng: \(\Delta E{\rm{ }} = {\rm{ }}\left( {{m_t}-{\rm{ }}{m_s}} \right){c^2}\)
(mt, ms lần lượt là tổng khối lượng của các hạt trước và sau phản ứng)
+ Công thức liên hệ giữa số hạt và khối lượng: \(N = \dfrac{m}{A}{N_A}\)
Năng lượng toả ra khi 1 hạt U phân hạch là:
\(\begin{array}{l}\Delta E = \left( {\left( {{m_U} + {m_n}} \right) - \left( {{m_{Mo}} + {m_{La}} + 2{m_n}} \right)} \right){c^2}\\ = \left( {234,99 - 94,88 - 138,87 - 1,0087} \right)\;u{c^2}\\ = 0,2313.931,5 = 215,5MeV\end{array}\)
+ 1 (g) U235 chứa: \(N = \dfrac{m}{A}{N_A} = \dfrac{1}{{235}}{.6,02.10^{23}} = {2,56.10^{21}}\) hạt
=> 1 gam U phân hạch hết toả năng lượng: \(E = N.\Delta E = {5,52.10^{23}}MeV = {8,832.10^{10}}J\)
=> Lượng xăng cần sử dụng là: \(m = \dfrac{{{{8,832.10}^{10}}}}{{{{46.10}^6}}} = 1920kg\)
