Một sóng cơ dao động có bước sóng là $λ$. Khoảng cách giữa $n$ ngọn sóng liên tiếp là:
-
A
$n$ bước sóng
-
B
$n - 1$ bước sóng
-
C
$n + 1$ bước sóng
-
D
$2n$ bước sóng
Đáp án của giáo viên lời giải hay : B
Khoảng cách giữa $n$ ngọn sóng liên tiếp là: $n - 1$ bước sóng
Một người ngồi ở bờ biển quan sát thấy khoảng cách giữa năm ngọn sóng liên tiếp bằng $20 m$. Bước sóng là:
-
A
$5 m$
-
B
$4 m$
-
C
$16 m$
-
D
$40 m$
Đáp án của giáo viên lời giải hay : A
Khoảng cách giữa $n$ ngọn sóng liên tiếp là: $n - 1$ bước sóng
Ta có, khoảng cách giữa năm ngọn sóng liên tiếp là: $4λ = 20 m => λ = 5m$
Một người ngồi ở bờ biển đếm được $20$ ngọn sóng đi qua trước mặt trong $76s$. Chu kì dao động của nước biển là:
-
A
$2s$
-
B
$3,6s$
-
C
$3,8s$
-
D
$4s$
Đáp án của giáo viên lời giải hay : D
Thời gian truyền giữa n ngọn sóng liên tiếp là: $n - 1$ chu kì
Ta có, $20$ ngọn sóng đi qua trước mặt tương đương với $19$ bước sóng hay $19$ chu kì dao động
=> $19T = 76s => T = 4s$
Mối liên hệ giữa bước sóng $λ$, vận tốc truyền sóng $v$, chu kì $T$ và tần số $f$ của một sóng là:
-
A
\(f = \dfrac{1}{T} = \dfrac{v}{\lambda }\)
-
B
\(v = \dfrac{1}{f} = \dfrac{T}{\lambda }\)
-
C
\(\lambda = \dfrac{T}{v} = \dfrac{f}{v}\)
-
D
\(\lambda = \dfrac{T}{v} = vf\)
Đáp án của giáo viên lời giải hay : A
Vận dụng biểu thức: \(\lambda = \dfrac{v}{f} = vT\)
Ta có: \(\lambda = \dfrac{v}{f} = vT\)
Một sóng truyền trong một môi trường với vận tốc $110 m/s$ và có bước sóng $0,25 m$. Tần số của sóng đó là:
-
A
$50 Hz$
-
B
$220 Hz$
-
C
$440 Hz$
-
D
$27,5 Hz$
Đáp án của giáo viên lời giải hay : C
Vận dụng biểu thức: \(\lambda = \dfrac{v}{f} = vT\)
Ta có:
\(\lambda = \dfrac{v}{f} \to f = \dfrac{v}{\lambda } = \dfrac{{110}}{{0,25}} = 440Hz\)
Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số $120 Hz$, tạo ra sóng ổn định trên mặt chất lỏng. Xét $5$ gợn lồi liên tiếp trên một phương truyền sóng ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm $0,5m$. Tính tốc độ truyền sóng trên mặt chất lỏng:
-
A
$10 m/s$
-
B
$12 m/s$
-
C
$15 m/s$
-
D
$20 m/s$
Đáp án của giáo viên lời giải hay : C
+ Khoảng cách giữa n ngọn sóng liên tiếp là: n - 1 bước sóng
+ Vận dụng biểu thức: \(\lambda = \dfrac{v}{f} = vT\)
Ta có:
Khoảng cách giữa $5$ gợn lồi (ngọn sóng) là: $4λ = 0,5m => λ = 0,125 m$
\(\lambda = \dfrac{v}{f} \to v = \lambda f = 0,125.120 = 15m/s\)
Một sóng ngang truyền theo chiều dương trục $Ox$, có phương trình sóng là $u = 6cos(4πt-0,02πx)$; trong đó $u$ và $x$ tính bằng $cm$, $t$ tính bằng $s$. Sóng này có bước sóng là:
-
A
$150 cm$
-
B
$50 cm$
-
C
$100 cm$
-
D
$200 cm$
Đáp án của giáo viên lời giải hay : C
Áp dụng biểu thức: \(\Delta \varphi = \dfrac{{2\pi x}}{\lambda }\)
Ta có:
\(\Delta \varphi = \dfrac{{2\pi x}}{\lambda } = 0,02\pi x \to \lambda = 100cm\)
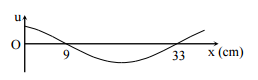
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm $t$, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục $Ox$. Bước sóng của sóng này bằng:
-
A
$48 cm$
-
B
$18 cm$
-
C
$36 cm$
-
D
$24 cm$
Đáp án của giáo viên lời giải hay : A
Đọc đồ thị li độ $u - x$
Từ đồ thị, ta có:
\(\dfrac{\lambda }{2} = 33 - 9 = 24cm \to \lambda = 48cm\)
Một nguồn phát sóng dao động theo phương trình \(u = ac{\rm{os20}}\pi {\rm{t}}\) (cm). Trong khoảng thời gian 2s sóng truyền đi được quãng đường bằng bao nhiêu lần bước sóng?
-
A
10
-
B
20
-
C
30
-
D
40
Đáp án của giáo viên lời giải hay : B
Vận dụng công thức tính chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\)
Ta có:
\(T = \dfrac{{2\pi }}{{20\pi }} = 0,1s\)
2s = 20T
=> Quãng đường sóng truyền đi trong 2s bằng 20 lần bước sóng
Một sóng cơ học có bước sóng $λ$ truyền theo một đường thẳng từ điểm $M$ đến điểm $N$. Biết khoảng cách $MN = d$. Độ lệch pha $\Delta \varphi $ của dao động tại hai điểm $M$ và $N$ là:
-
A
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
-
B
\(\Delta \varphi = \dfrac{{\pi d}}{\lambda }\)
-
C
\(\Delta \varphi = \dfrac{{\pi \lambda }}{d}\)
-
D
\(\Delta \varphi = \dfrac{{2\pi \lambda }}{d}\)
Đáp án của giáo viên lời giải hay : A
Độ lệch pha của hai dao động tại hai điểm M và N là: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Một nguồn dao động điều hoà với chu kỳ 0,04s. Vận tốc truyền sóng bằng 200cm/s. Hai điểm nằm trên cùng một phương truyền sóng và cách nhau 6 cm, thì có độ lệch pha:
-
A
$1.5\pi $
-
B
$1\pi $
-
C
$3,5\pi $
-
D
$2,5\pi $
Đáp án của giáo viên lời giải hay : A
+ Áp dụng biểu thức tính bước sóng: \(\lambda = vT\)
+ Áp dụng biểu thức tính độ lệch pha giữa 2 điểm: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Ta có:
Bước sóng:
\(\lambda = vT = 200.0,04 = 8cm\)
Độ lệch pha của hai dao động tại hai điểm là:
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi 6}}{8} = \dfrac{3}{2}\pi \)
Sóng cơ có tần số $50 Hz$ truyền trong môi trường với vận tốc $160 m/s$. Ở cùng một thời điểm, hai điểm gần nhau nhất trên một phương truyền sóng có dao động cùng pha với nhau, cách nhau
-
A
$3,2 m$
-
B
$2,4 m$
-
C
$1,6 m$
-
D
$0,8 m$
Đáp án của giáo viên lời giải hay : A
Áp dụng biểu thức tính bước sóng: \(\lambda = vT\)
Ta có bước sóng:
\(\lambda = \dfrac{v}{f} = \dfrac{{160}}{{50}} = 3,2m\)
Khoảng cách giữa hai điểm gần nhau nhất trên một phương truyền sóng dao động cùng pha với nhau là 1 bước sóng.
Một sóng ngang truyền trên sợi dây đàn hồi rất dài với tần số $500Hz$. Người ta thấy hai điểm $A, B$ trên sợi dây cách nhau $200cm$ dao động cùng pha và trên đoạn dây $AB$ có hai điểm khác dao động ngược pha với $A$. Tốc độ truyền sóng trên dây là:
-
A
$500cm/s$
-
B
$1000m/s$
-
C
$500m/s$
-
D
$250cm/s$
Đáp án của giáo viên lời giải hay : C
Áp dụng biểu thức tính tốc độ truyền sóng: \(v = \lambda f\)
2 điểm A, B dao động cùng pha và trên AB có 2 điểm khác dao động ngược pha với A.
\( \to AB = 2\lambda = 200cm \to \lambda = 100cm\)
Ta có tốc độ truyền sóng:
\(v = \lambda f = 100.500 = 50000cm/s = 500m/s\)
Một sóng có tần số $500 Hz$ và tốc độ lan truyền $350 m/s$. Hỏi hai điểm gần nhất trên phương truyền sóng cách nhau một khoảng bao nhiêu để giữa chúng có độ lệch pha \(\dfrac{\pi }{4}\)?
-
A
$8,75 cm$
-
B
$17,5 cm$
-
C
$35 cm$
-
D
$70 cm$
Đáp án của giáo viên lời giải hay : A
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Bước sóng:
\(\lambda = \dfrac{v}{f} = \dfrac{{350}}{{500}} = 0,7m\)
Để độ lệch pha giữa 2 điểm gần nhất là \(\dfrac{\pi }{4}\)
\( \leftrightarrow \Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{\pi }{4} \to d = \dfrac{\lambda }{8} = \dfrac{{0,7}}{8} = 0,0875m = 8,75cm\)
Một sợi dây đàn hồi rất dài có đầu $A$ dao động với tần số $f$ và theo phương vuông góc với sợi dây. Biên độ dao động là $4 cm$, vận tốc truyền sóng trên dây là $4 (m/s)$. Xét một điểm $M$ trên dây và cách $A$ một đoạn $28 cm$, người ta thấy M luôn luôn dao động lệch pha với $A$ một góc \(\Delta \varphi = (2k + 1)\dfrac{\pi }{2}\) với $k = 0, ±1, ±2,....$. Tính bước sóng $λ$? Biết tần số $f$ có giá trị trong khoảng từ $22 Hz$ đến $26 Hz$.
-
A
$12 cm$
-
B
$8 cm$
-
C
$14 cm$
-
D
$16 cm$
Đáp án của giáo viên lời giải hay : D
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
Độ lệch pha:
\(\begin{array}{l}\Delta \varphi = (2k + 1)\dfrac{\pi }{2} = \dfrac{{2\pi d}}{\lambda }\\ \to f = \left( {2k + 1} \right)\dfrac{v}{{4d}}\end{array}\)
Mặt khác: $22 Hz < f < 26 Hz$
\(\begin{array}{l} \to 22 < f = \left( {2k + 1} \right)\dfrac{v}{{4d}} < 26 \\\leftrightarrow 22 < \left( {2k + 1} \right)\dfrac{4}{{4.0,28}} < 26\\ \to 2,58 < k < 3,14 \\\to k = 3\\ \to f = \left( {2.3 + 1} \right)\dfrac{4}{{4.0,28}} = 25H{\rm{z}} \\\to \lambda {\rm{ = }}\dfrac{v}{f} = \dfrac{4}{{25}} = 0,16m = 16cm\end{array}\)
Một sóng ngang có chu kì $T = 0,2s$ truyền trong một môi trường đàn hồi có tốc độ $1 m/s$. Xét trên phương truyền sóng $Ox$, vào một thời điểm nào đó một điểm $M$ nằm tại đỉnh sóng thì ở trước $M$ theo chiều truyền sóng, cách $M$ một khoảng từ $42cm$ đến $60cm$ có điểm $N$ đang từ vị tri cân bằng đi lên đỉnh sóng . Khoảng cách $MN$ là:
-
A
$50cm$
-
B
$55cm$
-
C
$52cm$
-
D
$45cm$
Đáp án của giáo viên lời giải hay : B
Áp dụng biểu thức tính bước sóng: \(\lambda = vT\)
Bước sóng:
\(\lambda = vT = 1.0,2 = 0,2m\)
Độ lệch pha:
Khi điểm M ở đỉnh sóng, điểm N ở vị trí cân bằng đang đi lên
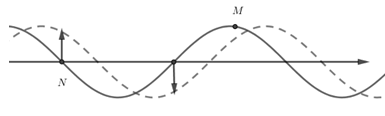
Theo hình vẽ thì khoảng cách MN
\(MN = \dfrac{3}{4}\lambda + k\lambda \) với $k = 0; 1; 2; ...$
\(\begin{array}{l}0,42 < MN = \dfrac{3}{4}\lambda + k\lambda < 0,60 \to 1,35 < k < 2,25\\ \to k = 2\\ \to MN = \dfrac{3}{4}\lambda + 2\lambda = 0,55m = 55cm\end{array}\)
Một dây đàn hồi dài có đầu $A$ dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng trên dây là $4m/s$. Xét một điểm $M$ trên dây và cách $A$ một đoạn $40cm$, người ta thấy $M$ luôn luôn dao động lệch pha so với $A$ một góc \(\Delta \varphi = (k + 0,5)\pi \) với $k$ là số nguyên. Tính tần số, biết tần số $f$ có giá trị trong khoảng từ $8 Hz$ đến $13 Hz$.
-
A
$8,5Hz$
-
B
$10Hz$
-
C
$12Hz$
-
D
$12,5Hz$
Đáp án của giáo viên lời giải hay : D
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Áp dụng biểu thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+ Độ lệch pha giữa $M$ và $A$:
\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi d}}{{\dfrac{v}{f}}} \\\Rightarrow \dfrac{{2\pi df}}{v} = (k + 0,5)\pi \\\Rightarrow f = \left( {k + 0,5} \right)\dfrac{v}{{2d}} = 5\left( {k + 0,5} \right)Hz\)
Theo đầu bài:
\(8Hz < f < 13Hz \\\Rightarrow 8 < \left( {k + 0,5} \right).5 <13\\\Rightarrow 1,1 < k < 2,1 \\\Rightarrow k = 2 \\\Rightarrow f = 12,5Hz\)
Đầu A của một sợi dây dài căng ngang, dao động điều hòa tạo ra một sóng ngang truyền trên sợi dây với biên độ không đổi \(6cm\) và chu kỳ \(2s\). Trên dây, hai điểm dao động ngược pha gần nhau nhất có vị trí cân bằng cách nhau \(30cm\). O và M là hai điểm trên sợi dây có vị trí cân bằng cách nhau \(45cm\) (O gần A hơn M). Tại thời điểm \(t = 0\), điểm O bắt đầu đi lên. Thời điểm đầu tiên điểm M lên đến độ cao \(3cm\) là
-
A
5/3 (s)
-
B
3/2 (s)
-
C
1/6 (s)
-
D
13/6 (s)
Đáp án của giáo viên lời giải hay : A
Độ lệch pha giữa hai điểm trên phương truyền sóng là \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Hai điểm dao động ngược pha gần nhau nhất trên phương truyền sóng là λ/2
Vận tốc \(v = \dfrac{S}{t}\)
Phương trình sóng tại O là:
\({u_O} = A\cos \left( {\omega t + {\varphi _O}} \right) = 6\cos \left( {\pi t - \frac{\pi }{2}} \right)\)
Phương trình sóng tại M là:
\({u_M} = A\cos \left( {\omega t + {\varphi _O} - \frac{{2\pi d}}{\lambda }} \right) = 6\cos \left( {\pi t - \frac{\pi }{2} - \frac{{2\pi .45}}{{60}}} \right)\)
\( \Rightarrow {u_M} = 6\cos \left( {\pi t - 2\pi } \right)\)
Thời điểm M đến vị trí có li độ x = 3cm, ta có:
\({u_M} = 3 \Leftrightarrow 6\cos \left( {\pi t - 2\pi } \right) = 3\)
\( \Leftrightarrow \cos \left( {\pi t - 2\pi } \right) = 0,5\)
\( \Leftrightarrow \left[ \begin{array}{l}\pi t - 2\pi = \frac{\pi }{3}\\\pi t - 2\pi = - \frac{\pi }{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = \frac{7}{3}\left( s \right)\\t = \frac{5}{3}\left( s \right)\end{array} \right.\)
Vậy thời điểm M đến vị trí có li độ x = 3cm lần đầu tiên là \(t = \frac{5}{3}\left( s \right)\)
Một nguồn phát sóng cơ dao động với phương trình \(u = 4\cos \left( {4\pi t - \dfrac{\pi }{4}} \right)\left( {{\rm{cm}}} \right)\). Biết dao động tại hai điểm gần nhau nhất trên cùng một phương truyền sóng cách nhau 0,5m có độ lệch pha là \(\dfrac{\pi }{3}\). Tốc độ truyền của sóng đó là
-
A
1,0 m/s.
-
B
2,0 m/s.
-
C
1,5 m/s.
-
D
6,0 m/s.
Đáp án của giáo viên lời giải hay : D
Độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Vận tốc truyền sóng: \(v = \lambda f = \lambda \dfrac{\omega }{{2\pi }}\)
Độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi df}}{v} = \dfrac{\pi }{3}\)
\( \Rightarrow v = 6df = 6d\dfrac{\omega }{{2\pi }} = 6.0,5.\dfrac{{4\pi }}{{2\pi }} = 6\,\,\left( {m/s} \right)\)
Một nguồn phát sóng nước có dạng \(u = A\cos \left( {\dfrac{\pi }{4}t} \right)\,\,\left( {cm} \right)\). Cho tốc độ truyền sóng không đổi. Tại một điểm cách nguồn một khoảng d, độ lệch pha của dao động sóng tại điểm đó ở hai thời điểm cách nhau \(\Delta t = 0,2\,s\) là
-
A
\(0,05\pi .\)
-
B
\(0,125\pi .\)
-
C
\(0,16\pi .\)
-
D
\(0,24\pi .\)
Đáp án của giáo viên lời giải hay : A
Độ lệch pha theo thời gian: \(\Delta \varphi = \omega \Delta t\)
Độ lệch pha giữa hai thời điểm là: \(\Delta \varphi = \omega \Delta t = \dfrac{\pi }{4}.0,2 = 0,05\pi \,\,\left( {rad} \right)\)
Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần ba bước sóng. Biên độ sóng không đổi trong quá trình truyền. Tại một thời điểm, khi li dộ dao động của phần tử tại M là 3cm thì li độ dao động của phần tử tại N là -3cm. Biên độ dao động sóng bằng
-
A
\(6cm\)
-
B
\(3cm\)
-
C
\(2\sqrt 3 cm\)
-
D
\(3\sqrt 2 cm\)
Đáp án của giáo viên lời giải hay : C
+ Áp dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
+ Sử dụng vòng tròn lượng giác
Độ lệch pha của hai phần tử\(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi \dfrac{\lambda }{3}}}{\lambda } = \dfrac{{2\pi }}{3}\)
Vẽ trên vòng tròn lượng giác, ta có:
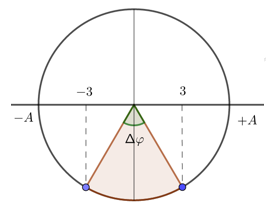
Từ vòng tròn lượng giác, ta có: \(\sin \dfrac{{\Delta \varphi }}{2} = \dfrac{3}{A} \Rightarrow A = \dfrac{3}{{\sin \dfrac{{\Delta \varphi }}{2}}} = \dfrac{3}{{\sin \dfrac{\pi }{3}}} = 2\sqrt 3 cm\)
Bước sóng của một sóng hình sin là quãng đường sóng truyền được trong
-
A
hai giây.
-
B
một giây.
-
C
hai chu kì.
-
D
một chu kì.
Đáp án của giáo viên lời giải hay : D
Sử dụng lí thuyết khái niệm bước sóng.
Bước sóng là quãng đường sóng truyền đường trong một chu kì.
