Ta quan sát thấy hiện tượng gì khi trên dây có sóng dừng?
-
A
Tất cả phần tử dây đều đứng yên.
-
B
Trên dây có những bụng sóng xen kẽ với nút sóng.
-
C
Tất cả các điểm trên dây đều dao động với biên độ cực đại.
-
D
Tất cả các điểm trên dây đều chuyển động với cùng tốc độ.
Đáp án của giáo viên lời giải hay : B
Trong sóng dừng có một số điểm luôn luôn đứng yên gọi là nút, và một số điểm luôn luôn dao động với biên độ cực đại gọi là bụng.
Phát biểu nào sau đây là đúng?
-
A
Khi có sóng dừng trên dây đàn hồi thì tất cả các điểm trên dây đều dừng lại không dao động.
-
B
Khi có sóng dừng trên dây đàn hồi thì nguồn phát sóng ngừng dao động còn các điểm trên dây vẫn dao động.
-
C
Khi có sóng dừng trên dây đàn hồi thì trên dây có các điểm dao động mạnh xen kẽ với các điểm đứng yên.
-
D
Khi có sóng dừng trên dây đàn hồi thì trên dây mọi điểm luôn luôn dao động với biên độ cực đại
Đáp án của giáo viên lời giải hay : C
Khi có sóng dừng thì trên dây xuất hiện những điểm luôn luôn đứng yên gọi là nút, và một số điểm luôn luôn dao động với biên độ cực đại gọi là bụng.
Khi có sóng dừng trên dây, khoảng cách giữa hai nút liên tiếp bằng
-
A
Một số nguyên lần bước sóng.
-
B
Một phần tư bước sóng.
-
C
Một nửa bước sóng.
-
D
Một bước sóng.
Đáp án của giáo viên lời giải hay : C
Khoảng cách giữa 2 nút hoặc 2 bụng liền kề của sóng dừng là $\dfrac{\lambda }{2}$.
Quan sát sóng dừng trên một sợi dây đàn hồi, người ta đo được khoảng cách giữa 5 nút sóng liên tiếp là 100 cm. Biết tần số của sóng truyền trên dây bằng 100 Hz, vận tốc truyền sóng trên dây là:
-
A
50 m/s
-
B
100 m/s
-
C
25 m/s
-
D
75 m/s
Đáp án của giáo viên lời giải hay : A
+ Vận dụng công thức xác định khoảng cách giữa n nút liền kề là $(n - 1)\frac{\lambda }{2}$ .
+ Vận dụng công thức tính vận tốc truyền sóng: $v = \lambda f$
Khoảng cách giữa 5 nút liền kề là
$4\frac{\lambda }{2} = 100 \to \lambda = 50cm = 0,5m$
Vận tốc truyền sóng:
$v = \lambda f = 0,5.100 = 50m/s$
Khi có sóng dừng trên một sợi dây đàn hồi thì khoảng cách giữa hai bụng sóng liên tiếp bằng:
-
A
Hai bước sóng.
-
B
Một bước sóng.
-
C
Một phần tư bước sóng.
-
D
Nửa bước sóng.
Đáp án của giáo viên lời giải hay : D
Khoảng cách giữa 2 nút hoặc 2 bụng liền kề của sóng dừng là $\dfrac{\lambda }{2}$.
Khi có sóng dừng trên một sợi dây đàn hồi, khoảng cách từ một bụng đến nút gần nó nhất bằng:
-
A
Một số nguyên lần bước sóng.
-
B
Một nửa bước sóng.
-
C
Một bước sóng.
-
D
Một phần tư bước sóng.
Đáp án của giáo viên lời giải hay : D
Khoảng cách giữa nút và bụng liền kề là $\dfrac{\lambda }{4}$ .
Trên một sợi dây đàn hồi đang có sóng dừng. Biết khoảng cách ngắn nhất giữa một nút sóng và vị trí cân bằng của một bụng sóng là 0,25m. Sóng truyền trên dây với bước sóng là:
-
A
0,5 m.
-
B
1,5 m.
-
C
1,0 m.
-
D
2,0 m.
Đáp án của giáo viên lời giải hay : C
Vận dụng công thức xác định khoảng cách giữa nút và bụng liền kề là $\frac{\lambda }{4}$ .
Ta có: khoảng cách giữa nút và bụng liền kề là $\frac{\lambda }{4} = 0,25m \to \lambda = 1m$
Sóng dừng xảy ra trên dây đàn hồi cố định có 1 bụng sóng khi:
-
A
Chiều dài của dây bằng một phần tư bước sóng.
-
B
Chiều dài bước sóng gấp đôi chiều dài của dây.
-
C
Chiều dài của dây bằng bước sóng.
-
D
Chiều dài bước sóng bằng một số lẻ chiều dài của dây.
Đáp án của giáo viên lời giải hay : B
Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Có 1 bụng sóng khi k = 1 => λ =2l
Trên một sợi dây có chiều dài l , hai đầu cố định, đang có sóng dừng. Trên dây có một bụng sóng. Biết vận tốc truyền sóng trên dây là v không đổi. Tần số của sóng là:
-
A
$\dfrac{v}{{2\ell }}$
-
B
$\dfrac{v}{{4\ell }}$
-
C
$\dfrac{{2v}}{\ell }$
-
D
$\dfrac{v}{\ell }$
Đáp án của giáo viên lời giải hay : A
Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Điều kiện để có sóng dừng trên dây hai đầu cố định:
$l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k=1
$l = \dfrac{\lambda }{2}{\text{ = }}\dfrac{v}{{2f}} \to f = \dfrac{v}{{2l}}$
Một sợi dây đàn hồi căng ngang, hai đầu cố định. Trên dây có sóng dừng, tốc độ truyền sóng không đổi. Khi tần số sóng trên dây là $42 Hz$ thì trên dây có $4$ điểm bụng. Tính tần số của sóng trên dây nếu trên dây có $6$ điểm bụng.
-
A
$63 Hz$
-
B
$28 Hz$
-
C
$84 Hz$
-
D
$36 Hz$
Đáp án của giáo viên lời giải hay : A
Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ;
Số nút sóng = k + 1
Vì hai đầu cố định là 2 nút nên ta có:
$l=k\dfrac{\lambda }{2}$ $= k\dfrac{v}{{2f}}$ $= k’\dfrac{{\lambda '}}{2}$ $= k’\dfrac{v}{{2f'}}$
=> $f’ =\dfrac{{k'f}}{k}= 63 Hz$
Quan sát sóng dừng trên sợi dây $AB$, đầu $A$ dao động điều hòa theo phương vuông góc với sợi dây (coi $A$ là nút). Với đầu $B$ tự do và tần số dao động của đầu $A$ là $22 Hz$ thì trên dây có $6$ nút. Nếu đầu $B$ cố định và coi tốc độ truyền sóng của dây như cũ, để vẫn có $6$ nút thì tần số dao động của đầu $A$ phải bằng bao nhiêu?
-
A
$44 Hz$
-
B
$20 Hz$
-
C
$33 Hz$
-
D
$24,5 Hz$
Đáp án của giáo viên lời giải hay : B
Vận dụng điều kiện để có sóng dừng trên dây $1$ đầu cố định, $1$ đầu tự do và hai đầu cố định.
+ Hai đầu là nút sóng:
$l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
+ 1 đầu cố định, 1 đầu tự do:
$l = (2k + 1)\dfrac{\lambda }{4}{\text{ }}(k \in N)$
Khi $B$ tự do thì:
$ l = (2k + 1)\dfrac{{{\lambda _1}}}{4}$ $= (2k + 1)\dfrac{v}{{4{f_1}}}$.
Khi $B$ cố định thì:
$l = k\dfrac{{{\lambda _2}}}{2}$$= k\dfrac{v}{{2{f_2}}}$
$f_2 = \dfrac{{2k{f_1}}}{{2k + 1}}$.
Vì trên dây có $6$ nút nên $k = 5$.
Vậy: $f_2=\dfrac{{2.5.22}}{{2.5 + 1}}= 20 (Hz)$
Một sợi dây $AB$ dài $100 cm$ căng ngang, đầu $B$ cố định, đầu $A$ gắn với một nhánh của âm thoa dao động điều hòa với tần số $40 Hz$. Trên dây $AB$ có một sóng dừng ổn định, $A$ được coi là nút sóng. Tốc độ truyền sóng trên dây là $20 m/s$. Tìm số nút sóng và bụng sóng trên dây, kể cả $A$ và $B$.
-
A
$3$ bụng và $4$ nút
-
B
$4$ bụng và $4$ nút
-
C
$4$ bụng và $5$ nút
-
D
$5$ bụng và $5$ nút
Đáp án của giáo viên lời giải hay : C
+ Sử dụng công thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ;
Số nút sóng = k + 1
Ta có:
\(\lambda = \dfrac{v}{f} = 0.5{\text{ }}m = 50{\text{ }}cm.\)
Ta có điều kiện để có sóng dừng trên dây hai đầu cố định:
$l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ;
Số nút sóng = k + 1
Trên dây có:
\(k = \dfrac{{AB}}{{\dfrac{\lambda }{2}}} = \dfrac{{2AB}}{\lambda } = 4\) bụng sóng.
=> số nút = k + 1 = 5 nút sóng
Trên một sợi dây dài 0,9 m có sóng dừng. Kể cả hai nút ở hai đầu dây thì trên dây có 10 nút sóng. Biết tần số của sóng truyền trên dây là 200Hz. Sóng truyền trên dây có tốc độ là
-
A
90 cm/s
-
B
40 m/s
-
C
40 cm/s
-
D
90 m/s
Đáp án của giáo viên lời giải hay : B
+ Sử dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\)
+Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
Ta có điều kiện để có sóng dừng trên dây hai đầu cố định:
$l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
$l = k\frac{\lambda }{2} \leftrightarrow 0,9 = 9\frac{\lambda }{2} \to \lambda = 0,2m$
tốc độ truyền sóng trên dây:
\(v = \lambda f = 0,2.200 = 40m/s\)
Một sợi dây $AB$ dài $50 cm$. Đầu $A$ dao động với tần số $f = 50 Hz$. Đầu $B$ cố định. Trên dây $AB$ có một sóng dừng ổn định, $A$ được coi là nút sóng. Tốc độ truyền sóng trên dây là $1 m/s$. Hỏi điểm $M$ cách $A$ một khoảng $3,5 cm$ là nút hay bụng thứ mấy kể từ $A$ và trên dây có bao nhiêu nút, bao nhiêu bụng kể cả $A$ và $B$.
-
A
M là nút số $4$, trên dây có $50$ nút - $50$ bụng.
-
B
M là bụng số $4$, trên dây có $50$ nút - $50$ bụng.
-
C
M là nút số $4$, trên dây có $50$ nút - $51$ bụng.
-
D
M là bụng số $4$, trên dây có $51$ nút - $50$ bụng.
Đáp án của giáo viên lời giải hay : D
+ Sử dụng công thức tính bước sóng: \(\lambda = \dfrac{v}{f}\)
+Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
Ta có:
\(\lambda = \dfrac{v}{f} = 0,02{\text{ }}m = 2{\text{ }}cm\)
Ta có điều kiện để có sóng dừng trên dây hai đầu cố định:
$l = k\dfrac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
\(AM = 3,5{\text{ }}cm{\text{ }} = 7\dfrac{\lambda }{4} = \left( {2.3{\text{ }} + {\text{ }}1} \right)\dfrac{\lambda }{4}\)
=> M là bụng số $4$
$l = k\dfrac{\lambda }{2}{\text{ }} \leftrightarrow 0,5 = {\text{k}}\dfrac{{0,02}}{2} \to k = 50$
=> Trên dây có $50$ bụng, $51$ nút
Một sợi dây đàn hồi, hai đầu cố định có sóng dừng. Khi tần số sóng trên dây là 20 Hz thì trên dây có 3 bụng sóng. Muốn trên dây có 4 bụng sóng thì phải
-
A
Tăng tần số thêm \(\frac{{20}}{3}\) Hz
-
B
Giảm tần số đi 10 Hz.
-
C
Tăng tần số thêm 30 Hz.
-
D
Giảm tần số đi còn \(\frac{{20}}{3}\) Hz
Đáp án của giáo viên lời giải hay : A
+Vận dụng điều kiện để có sóng dừng trên dây hai đầu cố định: $l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
Ta có điều kiện để có sóng dừng trên dây hai đầu cố định:
$l = k\frac{\lambda }{2}{\text{ }}(k \in {N^*})$
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
$l = k\frac{\lambda }{2} = k\frac{v}{{2f}} \to f = \frac{{kv}}{{2l}}$
+ Khi k = 3:
${f_1} = \frac{{3v}}{{2l}}$
+ Khi k = 4:
${f_2} = \frac{{4v}}{{2l}}$
$\begin{gathered}\to \frac{{{f_1}}}{{{f_2}}} = \frac{3}{4} \to {f_2} = \frac{4}{3}{f_1} = \frac{4}{3}.20 =\frac{{80}}{3}H{\text{z}} \hfill \\\to {f_2} - {f_1} = \frac{{80}}{3} - 20 = \frac{{20}}{3}H{\text{z}} \hfill \\\end{gathered} $
=> Tăng tần số thêm 20/3 Hz
Trong ống sáo một đầu kín một đầu hở có sóng dừng với tần số cơ bản là 110 Hz. Biết tốc độ truyền âm trong không khí là 330 m/s. Tìm độ dài của ống sáo.
-
A
3 m
-
B
1,5 m
-
C
0,75 m
-
D
2,25 m
Đáp án của giáo viên lời giải hay : C
+ Sử dụng công thức tính bước sóng: \(\lambda = \frac{v}{f}\)
+Vận dụng điều kiện để có sóng dừng trên dây 1 đầu cố định, 1 đầu tự do:
$l = (2k + 1)\frac{\lambda }{4}{\text{ }}(k \in N)$
Ta có:
λ = \(\dfrac{v}{f}\) =3 m.
Đầu kín của ống sáo là nút, đầu hở là bụng của sóng dừng nên chiều dài của ống sáo là:
L = \(\dfrac{\lambda }{4}\) = 0,75 m.
Quan sát trên một sợi dây thấy có sóng dừng với biên độ của bụng sóng là $a$. Tại điểm trên sợi dây cách bụng sóng một phần tư bước sóng có biên độ dao động bằng:
-
A
$a/2$
-
B
$0$
-
C
$a/4$
-
D
$a$
Đáp án của giáo viên lời giải hay : B
Sử dụng lí thuyết về phương trình sóng dừng:
${u_M} = 2Ac{\text{os}}(2\pi \dfrac{d}{\lambda })c{\text{os}}(2\pi ft)$
Ta có:
${A_M} = 2a\left| {{\text{cos}}(2\pi \dfrac{d}{\lambda })} \right|$
$ \to d = \dfrac{\lambda }{4} \to {A_M} = 2a\left| {{\text{cos}}(2\pi \dfrac{1}{4})} \right| = 0$
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, $A$ là một điểm nút, $B$ là một điểm bụng gần $A$ nhất, $C$ là trung điểm của $AB$, với $AC = 10cm$. Biết khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại $B$ bằng biên độ dao động của phần tử tại $C$ là $0,1s$. Tốc độ truyền sóng trên dây là:
-
A
$2 m/s$
-
B
$0,5 m/s$
-
C
$0,25 m/s$
-
D
$1 m/s$
Đáp án của giáo viên lời giải hay : A
- Khoảng cách giữa trung điểm của một nút và bụng gần nhất với nút đó là: $\dfrac{\lambda }{8}$
- Khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại bụng sóng bằng biên độ dao động của phần tử tại trung điểm của bụng và nút sóng liền kề là: $\dfrac{T}{4}$
- Áp dụng công thức tính vận tốc truyền sóng: $v = \dfrac{\lambda }{T}$
Vì $B$ là điểm bụng gần nút $A$ nhất
$C$- là trung điểm của $AB$ =>
$AC = \dfrac{\lambda }{8} = 10cm \to \lambda = 80cm$
Biên độ dao động của phần tử tại $C$:
${A_C} = \sqrt 2 A$
Khoảng thời gian ngắn nhất giữa hai lần mà li độ dao động của phần tử tại $B$ bằng biên độ dao động của phần tử tại $C$ là:
$\dfrac{T}{4} = 0,1{\text{s}} \to T = 0,4{\text{s}}$
Vận tốc truyền sóng:
$v = \dfrac{\lambda }{T} = \dfrac{{0,8}}{{0,4}} = 2m/s$
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây $A$ là một điểm nút, $B$ là một điểm bụng gần $A$ nhất, $AB = 14 cm$, gọi $C$ là một điểm trong khoảng $AB$ có biên độ bằng một nửa biên độ của $B$. Khoảng cách $AC$ là:
-
A
$14/3$
-
B
$7$
-
C
$3,5$
-
D
$1,75$
Đáp án của giáo viên lời giải hay : A
Áp dụng công thức tính biên độ sóng dừng: \({a_C} = 2asin\dfrac{{2\pi d}}{\lambda }\)
Giả sử biểu thức sóng tại nguồn $O$ (cách $A$: $OA = l$) $u = acosωt$
Xét điểm $C$ cách $A$: $CA = d$. Biên độ của sóng dừng tại $C$:
\({a_C} = 2asin\dfrac{{2\pi d}}{\lambda }\)
Để $a_C = a$ (bằng nửa biện độ của $B$ là bụng sóng):
\(sin\dfrac{{2\pi d}}{\lambda } = 0,5\)
\( \to d = (\dfrac{1}{{12}} + {\text{ }}k)\lambda \) Với $λ = 4AB = 56cm.$
Điểm $C$ gần $A$ nhất ứng với $k = 0$
$d = AC = λ/12 = 56/12 = 14/3 cm.$
Một dây đàn hồi $AB$ đầu $A$ được rung nhờ một dụng cụ để tạo thành sóng dừng trên dây, biết Phương trình dao động tại đầu $A$ là $u_A= acos100πt$. Quan sát sóng dừng trên sợi dây ta thấy trên dây có những điểm không phải là điểm bụng dao động với biên độ $b$ \((b \ne 0)\) cách đều nhau và cách nhau khoảng $1m$. Giá trị của $b$ và tốc truyền sóng trên sợi dây lần lượt là:
-
A
\(a\sqrt 2 \); $v = 200m/s$
-
B
\(a\sqrt 3 \); $v =150m/s$
-
C
$a; v = 300m/s$
-
D
\(a\sqrt 2 \); $v =100m/s$
Đáp án của giáo viên lời giải hay : A
+ Sử dụng vòng tròn lượng giác
+ Áp dụng công thức tính tốc độ truyền sóng: $v = λf$
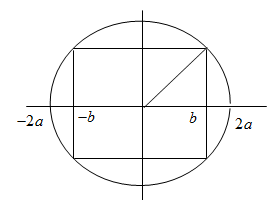
Các điểm dao động với biên độ \(b \ne 0\) và \(b \ne 2a\) (tức là không phải là điểm nút và điểm bụng) cách đều nhau thì khoảng cách giữa hai điểm bằng $\dfrac{\lambda }{4} = 1m \to \lambda = 4m$
Do đó $v = λf = 4.50 = 200 (m/s)$
Theo hình vẽ ta thấy
\(b =\dfrac{{2a\sqrt 2 }}{2}= a\sqrt 2 \)
(Biên độ của bụng sóng là $2a$)
Một sợi dây căng ngang với hai đầu cố định, đang có sóng dừng. Biết khoảng cách xa nhất giữa hai phần tử dây dao động với cùng biên độ 5 mm là 80 cm, còn khoảng cách xa nhất giữa hai phần tử dây dao động cùng pha với cùng biên độ 5 mm là 65 cm. Tỉ số giữa tốc độ cực đại của một phần tử dây tại bụng sóng và tốc độ truyền sóng trên dây là
-
A
0,12.
-
B
0,41.
-
C
0,21.
-
D
0,14.
Đáp án của giáo viên lời giải hay : A
Sử dụng lí thuyết về sóng dừng trên dây hai đầu cố định
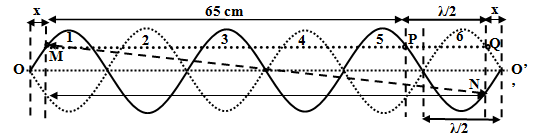
+ Các điểm thuộc cùng một bó sóng dao động cùng pha nhau, các điểm thuộc bó sóng lẻ dao động ngược pha với các điểm thuộc bó sóng chẵn.
+ Khoảng cách xa nhất giữa hai phần tử dây dao động cùng biên độ 5 mm ở hai bó sóng ngoài cùng (cùng cách mỗi đầu cố định một khoảng x) là: MN = 80cm.
+ Khoảng cách xa nhất giữa hai phần tử dây dao động cùng pha cùng biên độ 5 mm là: MP = 65 cm.
+ Dễ dàng nhận thấy: \(PQ = \dfrac{\lambda }{2}\)
=> \(PQ = \dfrac{\lambda }{2} = MQ - MP = \sqrt {M{N^2} - Q{N^2}} - MP = \sqrt {{{80}^2} - {1^2}} - 65 \approx 15cm = > \lambda \approx 30cm.\)
+ Ta có \((MQ = 79,99 \approx 80cm)\) (: \(\dfrac{{MQ}}{{\lambda /2}} = \dfrac{{80}}{{15}} = 5 + \dfrac{1}{3}\)
=> Trên sợi dây có 6 bó sóng. (Có \(\dfrac{1}{3}.\dfrac{\lambda }{2} + 2x = \dfrac{\lambda }{2})\)
+ Chiều dài sợi dây là: \(\ell = OO' = \dfrac{\lambda }{2} = 90cm \Rightarrow x = \dfrac{{OO' - MQ}}{2} = \dfrac{{90 - 80}}{2} = 5cm.\)
+ Biên độ sóng tại điểm M cách nút sóng 1 khoảng x là: \({A_M} = 2.a\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| = 2a.\sin \dfrac{{2\pi .5}}{{30}} = a\sqrt 3 = 5mm.\)
=> \(a = \dfrac{{0,5}}{{\sqrt 3 }}(cm)\)
=> Biên độ bụng sóng là: \(2a = \dfrac{1}{{\sqrt 3 }}(cm)\)
+ Tốc độ cực đại của phần tử tại bụng sóng: vmax = 2aω = \(\dfrac{1}{{\sqrt 3 }}\)2πf (cm/s).
+ Tốc độ truyền sóng trên dây: \(v = λf = 30f (cm/s)\)
+ Tỉ số: \(\dfrac{{{v_{\max }}}}{v} = \dfrac{{2\pi }}{{\sqrt 3 .30}} \approx \)\(0,12086\).
Sóng truyền trên một sợi dây đàn hồi có hai đầu cố định với bước sóng λ. Để trên dây có sóng dừng thì chiều dài của sợi dây bằng
-
A
\((2k + 1)\dfrac{\lambda }{2}\) với k = 0; 1; 2; …
-
B
\(k\dfrac{\lambda }{2}\) với k = 1; 2; 3;…
-
C
\((2k + 1)\dfrac{\lambda }{4}\) với k = 0; 1; 2; …
-
D
\(k\dfrac{\lambda }{4}\) với k = 1; 2; 3;…
Đáp án của giáo viên lời giải hay : B
Điều kiện xảy ra sóng dừng trên dây có hai đầu cố định: \(k\dfrac{\lambda }{2}\) với k = 1; 2; 3;…
M, N và P là 3 vị trí cân bằng liên tiếp trên một sợi dây đang có sóng dừng mà các phần tử tại đó dao động với cùng biên độ bằng \(\sqrt 3 cm\). Biết vận tốc tức thời của hai phần tử tại N và P thỏa mãn \({v_N}.{v_P} \ge 0\); \(MN = 40cm\), \(NP = 20cm\), tần số góc của sóng là \(20rad/s\). Tốc độ dao động của phần tử tại trung điểm của NP khi sợi dây có dạng một đoạn thẳng bằng
-
A
\(40cm/s\)
-
B
\(20cm/s\)
-
C
\(20\sqrt 3 cm/s\)
-
D
\(40\sqrt 3 cm/s\)
Đáp án của giáo viên lời giải hay : A
Sử dụng biểu thức tính biên độ sóng dừng: \(A = {A_b}\sin \dfrac{{\pi d}}{\lambda }\) với \(d\) khoảng cách từ điểm đó đến nút
Ta có M, N, P là các vị trí cân bằng liên tiếp có cùng biên độ và \({v_N}.{v_P} \ge 0\)
Ta suy ra: N và P nằm trên một bó sóng: \(\dfrac{\lambda }{4} = \dfrac{1}{2}\left( {MN + NP} \right) = 30cm\)
\( \Rightarrow \lambda = 120cm\)
Lại có, biên độ: \(A = {A_b}\sin \dfrac{{2\pi d}}{\lambda } = \sqrt 3 cm\) (với \(d\) khoảng cách tới nút)
Ta suy ra: \({A_b}\sin \dfrac{{2\pi .20}}{{120}} = \sqrt 3 \Rightarrow {A_b} = 2 cm\)
Vận tốc của phần tử tại trung điểm N, P khi dây duỗi thẳng là vận tốc khi qua vị trí cân bằng
\(v = {v_{max}} = {A_b}.\omega = 2 .20 = 40 \left( {cm/s} \right)\)
Một sợi dây đàn hồi căng ngang với hai đầu cố định. Sóng truyền trên dây có tốc độ không đổi nhưng tần số f thay đổi được. Khi f nhận giá trị 1760 Hz thì trên dây có sóng dừng với 4 bụng sóng. Giá trị nhỏ nhất của f bằng bao nhiêu để trên dây vẫn có sóng dừng?
-
A
880 Hz.
-
B
400 Hz.
-
C
440 Hz.
-
D
800 Hz.
Đáp án của giáo viên lời giải hay : C
Tần số trên dây với n bó sóng: \(f = n.{f_0}\)
Tần số trên dây với n bó sóng là: \(f = n.{f_0}\)
Trên dây có 4 bụng sóng → có 4 bó sóng, tần số tương ứng là: \(1760 = 4{f_0} \Rightarrow {f_0} = 440\left( {Hz} \right)\)
Để giá trị tần số nhỏ nhất mà trên dây vẫn còn sóng dừng, số bó sóng trên dây là nhỏ nhất:
\({n_{\min }} = 1 \Rightarrow {f_{\min }} = 1.{f_0} = 1.440 = 440\,\,\left( {Hz} \right)\)
Một sợi dây đàn hồi OM dài 120 cm có hai đầu cố định. Khi được kích thích dao động, trên dây hình thành hai bụng sóng (với O và M là hai nút), biên độ tại bụng là A. Tại điểm P gần O nhất dao động với biên độ \(\dfrac{A}{2}\) là
-
A
5 cm
-
B
10 cm
-
C
15 cm
-
D
20 cm
Đáp án của giáo viên lời giải hay : B
Điều kiện có sóng dừng với hai đầu dây cố định: \({\rm{l}} = k\dfrac{\lambda }{2}\) với k là số bụng sóng
Biên độ của điểm cách nút sóng khoảng x: \({A_M} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right|\)
Trên dây hình thành 2 bụng sóng, ta có:
\({\rm{l}} = k\dfrac{\lambda }{2} \Rightarrow 120 = 2.\dfrac{\lambda }{2} \Rightarrow \lambda = 120\,\,\left( {cm} \right)\)
Biên độ của điểm P là:
\(\begin{array}{l}{A_P} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| \Rightarrow \dfrac{A}{2} = A.\left| {\sin \dfrac{{2\pi x}}{{120}}} \right|\\ \Rightarrow \left| {\sin \dfrac{{2\pi x}}{{120}}} \right| = \dfrac{1}{2} \Rightarrow x = 10\,\,\left( {cm} \right)\end{array}\)
Để đo tốc độ truyền sóng v trên một sợi dây đàn hồi AB, người ta nối đầu A vào một nguồn dao động số tần số \(f = 100\,\,Hz \pm 0,02\% \). Đầu B được gắn cố định. Người ta đo khoảng cách giữa hai điểm trên dây gần nhất không dao động với kết quả \(d = 0,02\,\,m \pm 0,82\% \). Tốc độ truyền sóng trên sợi dây AB là
-
A
\(v = 4\,\,m/s \pm 0,84\% \)
-
B
\(v = 2\,\,m/s \pm 0,016\% \)
-
C
\(v = 2\,\,m/s \pm 0,84\% \)
-
D
\(v = 4\,\,m/s \pm 0,016\% \)
Đáp án của giáo viên lời giải hay : A
Khoảng cách giữa hai điểm gần nhất không dao động: \({\rm{l}} = \dfrac{\lambda }{2}\)
Tốc độ truyền sóng trên dây: \(\overline v = \overline \lambda \overline f \)
Sai số tỉ đối: \(\dfrac{{\Delta v}}{{\overline v }} = \dfrac{{\Delta \lambda }}{{\overline \lambda }} + \dfrac{{\Delta f}}{{\overline f }}\)
Tốc độ truyền sóng trên dây trung bình là: \(\overline v = \overline \lambda \overline f = 2\overline {\rm{l}} \overline f = 2.0,02.100 = 4\,\,\left( m \right)\)
Do \({\rm{l}} = \dfrac{\lambda }{2} \Rightarrow \dfrac{{\Delta {\rm{l}}}}{{\overline {\rm{l}} }} = \dfrac{{\Delta \lambda }}{{\overline \lambda }}\)
Sai số tỉ đối là: \(\delta = \dfrac{{\Delta v}}{{\overline v }} = \dfrac{{\Delta \lambda }}{{\overline \lambda }} + \dfrac{{\Delta f}}{{\overline f }} = \dfrac{{\Delta {\rm{l}}}}{{\overline {\rm{l}} }} + \dfrac{{\Delta f}}{{\overline f }} = 0,82\% + 0,02\% = 0,84\% \)
Vậy tốc độ truyền sóng trên dây là: \(v = 4\,\,m/s \pm 0,84\% \)
Trong giờ thực hành hiện tượng sóng dừng trên dây với hai đầu cố định, một học sinh thực hiện như sau: tăng tần số của máy phát dao động thì thấy rằng khi sóng dừng xuất hiện trên dây tương ứng với 1 bó sóng và 7 bó sóng thì tần số thu được thỏa mãn \({f_7} - {f_1} = 150\,\,\left( {Hz} \right)\). Khi trên dây xuất hiện sóng dừng với 4 nút sóng thì máy phát tần số hiện giá trị là
-
A
100 Hz
-
B
75 Hz
-
C
120 Hz
-
D
125 Hz
Đáp án của giáo viên lời giải hay : B
Điều kiện để có sóng dừng khi hai đầu là nút: \({\rm{l}} = k\dfrac{\lambda }{2} = k\dfrac{v}{{2{f_k}}}\) với k là số bó sóng, k+1 là số nút.
Khi trên dây có 1 bó sóng, ta có chiều dài dây là: \({\rm{l}} = \dfrac{v}{{2{f_1}}}\)
Khi trên dây có 7 bó sóng, chiều dài dây là: \({\rm{l}} = 7\dfrac{v}{{2{f_7}}}\)
\( \Rightarrow {\rm{l}} = 7\dfrac{v}{{2{f_7}}} = \dfrac{v}{{2{f_1}}} = \dfrac{{6v}}{{2\left( {{f_7} - {f_1}} \right)}} \Rightarrow {f_1} = \dfrac{{{f_7} - {f_1}}}{6} = \dfrac{{150}}{6} = 25\,\,\left( {Hz} \right)\)
Khi trên dây có 4 nút sóng, số bó sóng trên dây là 3, khi đó ta có:
\({\rm{l}} = 3\dfrac{v}{{2{f_3}}} = \dfrac{v}{{2{f_1}}} \Rightarrow {f_3} = 3{f_1} = 3.25 = 75\,\,\left( {Hz} \right)\)
Trên một sợi dây đàn hồi căng ngang có ba điểm A, B và C sao cho AB = 1cm, BC = 7cm. Khi sóng dừng hình thành trên sợi dây với bước sóng \(\lambda = 12cm\)và tần số f = 50Hz thì A là một nút sóng, B và C cùng dao động điều hòa theo phương thẳng đứng. Gọi d1 và d2 lần lượt là khoảng cách lớn nhất giữa A với B, và khoảng cách lớn nhất giữa A với C. Biết biên độ của điểm bụng là \({a_B} = 2cm\), tỉ số \(\dfrac{{{d_2}}}{{{d_1}}}\) bằng
-
A
2
-
B
\(2\sqrt 5 \)
-
C
5,8
-
D
4
Đáp án của giáo viên lời giải hay : C
+ Công thức tính biên độ: \(a = {A_B}.\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|\)
Trong đó d là khoảng cách từ điểm ta xét đến nút sóng.
+ Áp dụng định lí Pitago.
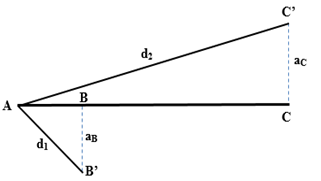
Biên độ của sóng tại B và C:
\(\left\{ \begin{array}{l}{a_B} = {A_B}.\left| {\sin \dfrac{{2\pi .AB}}{\lambda }} \right| = 2.\left| {\sin \dfrac{{2\pi .1}}{{12}}} \right| = 1cm\\{a_C} = {A_B}.\left| {\sin \dfrac{{2\pi .AC}}{\lambda }} \right| = 2.\left| {\sin \dfrac{{2\pi .8}}{{12}}} \right| = \sqrt 3 cm\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}{d_1} = \sqrt {A{B^2} + a_B^2} = \sqrt {{1^2} + {1^2}} = \sqrt 2 cm\\{d_2} = \sqrt {A{C^2} + a_C^2} = \sqrt {{8^2} + {{\left( {\sqrt 3 } \right)}^2}} = \sqrt {67} cm\end{array} \right. \Rightarrow \dfrac{{{d_2}}}{{{d_1}}} = 5,8\)
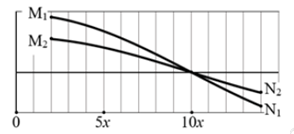
Hình vẽ bên mô phỏng một đoạn của một sợi dây đang có sóng dừng ổn định với bước sóng \(\lambda = 50cm\) ở hai thời điểm khác nhau. Đường cong \({M_1}{N_1}\) là đoạn sợi dây ở thời điểm thứ nhất, đường cong \({M_2}{N_2}\) là đoạn dây đó ở thời điểm thứ hai. Biết tỉ lệ các khoảng cách \(\dfrac{{{M_1}{M_2}}}{{{N_1}{N_2}}} = \dfrac{8}{5}\) . Giá trị của \(x\) trên hình vẽ xấp xỉ là
-
A
\(1,28cm.\)
-
B
\(3,97cm.\)
-
C
\(0,64cm.\)
-
D
\(1,82cm.\)
Đáp án của giáo viên lời giải hay : A
+ Đọc đồ thị
+ Sử dụng biểu thức tính biên độ sóng dừng cách nút một khoảng d: \(A = {A_0}\sin \left( {\dfrac{{2\pi d}}{\lambda }} \right)\)
Từ hình vẽ, dễ thấy khoảng cách nhỏ nhất từ các đầu dây M, N đến một nút sóng lần lượt là \(8x\) và \(4x\), nên biên độ dao động của các phần tử tại hai điểm này lần lượt là
\({A_M} = {A_0}\sin \left( {\dfrac{{2\pi 8x}}{\lambda }} \right)\)
\({A_N} = {A_0}\sin \left( {\dfrac{{2\pi 4x}}{\lambda }} \right)\)
Trong đó, \({A_0}\) là biên độ dao động của bụng sóng.
Hai điểm M, N thuộc hai bó sóng cạnh nhau nên dao động ngược pha nhau:
\(\begin{array}{l}\dfrac{{{u_M}}}{{{A_M}}} = - \dfrac{{{u_N}}}{{{A_N}}}\\ \Rightarrow \dfrac{{{u_{{M_1}}} - {u_{{M_2}}}}}{{{A_M}}} = \dfrac{{{u_{{N_2}}} - {u_{{N_1}}}}}{{{A_N}}}\end{array}\)
Theo đầu bài, ta có: \(\dfrac{{{u_{{M_1}}} - {u_{{M_2}}}}}{{{u_{{N_2}}} - {u_{{N_1}}}}} = \dfrac{{{M_1}{M_2}}}{{{N_1}{N_2}}} = \dfrac{8}{5}\)
\(\begin{array}{l} \Rightarrow \dfrac{{{A_M}}}{{{A_N}}} = \dfrac{{{A_0}\sin \left( {\dfrac{{2\pi 8x}}{\lambda }} \right)}}{{{A_0}\sin \left( {\dfrac{{2\pi 4x}}{\lambda }} \right)}} = \dfrac{8}{5}\\ \Rightarrow \dfrac{{\sin \left( {\dfrac{{2\pi 8x}}{{50}}} \right)}}{{\sin \left( {\dfrac{{2\pi 4x}}{{50}}} \right)}} = \dfrac{8}{5}\\ \Rightarrow x = 1,28cm\end{array}\)
Xét một sóng cơ truyền trên một dây đàn hồi rất dài có bước sóng λ. Sau 1s, sóng truyền được quãng đường bằng L. Tần số của sóng này bằng
-
A
λ + L.
-
B
$\frac{L}{\lambda }.$
-
C
$\frac{\lambda }{L}.$
-
D
λL.
Đáp án của giáo viên lời giải hay : B
Tần số của sóng: $f=\frac{v}{\lambda }.$
Vận tốc của sóng là: $v=\frac{s}{t}=\frac{L}{1}=L$
Tần số của sóng là: $f=\frac{v}{\lambda }=\frac{L}{\lambda }.$
Sóng dừng trên một sợi dây với hai đầu cố định. Khi tần số sóng là \(f\) thì trên sợi dây có 10 nút sóng (kể cả hai đầu). Nếu tần số sóng là \(\frac{4}{3}f\) thì trên dây có số bụng sóng là
-
A
13
-
B
12
-
C
14
-
D
11
Đáp án của giáo viên lời giải hay : B
Sóng dừng với hai đầu cố định: \(l = k\frac{v}{{2f}}\)
Khi tần số sóng là \(f\) thì \(l = k\dfrac{v}{{2f}} \Rightarrow \dfrac{v}{{2l}} = \dfrac{k}{f} = \dfrac{9}{f}\) (1)
Khi tần số là \(\dfrac{4}{3}f\) thì: \(\dfrac{v}{{2l}} = \dfrac{{3k}}{{4f}}\)(2)
Từ (1) và (2) ta có: \(\dfrac{9}{f} = \dfrac{{3k}}{{4f}} \Rightarrow k = 12\)
Một sợi dây đàn hồi dài 1,2m được treo lơ lửng trên một cần rung. Cần rung có thể dao động theo phương ngang với tần số thay đổi được từ 50Hz đến 75Hz. Tốc độ truyền sóng trên dây là 6m/s. Xem đầu nối với cần rung là nút sóng khi có sóng dừng trên dây. Trong quá trình thay đổi tần số rung, số lần tạo ra sóng dừng trên dây là
-
A
11.
-
B
13.
-
C
12.
-
D
10.
Đáp án của giáo viên lời giải hay : D
+ Điều kiện có sóng dừng trên dây 1 đầu cố định, 1 đầu tự do: \(l = \left( {2k + 1} \right)\frac{\lambda }{4}\)
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \frac{v}{f}\)
Khi có sóng dừng chiều dài dây thỏa mãn biểu thức
\(l = \left( {2k + 1} \right)\frac{\lambda }{4} = \left( {2k + 1} \right)\frac{v}{{4f}} \Rightarrow f = \left( {2k + 1} \right)\frac{v}{{4l}} = \left( {2k + 1} \right)\frac{5}{4}\)
Theo đề bài \(50 \le f \le 75\)
\(\begin{array}{l} \Leftrightarrow 50 \le \left( {2k + 1} \right)\frac{5}{4} \le 75 \Leftrightarrow 19,5 \le k \le 29,5\\ \Rightarrow k = 20,21,22,23,24,25,26,27,28,29\end{array}\)
Có 10 giá trị của k
\( \Rightarrow \) Trong quá trình thay đổi tần số rung, số lần tạo ra sóng dừng trên dây là 10 lần.
Đề thi THPT QG - 2020
Một sợi dây dài 96 cm căng ngang, có hai đầu A và B cố định. M và N là hai điểm trên dây với MA = 51 cm và NA = 69 cm. Trên dây có sóng dừng với số bụng nằm trong khoảng từ 5 bụng đến 19 bụng. Biết phần tử dây tại M và N dao động cùng pha và cùng biên độ. Gọi d là khoảng cách từ M đến điểm bụng gần nó nhất. Giá trị của d gần nhất với giá trị nào sau đây?
-
A
4,7 cm
-
B
1,7 cm
-
C
3,2 cm
-
D
6,2 cm.
Đáp án của giáo viên lời giải hay : B
Xét bài toán phụ: Điều kiện để M và N dao động cùng pha và cùng biên độ
M cùng pha và cùng biên độ với các điểm \({N_1},{N_2},...\)
Xét các điểm \({N_1},{N_3},{N_5}\): \(\left\{ \begin{array}{l}A{N_1} + AM = 1\frac{\lambda }{2}\\A{N_3} + AM = 3\frac{\lambda }{2}\end{array} \right.\) \( \Rightarrow \) Tổng quát: \(AN + AM = {k_1}\frac{\lambda }{2}\) (với \({k_1} = 1,3,5,....\) )
Xét các điểm \({N_2},{N_4},{N_6}\): \(\left\{ \begin{array}{l}A{N_2} - AM = 2\frac{\lambda }{2}\\A{N_4} - AM = 4\frac{\lambda }{2}\end{array} \right.\) \( \Rightarrow \) Tổng quát: \(AN - AM = {k_2}\frac{\lambda }{2}\) (với \({k_2} = 2,4,6,....\) )
Xét bài toán: Điều kiện để M và N dao động cùng pha và cùng biên độ
M cùng pha và cùng biên độ với các điểm \({N_1},{N_2},...\)
Xét các điểm \({N_1},{N_3},{N_5}\): \(\left\{ \begin{array}{l}A{N_1} + AM = 1\frac{\lambda }{2}\\A{N_3} + AM = 3\frac{\lambda }{2}\end{array} \right.\) \( \Rightarrow \) Tổng quát: \(AN + AM = {k_1}\frac{\lambda }{2}\) (với \({k_1} = 1,3,5,....\) )
Xét các điểm \({N_2},{N_4},{N_6}\): \(\left\{ \begin{array}{l}A{N_2} - AM = 2\frac{\lambda }{2}\\A{N_4} - AM = 4\frac{\lambda }{2}\end{array} \right.\) \( \Rightarrow \) Tổng quát: \(AN - AM = {k_2}\frac{\lambda }{2}\) (với \({k_2} = 2,4,6,....\) )
Quay về bài:
+ Gọi số bó sóng trên dây: \(k\) \(\left( {5 \le k \le 19} \right)\), ta có: \(l = k\frac{\lambda }{2}\) \( \Rightarrow \frac{\lambda }{2} = \frac{l}{k} = \frac{{96}}{k}\) với \(\left( {5 \le k \le 19} \right)\)
+ Điều kiện để M và N cùng pha và cùng biên độ là:
\(\left[ \begin{array}{l}AN + AM = {k_1}\frac{\lambda }{2} = 120cm\\AN - AM = {k_2}\frac{\lambda }{2} = 18cm\end{array} \right.\) (với \({k_1} = 1,3,5,....\) và \({k_2} = 2,4,6,....\))\( \Rightarrow \left[ \begin{array}{l}{k_1} = \frac{{120}}{{\frac{\lambda }{2}}} = \frac{{5k}}{4}\\{k_2} = \frac{{18}}{{\frac{\lambda }{2}}} = \frac{{3k}}{{16}}\end{array} \right.\)
Thay \(k = 5,6,...,19\) vào 2 biểu thức trên, ta được bảng:
|
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
(lẻ) |
6,25 |
7,5 |
8,75 |
10 |
11,25 |
12,5 |
13,75 |
15 |
16,25 |
17,5 |
18,75 |
20 |
21,25 |
22,5 |
23,75 |
|
(chẵn) |
0,94 |
1,13 |
1,31 |
1,5 |
1,69 |
1,88 |
2,06 |
2,25 |
2,44 |
2,63 |
2,81 |
3 |
3,19 |
3,38 |
3,56 |
Chỉ có \(\left\{ \begin{array}{l}k = 12\\{k_1} = 15\end{array} \right.\) thỏa mãn \(\frac{\lambda }{2} = \frac{{96}}{{12}} = 8cm\)
\(MA = 51cm = 6\frac{\lambda }{2} + 3cm\) \( \Rightarrow M\) cách nút sóng \(3cm\) \( \Rightarrow \) M cách bụng gần nhất: \(4 - 3 = 1cm\)
(Do khoảng cách giữa 1 nút à 1 bụng gần nhất là \(\frac{\lambda }{4} = 4cm\))
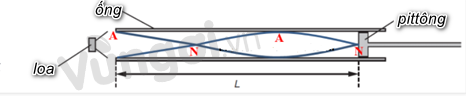
Ống dài hở một đầu. Nó được đóng ở đầu kia bằng một piston có thể di chuyển được dọc theo ống, như hình vẽ. Loa tạo ra âm thanh có tần số 550Hz được đặt gần đầu hở của ống. Piston được dịch chuyển dọc theo ống và nghe thấy âm thanh lớn ở đầu hở khi khoảng cách L giữa piston và đầu hở của ống là 45cm. Tốc độ âm thanh trong ống bằng \(330m.{s^{ - 1}}\). Xác định tần số thấp nhất mà âm phát ra trong ống có chiều dài \(L = 45cm\).

-
A
\(900Hz\)
-
B
\(550Hz\)
-
C
\(180Hz\)
-
D
\(90Hz\)
Đáp án của giáo viên lời giải hay : C
Điều kiện có sóng dừng 1 đầu là nút sóng 1 đầu là bụng sóng: \(l = \left( {2k + 1} \right)\dfrac{\lambda }{4}\)
Bước sóng: \(\lambda = \dfrac{v}{f}\)
Khi khoảng cách giữa piston và đầu hởi của ống là \(L = 45cm\) thì đầu hở của ống nghe thấy âm thanh lớn
\( \Rightarrow \) Đầu piston là nút sóng, đầu hở là bụng sóng.
Ta có hình vẽ minh họa:
Áp dụng điều kiện có sóng dừng một đầu là nút sóng một đầu là bụng sóng ta có:
\(l = \left( {2k + 1} \right)\dfrac{\lambda }{4} = \left( {2k + 1} \right)\dfrac{v}{{4f}} \Rightarrow f = \dfrac{{\left( {2k + 1} \right)v}}{{4.L}}\)
Để \({f_{\min }} \Leftrightarrow {k_{\min }} = 0\) \( \Rightarrow {f_{\min }} = \dfrac{v}{{4.L}} = \dfrac{{330}}{{4.0,45}} = 183,33Hz\)
Sóng dừng truyền trên sợi dây PQ. Biết P, R, Q là nút sóng. S và T là hai điểm trên dây cách R một khoảng x như hình vẽ. Phát biểu nào sau đây đúng về dao động của hai điểm S và T?

-
A
cùng biên độ và cùng pha.
-
B
khác biên độ và cùng pha.
-
C
cùng biên độ và lệch pha 1800.
-
D
khác biên độ và lệch pha 1800.
Đáp án của giáo viên lời giải hay : C
- Hai điểm đối xứng với nhau qua bụng sóng luôn dao động cùng pha
- Hai điểm đối xứng với nhau qua nút sóng luôn dao động ngược pha
- Biên độ dao động của một điểm trên sóng dừng: \({A_M} = 2A\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right|\) với x là khoảng cách từ M tới nút sóng gần nhất.
Nhận xét: hai điểm S, T đối xứng qua nút sóng \( \to \) S, T dao động ngược pha
Khoảng cách từ S và T tới nút sóng gần nhất là R là:
\(RS = RT = x \Rightarrow {A_S} = {A_T}\)
→ Hai điểm S, T dao động cùng biên độ, ngược pha (lệch pha 1800)
