Một dây đàn chiều dài \(\ell \), biết tốc độ truyền sóng ngang theo dây đàn bằng \(v\). Tần số của âm cơ bản (tần số nhỏ nhất) do dây đàn phát ra bằng:
-
A
\(\frac{v}{l}\)
-
B
\(\frac{v}{{2l}}\)
-
C
\(\frac{{2v}}{l}\)
-
D
\(\frac{v}{{4l}}\)
Đáp án của giáo viên lời giải hay : B
Vận dụng biểu thức sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2} = k\frac{v}{{2f}}\)
Ta có điều kiện sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2} = k\frac{v}{{2f}}\)
Ta suy ra: \(f = k\frac{v}{{2l}}\)
Mặt khác, ta có \(k = 1\) ứng với âm cơ bản
=> Tần số của âm cơ bản do dây đàn phát ra bằng: \({f_1} = \frac{v}{{2l}}\)
Tại một điểm trên măt chất lỏng có một nguồn dao động với tần số \(120{\rm{ }}Hz\), tạo ra sóng ổn định trên mặt chất lỏng. Xét \(5\) gợn lồi liên tiếp trên một phương truyền sóng, ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm \(0,5m\). Tốc đô ̣truyền sóng là:
-
A
\(12{\rm{ }}m/s\)
-
B
\(15{\rm{ }}m/s\)
-
C
\(30{\rm{ }}m/s\)
-
D
\(25{\rm{ }}m/s\)
Đáp án của giáo viên lời giải hay : B
+ Khoảng cách giữa \(n\) gợn sóng là \(\left( {n - 1} \right)\lambda \)
+ Sử dụng biểu thức tính tốc độ truyền sóng: \(v = \frac{\lambda }{T} = \lambda f\)
Ta có:
+ Khoảng cách từ gợn sóng thứ nhất đến gợn sóng thứ \(5\) là: \(4\lambda = 0,5m \to \lambda = \frac{{0,5}}{4} = 0,125m\)
+ Tốc độ truyền sóng là: \(v = \lambda f = 0,125.120 = 15m/s\)
Một nguồn âm điểm truyền sóng âm đẳng hướng vào trong không khí với tốc độ truyền âm là \(v\). Khoảng cách giữa \(2\) điểm gần nhau nhất trên cùng phương truyền sóng âm dao động vuông pha nhau là \(d\). Tần số của âm là:
-
A
\(\frac{v}{{2d}}\)
-
B
\(\frac{{2v}}{d}\)
-
C
\(\frac{v}{{4d}}\)
-
D
\(\frac{v}{d}\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức xác định độ lệch pha giữa 2 điểm trên phương truyền sóng: \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
+ Sử dụng biểu thức tính tần số của âm: \(f = \frac{v}{\lambda }\)
+ Khoảng cách giữa hai điểm gần nhau nhất trên cùng hướng truyền sóng dao động vuông pha với nhau nên ta có: \(\Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{\pi }{2} \to \frac{d}{\lambda } = \frac{1}{4} \to \lambda = 4d\) (1)
+ Tần số của âm: \(f = \frac{v}{\lambda }\) (2)
Từ (1) và (2), ta suy ra: \(f = \frac{v}{{4d}}\)
Một lá thép dao động với chu kì \(T = 80ms\). Âm do nó phát ra là:
-
A
Siêu âm
-
B
Hạ âm
-
C
Âm nghe được
-
D
Không phải sóng âm
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức liên hệ giữa chu kì và tần số: \(f = \frac{1}{T}\)
+ Sử dụng giới hạn về các loại âm:
- Âm nghe được: \(16Hz - 20000Hz\)
- Hạ âm: dưới \(16Hz\)
- Siêu âm: trên \(20000Hz\)
Ta có, tần số âm của lá thép là: \(f = \frac{1}{T} = \frac{1}{{{{80.10}^{ - 3}}}} = 12,5Hz < 16Hz\)
=> Âm mà lá thép phát ra là hạ âm
Một cơn động đất phát đồng thời hai sóng cơ trong đất: sóng ngang (N) và sóng dọc (D). Biết rằng vận tốc của sóng (N) là \(34,5km/s\) và của sóng (D) là \(8km/s\). Một máy địa chấn ghi được cả sóng (N) và sóng (D) cho thấy rằng sóng (N) đến sớm hơn sóng (D) là \(4\) phút. Tâm động đất cách máy ghi là:
-
A
\(250km\)
-
B
\(25km\)
-
C
\(5000km\)
-
D
\(2500km\)
Đáp án của giáo viên lời giải hay : D
Vận dụng biểu thức tính quãng đường: \(s = vt\)
Gọi
+ Thời gian máy địa chấn ghi được tín hiệu từ cơn động đất do sóng (N) và sóng (D) truyền đến lần lượt là: \({t_1}\) và \({t_2}\)
+ Khoảng cách từ tâm động đất đến máy địa chấn là: \(s\)
Vận tốc của sóng (N) là: \({v_1} = 34,5km/s\)
Vận tốc của sóng (D) là: \({v_2} = 8km/s\)
Ta có quãng đường truyền của hai sóng là như nhau (đều từ tâm động đất đến máy địa chấn) và bằng \(s\)
Ta suy ra:
\(\left\{ \begin{array}{l}{t_1} = \dfrac{s}{{{v_1}}} = \dfrac{s}{{34,5}}\\{t_2} = \dfrac{s}{{{v_2}}} = \dfrac{s}{{8}}\end{array} \right.\)
Mặt khác, theo đề bài ta có sóng (N) đến sớm hơn sóng (D):
\(4\) phút \( = 4.60 = 240\) giây, ta có:
\(\begin{array}{l}{t_2} - {t_1} = 240\\ \leftrightarrow \dfrac{s}{8} - \dfrac{s}{{34,5}} = 240 \leftrightarrow \dfrac{{53s}}{{552}} = 240\\ \to s = 2499,6km \approx 2500km\end{array}\)
Ba điểm \(O,{\rm{ }}A,{\rm{ }}B\) cùng nằm trên một nửa đường thẳng xuất phát từ \(O\). Tại \(O\) đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm. Mức cường độ âm tại \(A\) là \(50{\rm{ }}dB\), tại \(B\) là \(30{\rm{ }}dB\). Cường độ âm chuẩn \({I_0} = {10^{ - 12}}\left( {W/{m^2}} \right)\) , cường độ âm tại trung điểm $M$ của đoạn $AB$ là:
-
A
\({4,4.10^{ - 9}}{\rm{W}}/{m^2}\)
-
B
\({3,3.10^{ - 9}}{\rm{W}}/{m^2}\)
-
C
\({2,9.10^{ - 9}}{\rm{W}}/{m^2}\)
-
D
\({2,25.10^{ - 9}}{\rm{W}}/{m^2}\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính mức cường độ âm: \(L = 10\log \dfrac{I}{{{I_0}}}\)
+ Sử dụng biểu thức tính hiệu mức cường độ âm: \({L_A} - {L_B} = 10\log \dfrac{{{I_A}}}{{{I_B}}} = 10\log \dfrac{{r_B^2}}{{r_A^2}}\)

Ta có: \({L_A} = 50dB,{L_B} = 30dB\)
Hiệu mức cường độ âm:
\(\begin{array}{l}{L_A} - {L_B} = 10\log \dfrac{{r_B^2}}{{r_A^2}} = 10\log \dfrac{{O{B^2}}}{{O{A^2}}} = 50 - 30 = 20\\ \leftrightarrow \log \dfrac{{O{B^2}}}{{O{A^2}}} = 2 \to O{B^2} = {10^2}O{A^2}\\ \to OB = 10OA\end{array}\)
Ta có: \({r_M} = OM = OB - MB = OB - \dfrac{{(OB - OA)}}{2} = \dfrac{{OB + OA}}{2} = \dfrac{{11OA}}{2}\)
\(\begin{array}{l}{L_A} - {L_M} = 10\log \dfrac{{r_M^2}}{{r_A^2}} = 10\log \dfrac{{{{\left( {\dfrac{{11OA}}{2}} \right)}^2}}}{{O{A^2}}} = 14,8\\ \to {L_M} = 50 - 14,8 = 35,2dB\end{array}\)
Mặt khác, ta có:
\(\begin{array}{l}{L_M} = 10\log \dfrac{{{I_M}}}{{{I_0}}} = 35,2dB\\ \to \log \dfrac{{{I_M}}}{{{I_0}}} = 3,52\\ \to {I_M} = {I_0}{.10^{3,52}} = {10^{ - 12}}{.10^{3,52}} = {3,3.10^{ - 9}}{\rm{W}}/{m^2}\end{array}\)
Một sóng cơ truyền dọc trục Ox theo phương trình \(u = 4\cos \left( {\frac{{\pi t}}{3} + \frac{{\pi x}}{6} - \frac{\pi }{3}} \right)cm\), trong đó x tính bằng m, t tính bằng s. Sóng truyền theo
-
A
Chiều âm của trục Ox với tốc độ \(200cm/s\)
-
B
Chiều dương của trục Ox với tốc độ \(200cm/s\)
-
C
Chiều dương của trục Ox với tốc độ \(2cm/s\)
-
D
Chiều âm của trục Ox với tốc độ \(2cm/s\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng lí thuyết về sự truyền sóng cơ
+ So sánh phương trình với phương trình sóng: \(u = {u_0}{\rm{cos}}\left( {\omega t + \varphi \pm \frac{{2\pi d}}{\lambda }} \right)\)
- Dấu “+” sóng truyền theo chiều âm
- Dấu “-“ sóng truyền theo chiều dương
+ Vận dụng biểu thức xác định tốc độ truyền sóng: \(v = \frac{\lambda }{T} = \lambda f\)
Từ phương trình sóng: \(u = 4\cos \left( {\frac{{\pi t}}{3} + \frac{{\pi x}}{6} - \frac{\pi }{3}} \right)cm\), ta có:
Pha dao động: \(\frac{{\pi t}}{3} - \frac{\pi }{3} + \frac{{\pi x}}{6}\) => Sóng truyền theo chiều âm của trục Ox
\(\frac{{2\pi x}}{\lambda } = \frac{{\pi x}}{6} \to \lambda = 12m\)
Tốc độ truyền sóng: \(v = \frac{\lambda }{T} = \frac{\lambda }{{\frac{{2\pi }}{\omega }}} = \frac{{\lambda \omega }}{{2\pi }} = \frac{{12.\frac{\pi }{3}}}{{2\pi }} = 2m/s = 200cm/s\)
Vậy sóng truyền theo chiều âm của trục Ox với tốc độ \(200cm/s\)
Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp được đặt tại A và B dao động theo phương trình \({u_A} = {u_B} = a\cos 25\pi t\) ( \(a\) không đổi, \(t\) tính bằng \(s\) ). Trên đoạn thẳng AB, hai điểm có phần tử nước dao động với biên độ cực đại cách nhau một khoảng ngắn nhất là \(2cm\). Tốc độ truyền sóng là:
-
A
\(25cm/s\)
-
B
\(100cm/s\)
-
C
\(75cm/s\)
-
D
\(50cm/s\)
Đáp án của giáo viên lời giải hay : D
+ Khoảng cách giữa hai điểm gần nhất trên phương truyền sóng dao động với biên độ cực đại là: \(\frac{\lambda }{2}\)
+ Sử dụng biểu thức tính tốc độ truyền sóng: \(v = \frac{\lambda }{T} = \lambda f\)
Ta có:
+ Khoảng cách giữa hai điểm dao động với biên độ cực đại cách nhau một khoảng ngắn nhất là: \(\frac{\lambda }{2} = 2cm \to \lambda = 4cm\)
+ Tốc độ truyền sóng: \(v = \frac{\lambda }{T} = \frac{\lambda }{{\frac{{2\pi }}{\omega }}} = \frac{4}{{\frac{{2\pi }}{{25\pi }}}} = 50cm/s\)
Một sóng cơ hình sin truyền theo trục Ox với chu kì T. Khoảng thời gian để sóng truyền được quãng đường bằng một bước sóng là:
-
A
4T
-
B
0,5T
-
C
T
-
D
2T
Đáp án của giáo viên lời giải hay : C
Khoảng thời gian để sóng truyền được quãng đường bằng một bước sóng là một chu kỳ
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm $A$ và $B$ dao động cùng pha theo phương thẳng đứng. Trên đoạn thẳng $AB$, khoảng cách giữa hai cực tiểu giao thoa liên tiếp là $0,5 cm$. Sóng truyền trên mặt nước có bước sóng là:
-
A
1,0 cm
-
B
2,0 cm
-
C
4,0 cm
-
D
0,25 cm
Đáp án của giáo viên lời giải hay : A
Khoảng cách giữa hai cực đại giao thoa (hoặc cực tiểu giao thoa) là \(\dfrac{\lambda }{2}\)
Ta có khoảng cách giữa hai cực tiểu giao thoa liên tiếp là \(\dfrac{\lambda }{2} = 0,5cm\)
=> sóng truyền trên mặt nước có bước sóng là \(\lambda = 0,5.2 = 1cm\)
Một sóng cơ có tần số \(f{\rm{ }} = {\rm{ }}5Hz\), truyền dọc theo sợi dây đàn hồi với tốc độ truyền sóng \(v{\rm{ }} = {\rm{ }}5m/s\). Bước sóng là:
-
A
\(1m\)
-
B
\(0,318m\)
-
C
\(0,318m\)
-
D
\(3,14m\)
Đáp án của giáo viên lời giải hay : A
Áp dụng công thức tính bước sóng \(\lambda = \frac{v}{f}\)
Ta có, bước sóng \(\lambda = \frac{v}{f} = \frac{5}{5} = 1m\)
Cường độ âm tại một điểm trong môi trường truyền âm là \({10^{ - 5}}W/{m^2}\). Biết cường độ âm chuẩn là \({10^{ - 12}}W/{m^2}\). Mức cường độ âm tại điểm đó bằng:
-
A
\(70B\)
-
B
\(0,7B\)
-
C
\(0,7dB\)
-
D
\(70dB\)
Đáp án của giáo viên lời giải hay : D
Áp dụng công thức tính mức cường độ âm: \(L = 10\log \frac{I}{{{I_0}}}\)
Ta có, mức cường độ âm: \(L = \log \frac{I}{{{I_0}}} = \log \frac{{{{10}^{ - 5}}}}{{{{10}^{ - 12}}}} = 7B = 70dB\)
Sóng dừng trên dây \(AB\) có chiều dài \(32cm\) với hai đầu cố định. Tần số dao động của dây là \(50Hz\), tốc độ truyền sóng trên dây là \(4m/s\). Trên dây có:
-
A
\(5\) nút sóng, \(4\) bụng sóng
-
B
\(4\) nút sóng, \(4\) bụng sóng
-
C
\(9\) nút sóng, \(8\) bụng sóng
-
D
8 nút sóng, \(8\) bụng sóng
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \frac{v}{f}\)
+ Sử dụng lí thuyết về điều kiện có sóng dừng trên dây hai đầu cố định \(l = n\frac{\lambda }{2}\) (n – số bụng sóng)
- Số bụng sóng: \(n\)
- Số nút sóng: \(n + 1\)
Ta có:
+ Bước sóng: \(\lambda = \frac{v}{f} = \frac{4}{{50}} = 0,08m = 8cm\)
+ Mặt khác, ta có dây hai đầu cố định => chiều dài dây: \(l = n\frac{\lambda }{2}\)
Thay vào ta được: \(32 = n\frac{8}{2} \to n = 8\)
=> Trên dây có 8 bụng và 9 nút
Một sóng cơ học truyền dọc theo trục Ox có phương trình \(u = Acos\left( {20\pi t-\pi x} \right){\rm{ }}\left( {cm} \right)\) , với t tính bằng giây. Tần số của sóng này bằng:
-
A
\(20Hz\)
-
B
\(5Hz\)
-
C
\(15Hz\)
-
D
\(10Hz\)
Đáp án của giáo viên lời giải hay : D
+ Đọc phương trình sóng
+ Áp dụng công thức tính tần số: \(f = \frac{\omega }{{2\pi }}\)
Từ phương trình sóng: \(u = Acos\left( {20\pi t--\pi x} \right){\rm{ }}\left( {cm} \right)\)
Ta suy ra, tần số góc \(\omega = 20\pi \)
\( \to f = \frac{\omega }{{2\pi }} = 10Hz\)
Ở mặt nước có hai nguồn kết hợp \(A,{\rm{ }}B\) dao động theo phương thẳng đứng với phương trình \({u_A} = {\rm{ }}{u_B} = {\rm{ }}4cos\left( {\omega t} \right){\rm{ }}\left( {mm} \right)\). Tốc độ truyền sóng và biên độ sóng không đổi khi sóng truyền đi. Phần tử \(M\) ở mặt nước thuộc vân giao thoa cực tiểu có biên độ dao động là:
-
A
\(4cm\)
-
B
\(0mm\)
-
C
\(4mm\)
-
D
\(8mm\)
Đáp án của giáo viên lời giải hay : B
Những điểm thuộc vân giao thoa cực tiểu có biên độ dao động bằng 0
Ở mặt nước, một nguồn sóng đặt tại \(O\) dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước với bước sóng \(\lambda \). \(M\) và \(N\) là hai điểm ở mặt nước sao cho \(OM = 6\lambda ,ON = 8\lambda \) và \(OM\) vuông góc với \(ON\). Trên đoạn thẳng \(MN\), số điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn \(O\) là:
-
A
3
-
B
6
-
C
5
-
D
4
Đáp án của giáo viên lời giải hay : D
+ Sử dụng hệ thức lượng trong tam giác vuông
+ Sử dụng điều kiện dao động ngược pha: \(d = \left( {k + \frac{1}{2}} \right)\lambda \)
\(OH\) là đường cao hạ từ \(O\) xuống
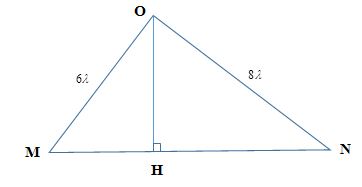
+ Ta có:
\(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} = \dfrac{1}{{{6^2}}} + \dfrac{1}{{{8^2}}} = \dfrac{{25}}{{576}}\\ \to OH = 4,8\lambda \end{array}\)
+ Các điểm trên \(MN\) ngược pha với nguồn thỏa mãn \(d = (k + 0,5)\lambda \) ta xác định được
- Trong khoảng \(HM\), ta có:
\(\begin{array}{l}OH \le d \le OM\\ \Leftrightarrow 4,8\lambda \le \left( {k + 0,5} \right)\lambda \le 6\lambda \\ \Leftrightarrow 4,3 \le k \le 5,5\end{array}\)
=> có \(1\) điểm ứng với \(k = 5\)
- Trong khoảng \(HN\), ta có:
\(\begin{array}{l}OH \le d \le ON\\ \Leftrightarrow 4,8\lambda \le \left( {k + 0,5} \right)\lambda \le 8\lambda \\ \Leftrightarrow 4,3 \le k \le 7,5\end{array}\)
=> có \(3\) điểm ứng với \(k = 5,6,7\)
Vậy trên đoạn thẳng \(MN\), có 4 điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn \(O\)
Sóng cơ truyền được trong các môi trường:
-
A
khí, chân không và rắn.
-
B
lỏng, khí và chân không.
-
C
chân không, rắn và lỏng.
-
D
rắn, lỏng và khí
Đáp án của giáo viên lời giải hay : D
Sóng cơ chỉ truyền được trong các môi trường rắn , lỏng, khí
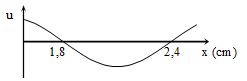
Một sóng hình sin truyền trên một sợi dây dài.Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng :
-
A
\(1,2cm\)
-
B
\(0,6cm\)
-
C
\(2,4cm\)
-
D
\(0,3cm\)
Đáp án của giáo viên lời giải hay : A
Khoảng cách giữa hai nút sóng liên tiếp trên cùng một phương truyền sóng là \(\frac{\lambda }{2}\)
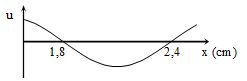
Từ đồ thị, ta thấy, khoảng cách giữa hai nút liên tiếp là một nửa bước sóng
=> \(2,4 - 1,8 = \frac{\lambda }{2} = 0,6 \to \lambda = 1,2cm\)
Ở mặt nước có hai nguồn kết hợp đặt tại hai điểm \(A\) và \(B\), dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng \(\lambda \). Trên \(AB\) có \(9\) vị trí mà ở đó các phần tử nước dao động với biên độ cực đại. \(C\) và \(D\) là hai điểm ở mặt nước sao cho \(ABCD\) là hình vuông. \(M\) là một điểm thuộc cạnh \(CD\) và nằm trên vân cực đại giao thoa bậc nhất \(\left( {MA - MB = \lambda } \right)\). Biết phần tử tại \(M\) dao động ngược pha với các nguồn. Độ dài đoạn \(AB\) gần nhất với giá trị nào sau đây?
-
A
\(4,6\lambda \)
-
B
\(4,4\lambda \)
-
C
\(4,7\lambda \)
-
D
\(4,3\lambda \)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng điều kiện cực đại giao thoa của hai nguồn cùng pha: \({d_1} - {d_2} = k\lambda \)
+ Sử dụng điều kiện dao động ngược pha với nguồn: \({d_1} - {d_2} = \left( {2k + 1} \right)\lambda \)
\(M\) là cực đại giao thoa và ngược pha với hai nguồn, ta có:
+ Điều kiện cực đại giao thoa của hai nguồn cùng pha: \({d_1} - {d_2} = k\lambda \)
+ Điều kiện dao động ngược pha với nguồn: \({d_1} - {d_2} = \left( {2k + 1} \right)\lambda \)
=> \(\left\{ \begin{array}{l}{d_1} - {d_2} = n\lambda \\{d_1} + {d_2} = m\lambda \end{array} \right.(1)\) n và m là số nguyên n lẻ, m chẵn
Theo đề bài ta có : \({d_1} - {d_2} = MA - MB = \lambda \)
Vì \(n{\rm{ }} = {\rm{ }}1\)
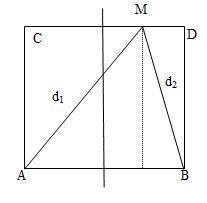
Trên hình, theo đề ta có :\(\left\{ \begin{array}{l}{d_1} + {d_2} > 2AB\\4\lambda \le AB < 5\lambda \end{array} \right.\left( 2 \right)\)
Từ (1) và (2) => \(\left\{ \begin{array}{l}{d_1} - {d_2} = \lambda \\{d_1} + {d_2} = 10\lambda \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{d_1} = 5,5\lambda \\{d_2} = 4,5\lambda \end{array} \right..\)
\(\sqrt {{{5,5}^2}{\lambda ^2} - A{B^2}} + \sqrt {{{4,5}^2}\lambda - A{B^2}} = AB \to AB = 4,376749\lambda \)
Tần số của âm cơ bản và họa âm do một dây đàn phát ra tương ứng bằng với tần số của sóng cơ để trên dây đàn có sóng dừng. Trong các họa âm do dây đàn phát ra, có hai họa âm ứng với tần số \(2640{\rm{ }}Hz\) và \(4400{\rm{ }}Hz\). Biết âm cơ bản của dây đàn có tần số nằm trong khoảng từ \(300{\rm{ }}Hz\) đến \(800{\rm{ }}Hz\). Trong vùng tần số của âm nghe được từ \(16{\rm{ }}Hz\) đến \(20{\rm{ }}kHz\), có tối đa bao nhiêu tần số của họa âm (kể cả âm cơ bản) của dây đàn này?
-
A
37
-
B
30
-
C
45
-
D
22
Đáp án của giáo viên lời giải hay : C
+ Áp dụng lý thuyết âm sắc
+ Họa âm: \({f_n} = n{f_1}\) với \({f_1}\) - tần số âm cơ bản
Gọi \({f_1}\) là tần số âm cơ bản
=> \(2640Hz\) và \(4400Hz\) phải chia hết cho \({f_1}\)
=> \({f_1}\) là ước chung của \(2640\) và \(4400\)
Ta có, ước chung lớn nhất của \(2640\) và \(4400\) là \(880\)
=> \({f_1}\) là ước của \(880\)
Lại có \(300 < {f_1} < 800\)
Từ đó, ta suy ra : \({f_1} = 440Hz\)
Họa âm của âm : \({f_n} = n{f_1}\)
Trong vùng tần số của âm nghe được \(16Hz - 20000Hz\),
\(\begin{array}{l}16 < 440n < 20000\\ \leftrightarrow 0,036 < n < 45,45\\ \to n = 1,2,...,45\end{array}\)
=> Có 45 họa âm kể cả âm cơ bản
Ở mặt nước, tại hai điểm \({S_1}\) và \({S_2}\) có hai nguồn dao động cùng pha theo phương thẳng đứng, phát ra hai sóng kết hợp có bước sóng \(\lambda \). Cho \({S_1}{S_2} = {\rm{ }}5,4\lambda \). Gọi (C) là hình tròn nằm ở mặt nước có đường kính là \({S_1}{S_2}\). Số vị trí trong (C) mà các phần tử ở đó dao động với biên độ cực đại và cùng pha với dao động của các nguồn là :
-
A
18
-
B
9
-
C
22
-
D
11
Đáp án của giáo viên lời giải hay : A
+ Sử dụng điều kiện dao động cực đại trong giao thoa của hai nguồn cùng pha : \({d_2} - {d_1} = k\lambda \)
+ Sử dụng định lí hàm số cos trong tam giác
Điều kiện để điểm dao động với biên độ cực đại trong giao thoa hai nguồn cùng pha là \({d_2} - {d_1} = k\lambda \)
- Áp dụng định lí hàm cos trong tam giác
Gọi M là một điểm bất kỳ trên nửa phía trên.
- Để tại M các phần tử nước dao động với biên độ cực đại và cùng pha với nguồn thì sóng do hai nguồn truyền tới M phải cùng pha với nhau và cùng pha với nguồn, suy ra M phải cách các nguồn một số nguyên lần bước sóng
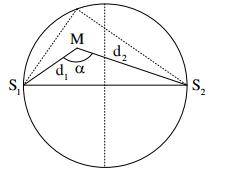
\(\left\{ \begin{array}{l}{d_1} = {k_1}\lambda \\{d_2} = {k_2}\lambda \end{array} \right.\)
Để M nằm bên trong đường tròn (C) thì \(\alpha > {90^0} = > \cos \alpha < 0\)
Áp dụng định lý hàm cos cho tam giác MS1S2 ta có :
\(\begin{array}{l}\cos \alpha = \frac{{d_1^2 + d_2^2 - {{\left( {{S_1}{S_2}} \right)}^2}}}{{2{d_1}{d_2}}} = \frac{{k_1^2 + k_2^2 - {{5,4}^2}}}{{2{k_1}{k_2}}}\\\cos \alpha < 0 = > k_1^2 + k_2^2 < {5,4^2} = 29,16\\ = > \left| {{d_1} - {d_2}} \right| < {S_1}{S_2} < {d_1} + {d_2} = > \left| {{k_1} - {k_2}} \right| < 5,4 \le {k_1} + {k_2}\end{array}\)
Vậy có tất cả 9 điểm
=> Tính thêm nửa dưới ta có 18 điểm
Trên mặt một chất lỏng có hai nguồn sóng kết hợp cùng pha có biên độ \(1,5A\) và \(2A\) dao động vuông góc với mặt thoáng chất lỏng. Nếu cho rằng sóng truyền đi với biên độ không thay đổi thì tại một điểm $M$ cách hai nguồn những khoảng $d_1 = 5,75λ$ và $d_2 = 9,75λ$ sẽ có biên độ dao động:
-
A
$A_M = 3,5A$
-
B
\({A_M} = \sqrt {6,25} A\)
-
C
$A_M = 3A$
-
D
$A_M = 2A$
Đáp án của giáo viên lời giải hay : A
+ Viết phương trình sóng tại M do mỗi nguồn truyền đến
+ Sử dụng công thức tổng hợp biên độ: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}cos\Delta \varphi \)
Sóng tại \(M\) nhận được do mỗi nguồn truyền đến:
\(\begin{array}{l}{u_{1M}} = 1,5{\rm{A}}c{\rm{os}}(\varphi - \dfrac{{2\pi {{\rm{d}}_1}}}{\lambda })\\ = 1,5{\rm{A}}c{\rm{os}}(\varphi - 11,5\pi )\\{u_{2M}} = 2{\rm{A}}c{\rm{os}}(\varphi - \dfrac{{2\pi {{\rm{d}}_2}}}{\lambda })\\ = 2{\rm{A}}c{\rm{os}}(\varphi - 19,5\pi )\end{array}\)
Sóng tổng hợp tại M có biên độ:
\(\begin{array}{l}{{\rm{A}}_M} = \sqrt {A_1^2 + A_2^2 + 2{{\rm{A}}_1}{A_2}{\rm{cos}}\Delta \varphi } \\ = \sqrt {{{\left( {1,5A} \right)}^2} + {{\left( {2A} \right)}^2} + 2.1,5A.2A.cos\left( { - 19,5\pi - \left( { - 11,5\pi } \right)} \right)} \\ = 3,5{\rm{A}}\end{array}\)
Một sóng cơ truyền trong môi trường đồng chất dọc theo trục \(Ox\) có phương trình dao động \(u = 8cos\left( {2000\pi t - 20\pi x + \frac{\pi }{4}} \right)mm\), trong đó \(x\) tính bằng \(cm\), \(t\) tính bằng \(s\). Vào thời điểm \(t{\rm{ }} = {\rm{ }}0,0125s\), sóng truyền qua vị trí \(x{\rm{ }} = {\rm{ }}4,5cm\) với tốc độ truyền sóng \(v\). Giá trị của \(v\) bằng:
-
A
\(100cm/s\)
-
B
\(4,44cm/s\)
-
C
\(444mm/s\)
-
D
\(100mm/s\)
Đáp án của giáo viên lời giải hay : A
+ Đọc phương trình sóng
+ Sử dụng biểu thức \(\frac{{2\pi x}}{\lambda }\)
+ Sử dụng công thức tính bước sóng \(\lambda = v.T = \frac{v}{f}\)
Từ phương trình sóng, ta có:
+ \(\omega = 2000\pi \to f = \frac{\omega }{{2\pi }} = \frac{{2000\pi }}{{2\pi }} = 1000Hz\)
+ Mặt khác, \(20\pi x = \frac{{2\pi x}}{\lambda } \to \lambda = \frac{{2\pi }}{{20\pi }} = 0,1cm\)
=> Vận tốc truyền sóng: \(v = \lambda f = 0,1.1000 = 100cm/s\)
Một người đứng cách nguồn âm \(S\) một đoạn \(d\). Nguồn này phát sóng cầu. Khi người đó đi lại gần nguồn âm \(50m\) thì thấy mức cường độ âm tăng thêm \(3dB\). Khoảng cách \(d\) là :
-
A
\(22,5m\)
-
B
\(29,3m\)
-
C
\(222m\)
-
D
\(171m\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng công thức tính cường độ âm \(I = \frac{P}{{4\pi {d^2}}}\)
+ Sử dụng công thức tính mức cường độ âm \(L = 10lg\frac{I}{{{I_0}}}(dB)\)
+ Vận dụng biểu thức tính hiệu mức cường độ âm: \({L_2} - {L_1} = 10\log \frac{{{I_2}}}{{{I_1}}} = 10\log \frac{{r_1^2}}{{r_2^2}}\)
Ta có:
\(\begin{array}{l}{I_1} = \frac{P}{{4\pi {d^2}}} \Rightarrow {L_1} = 10lg\frac{{{I_1}}}{{{I_0}}}(dB);(1)\\{I_2} = \frac{P}{{4\pi {{(d - 50)}^2}}} \Rightarrow {L_2} = 10lg\frac{{{I_2}}}{{{I_0}}}(dB);(2)\end{array}\)
Khi người đó đi lại gần nguồn âm \(50m\) thì thấy mức cường độ âm tăng thêm \(3dB\)
Ta có:
\(\begin{array}{l}{L_2} - {L_1} = 3dB\\ \leftrightarrow 10\log \frac{{r_1^2}}{{r_2^2}} = 3\\ \leftrightarrow 10\log \frac{{{d^2}}}{{{{\left( {d - 50} \right)}^2}}} = 3\\ \to \frac{{{d^2}}}{{{{\left( {d - 50} \right)}^2}}} = {10^{\frac{3}{{10}}}} \to d \approx 171,2m\end{array}\)
Hai điểm \(A\) và \(B\) trên mặt nước cách nhau \(12cm\) phát ra hai sóng kết hợp có phương trình: \({u_1} = {u_2} = acos40\pi t\left( {cm} \right)\),tốc độ truyền sóng trên mặt nước là \(30cm/s\). Xét đoạn thẳng \(CD{\rm{ }} = {\rm{ }}6cm\) trên mặt nước có chung đường trung trực với \(AB\). Khoảng cách lớn nhất từ \(CD\) đến \(AB\) sao cho trên đoạn \(CD\) chỉ có \(5\) điểm dao động với biên độ cực đại là
-
A
\(10,06cm\)
-
B
\(4,5cm\)
-
C
\(9,25cm\)
-
D
\(6,78cm\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính tần số: \(f = \frac{\omega }{{2\pi }}\)
+ Sử dụng lí thuyết về giao thoa hai nguồn cùng pha
+ Sử dụng điều kiện để điểm dao động với biên độ cực đại trong giao thoa hai nguồn cùng pha là \({d_2} - {d_1} = k\lambda \)
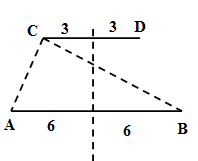
Ta có:
+ Tần số của sóng : \(f = \frac{\omega }{{2\pi }} = \frac{{40\pi }}{{2\pi }} = 20Hz\)
+ Bước sóng : \(\lambda = \frac{v}{f} = \frac{{30}}{{20}} = 1,5cm\)
Để trên \(CD\) xa \(AB\) nhất mà trên đoạn \(CD\) chỉ có \(5\) điểm dao động cực đại thì \(C\) và \(D\) nằm trên các đường cực đại bậc \(2\)
\(\begin{array}{l}CA - CB = - 2\lambda \\ \Leftrightarrow \sqrt {{d^2} + {3^2}} - \sqrt {{d^2} + {9^2}} = - 2.1,5\\ \to d = 10,06cm\end{array}\)
Một sợi dây bằng sắt, mảnh, dài \(120{\rm{ }}cm\) căng ngang, có hai đầu cố định. Ở phía trên, gần sợi dây có một nam châm điện được nuôi bằng nguồn điện xoay chiều có tần số \(50{\rm{ }}Hz\). Trên dây xuất hiện sóng dừng với \(2\) bụng sóng. Tốc độ truyền sóng trên dây là:
-
A
\(120{\rm{ }}m/s\)
-
B
\(60{\rm{ }}m/s\)
-
C
\(180{\rm{ }}m/s\)
-
D
\(240{\rm{ }}m/s\)
Đáp án của giáo viên lời giải hay : A
+ Áp dụng điều kiện có sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2}\)
+ Sử dụng biểu thức tính tốc độ truyền sóng: \(v = \lambda f\)
Ta có sóng dừng trên dây hai đầu cố định nên \(l = k\dfrac{\lambda }{2}\)
+ Theo đề bài, trên dây xuất hiện sóng dừng với hai bụng sóng => \(k = 2\)
Thay \(\left\{ \begin{array}{l}k = 2\\l = 120cm = 1,2m\end{array} \right.\) vào ta được \(1,2 = 2\dfrac{\lambda }{2} \to \lambda = 1,2m\)
+ Tần số dao động của dây \(f_d=2f=2.50=100Hz\)
=> Tốc độ truyền sóng trên dây: \(v = \lambda f_d = 1,2.100 = 120m/s\)
Một sóng ngang truyền trên sợi dây đàn hồi rất dài với vận tốc sóng \(v{\rm{ }} = {\rm{ }}0,2{\rm{ }}m/s\), chu kì dao động \(T = 10s\). Khoảng cách giữa hai điểm gần nhau nhất trên dây dao động ngược pha nhau là:
-
A
\(2{\rm{ }}m\)
-
B
\(1{\rm{ }}m\)
-
C
\(1,5{\rm{ }}m\)
-
D
\(0,5{\rm{ }}m\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính bước sóng: \(\lambda = vT\)
+ Khoảng cách giữa 2 điểm gần nhau nhất dao động ngược pha trên cùng một phương truyền sóng là \(\dfrac{\lambda }{2}\)
+ Bước sóng \(\lambda = vT = 0,2.10{\rm{ }} = 2m\)
+ Khoảng cách giữa 2 điểm gần nhau nhất dao động ngược pha là \(\dfrac{\lambda }{2} = \dfrac{2}{2} = 1m\)
Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số \(120{\rm{ }}Hz\), tạo ra sóng ổn định trên mặt chất lỏng. Xét \(5\) gợn lồi liên tiếp trên một phương truyền sóng, ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm \(0,5{\rm{ }}m\). Tốc độ truyền sóng là:
-
A
\(12{\rm{ }}m/s\)
-
B
\(30{\rm{ }}m/s\)
-
C
\(25{\rm{ }}m/s\)
-
D
\(15{\rm{ }}m/s\)
Đáp án của giáo viên lời giải hay : D
+ Khoảng cách giữa n gợn lồi liên tiếp là \(\left( {n - 1} \right)\lambda \)
+ Sử dụng biểu thức tính tốc độ truyền sóng: \(v = \lambda .f\)
+ Khoảng cách giữa \(5\) gợn lồi liên tiếp là: \(4\lambda = 0,5m \to \lambda = \frac{{0,5}}{4} = 0,125m\)
+ Tốc độ truyền sóng: \(v = \lambda f = 0,125.120 = 15m/s\)
Tại điểm \(S\) trên mặt nước yên tĩnh có nguồn dao động điều hoà theo phương thẳng đứng với tần số \(50Hz\). Khi đó trên mặt nước hình thành hệ sóng tròn đồng tâm \(S\). Tại hai điểm \(M,{\rm{ }}N\) nằm cách nhau \(9cm\) trên đường thẳng đi qua \(S\) luôn dao động cùng pha với nhau. Biết rằng, tốc độ truyền sóng thay đổi trong khoảng từ \(70cm/s\) đến \(80cm/s\). Tốc độ truyền sóng trên mặt nước là:
-
A
\(75cm/s\)
-
B
\(80cm/s\)
-
C
\(70cm/s\)
-
D
\(72cm/s\)
Đáp án của giáo viên lời giải hay : A
Áp dụng công thức tính độ pha giữa hai điểm trên phương truyền sóng\(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
Tại M, N luôn dao đông cùng pha:
\(\begin{array}{l}\Delta \varphi = \frac{{2\pi .9}}{\lambda } = \frac{{18\pi }}{\lambda } = \frac{{18\pi f}}{v} = 2k\pi \\ \Rightarrow 70cm/s \le v = \frac{{18\pi f}}{{2k\pi }} = \frac{{9f}}{k} \le 80cm/s\\ \Rightarrow 5,6 \le k \le 6,4\\ \Rightarrow k = 6 \Rightarrow v = 75cm/s\end{array}\)
Tại hai điểm \(A\) và \(B\) ở mặt chất lỏng có \(2\) nguồn kết hợp dao động điều hòa theo phương thẳng đứng và cùng pha. \(Ax\) là nửa đường thẳng nằm ở mặt chất lỏng và vuông góc với \(AB\). Trên \(Ax\) có những điểm mà các phần tử ở đó dao động với biên độ cực đại, trong đó \(M\) là điểm xa \(A\) nhất, \(N\) là điểm kế tiếp với \(M\), \(P\) là điểm kế tiếp với \(N\) và \(Q\) là điểm gần \(A\) nhất. Biết \(MN{\rm{ }} = {\rm{ }}22,25{\rm{ }}cm\) và \(NP{\rm{ }} = {\rm{ }}8,75{\rm{ }}cm\). Độ dài đoạn \(QA\) gần nhất với giá trị nào sau đây?
-
A
\(1,2{\rm{ }}cm\)
-
B
\(3,1{\rm{ }}cm\)
-
C
\(4,2{\rm{ }}cm\)
-
D
\(2,1{\rm{ }}cm\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng lí thuyết về giao thoa hai nguồn cùng pha.
+ Sử dụng điều kiện để điểm dao động với biên độ cực đại trong giao thoa hai nguồn cùng pha là : \({d_2} - {d_1} = k\lambda \)
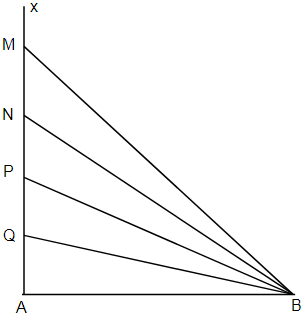
+ Ta thấy trên nửa đường thẳng kẻ từ \(A\) vuông góc với \(AB\) có \(4\) điểm theo thứ tự \(M,N,P,Q\) dao động với biên độ cực đại
=> Nên \(AB\) có \(9\) điểm dao động với biên độ cực đại với: \( - 4 \le k \le 4\left( {{d_2} - {d_1} = k\lambda } \right)\)
Cực đại $M,N,P,Q$ ứng với $k = 1,2,3,4$
+ Đặt $AB = a$
Tại $C$ trên \(Ax\) là điểm dao động với biên độ cực đại:
\(CB - CA = k\lambda \left( * \right)\)
\(\begin{array}{l}C{B^2} - C{A^2} = {a^2}\\ \to \left( {CB - CA} \right)\left( {CB + CA} \right) = {a^2}\\ \to CB + CA = \dfrac{{{a^2}}}{{k\lambda }}\left( {**} \right)\end{array}\)
Từ \(\left( * \right)\) và \(\left( {**} \right)\) ta suy ra: \(CA = \dfrac{{{a^2}}}{{2k\lambda }} - \dfrac{{k\lambda }}{2}\)
- Tại \(M\) ứng với \(k = 1\): \(MA = \dfrac{{{a^2}}}{{2\lambda }} - \dfrac{\lambda }{2}\left( 1 \right)\)
- Tại \(N\) ứng với \(k = 2\): \(NA = \dfrac{{{a^2}}}{{2.2\lambda }} - \dfrac{{2\lambda }}{2} = \dfrac{{{a^2}}}{{4\lambda }} - \lambda \left( 2 \right)\)
- Tại \(P\) ứng với \(k = 3\): \(PA = \dfrac{{{a^2}}}{{2.3\lambda }} - \dfrac{{3\lambda }}{2} = \dfrac{{{a^2}}}{{6\lambda }} - \dfrac{{3\lambda }}{2}\left( 3 \right)\)
- Tại \(Q\) ứng với \(k = 4\): \(QA = \dfrac{{{a^2}}}{{2.4\lambda }} - \dfrac{{4\lambda }}{2} = \dfrac{{{a^2}}}{{8\lambda }} - 2\lambda \left( 4 \right)\)
Lấy \(\left( 1 \right) - \left( 2 \right)\) ta được: \(MN = MA - NA = \dfrac{{{a^2}}}{{4\lambda }} + \dfrac{\lambda }{2} = 22,25cm\left( 5 \right)\)
Lấy \(\left( 2 \right) - \left( 3 \right)\) ta được: \(NP = NA - PA = \dfrac{{{a^2}}}{{12\lambda }} + \dfrac{\lambda }{2} = 8,75cm\left( 6 \right)\)
Lấy \(3.\left( 6 \right) - \left( 5 \right)\) ta được:
\(\begin{array}{l}3\left( {\dfrac{{{a^2}}}{{12\lambda }} + \dfrac{\lambda }{2}} \right) - \left( {\dfrac{{{a^2}}}{4} + \dfrac{\lambda }{2}} \right) = 3.8,75 - 22,25\\ \to \lambda = 4cm\end{array}\)
Lấy \(\left( 5 \right) - \left( 6 \right)\) ta được: \(\dfrac{{{a^2}}}{{6\lambda }} = 22,25 - 8,75 = 13,5cm \to \dfrac{{{a^2}}}{\lambda } = 81cm\)
Thay \(\left\{ \begin{array}{l}\lambda = 4cm\\\dfrac{{{a^2}}}{\lambda } = 81cm\end{array} \right.\) vào \(\left( 4 \right)\) ta được: \(QA = \dfrac{{{a^2}}}{{8\lambda }} - 2\lambda = \dfrac{{81}}{8} - 2.4 = 2,125cm\)
Ở mặt nước, một nguồn sóng đặt tại O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước với bước sóng \(\lambda \). M và N là hai điểm ở mặt nước sao cho \(OM{\rm{ }} = {\rm{ }}6\lambda \), \(ON{\rm{ }} = {\rm{ }}8\lambda \) và OM vuông góc với ON. Trên đoạn thẳng MN, số điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn O là:
-
A
3.
-
B
6.
-
C
5.
-
D
4.
Đáp án của giáo viên lời giải hay : D
Sử dụng điều kiện ngược pha: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \left( {2k + 1} \right)\pi \)
OH là đường cao hạ từ O xuống MN, \(OH = 4,8\lambda \);
Các điểm trên MN ngược pha với nguồn thỏa mãn \(d = (k + 0,5)\lambda \)
Ta xác định được trong khoảng HM \(4,2 \le k \le 5,5\) có 1 điểm ứng với \(k = 5\)
Trong khoảng HN \(4,2 \le k \le 7,5\) có 3 điểm ứng với \(k = 5,6,7\).
=> Trên đoạn thẳng MN, số điểm mà tại đó các phần tử nước dao động ngược pha với dao động của nguồn O là 4 điểm
Ở mặt nước, một nguồn sóng đặt tại điểm O dao động điều hòa theo phương thẳng đứng. Sóng truyền trên mặt nước có bước sóng \(5 cm\). M và N là hai điểm trên mặt nước mà phần tử nước ở đó dao động cùng pha với nguồn. Trên các đoạn OM, ON và MN có số điểm mà phần tử nước ở đó dao động ngược pha với nguồn lần lượt là \(5\), \(3\) và \(3\). Độ dài đoạn MN có giá trị gần nhất với giá trị nào sau đây?
-
A
\(40 cm\).
-
B
\(20 cm\).
-
C
\(30 cm\).
-
D
\(10 cm\).
Đáp án của giáo viên lời giải hay : C
+ Vận dụng tính chất cùng pha, ngược pha của các điểm
+ Sử dụng hệ thức lượng trong tam giác
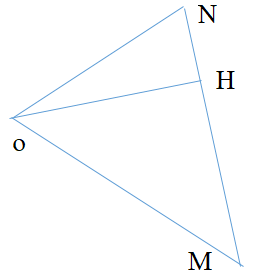
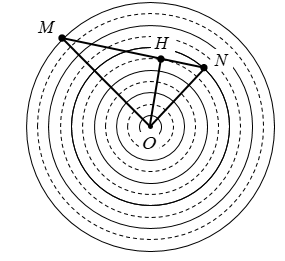
Để dễ hình dung, ta biểu diễn các vị trí dao động cùng pha với nguồn tại cùng một thời điểm bằng các đường nét liền, các điểm dao động ngược pha với nguồn bằng các đường nét đứt.
Trên OM có 5 điểm ngược pha, M là cực đại nên \(OM = 5\lambda = 25cm\)
Tương tự, ta có \(ON = 15 cm\)
Để trên MN có 3 cực đại thì H phải là chân của đường cao kẻ từ điểm , mặc khác
có \(OH = 2,5\lambda = 12,5cm\)
\(MN = MH + NH = \sqrt {{{25}^2} - 12,{5^2}} + \sqrt {{{15}^2} - 12,{5^2}} = 29,9cm\)
Ở mặt thoáng của một chất lỏng có hai nguồn sóng A, B dao động theo phương thẳng đứng với phương trình lần lượt là \({u_A} = a.\cos \omega t\) và \({u_B} = 2a.\cos \omega t\). Bước sóng trên mặt chất lỏng là λ. Coi biên độ sóng không đổi khi truyền đi. Điểm M ở mặt chất lỏng không nằm trên đường AB, cách các nguồn A, B những đoạn lần lượt là 18,25λ và 9,75λ. Biên độ dao động của điểm M là:
-
A
2a
-
B
a
-
C
3a
-
D
\(a\sqrt 5 \)
Đáp án của giáo viên lời giải hay : B
Phương trình sóng tại M do nguồn A truyền đến:
\({u_{AM}} = a.\cos \left[ {\omega .\left( {t - \frac{{{d_1}}}{v}} \right)} \right]\)
Phương trình sóng tại M do B truyền đến:
\({u_{BM}} = 2a.\cos \left[ {\omega .\left( {t - \frac{{{d_2}}}{v}} \right)} \right]\)
Phương trình sóng tại M là tổng hợp của hai sóng truyền tới, thực hiện tổng hợp bằng phương pháp tổng hợp fresnel.
Biên độ dao động của phần tử tại M là:
\(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \left( {\Delta \varphi } \right)} \)
Phương trình sóng tại M do nguồn A và B truyền đến lần lượt là:
\(\left\{ \begin{array}{l}
{u_{AM}} = a.\cos \left[ {\omega .\left( {t - \frac{{{d_1}}}{v}} \right)} \right]\\
{u_{BM}} = 2a.\cos \left[ {\omega .\left( {t - \frac{{{d_2}}}{v}} \right)} \right]
\end{array} \right.\)
Phương trình sóng tại M là tổng hợp của hai sóng truyền tới, thực hiện tổng hợp bằng phương pháp tổng hợp fresnel.
Biên độ dao động của phần tử tại M là:
\(\begin{array}{l}
A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}.\cos \left( {\Delta \varphi } \right)} \\
\,\,\,\,\, = \sqrt {{a^2} + {{(2a)}^2} + 2a.2a.\cos \left( {2\pi .\frac{{{d_1} - {d_2}}}{\lambda }} \right)} \\
\,\,\,\,\, = \sqrt {{a^2} + {{(2a)}^2} + 2a.2a.\cos \left( {17\pi } \right)} = a
\end{array}\)
Trên bề mặt chất lỏng có hai nguồn kết hợp AB cách nhau 100cm dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số f = 10 Hz, vận tốc truyền sóng 3 m/s. Gọi M là một điểm nằm trên đường vuông góc với AB tại A, dao động với biên độ cực đại. Đoạn AM có giá trị nhỏ nhất là :
-
A
5,28 cm
-
B
10,56 cm
-
C
12 cm
-
D
30 cm
Đáp án của giáo viên lời giải hay : B
Bước sóng: \(\lambda = \dfrac{v}{f}\)
Điều kiện có cực đại giao thoa là: \({d_2} - {d_1} = k\lambda \)
Số vân giao thoa cực đại trên đoạn AB bằng số giá trị k nguyên thoả mãn: \( - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda }\)
AM nhỏ nhất khi M thuộc cực đại ứng với kmax
Áp dụng định lí Pitago trong tam giác vuông tính ra AM.
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{300}}{{10}} = 30cm\)
Số vân giao thoa cực đại trên đoạn AB bằng só giá trị k nguyên thoả mãn:
\(\begin{array}{l} - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda } \Leftrightarrow - \dfrac{{100}}{{30}} < k < \dfrac{{100}}{{30}} \Leftrightarrow - 3,3 < k < 3,3\\ \Rightarrow k = - 3; - 2;...;3\end{array}\)
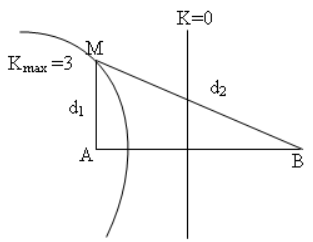
Để AM nhỏ nhất thì M phải thuộc cực đại ứng với \({k_{\max }} = 3\) như hình vẽ và thoả mãn:
\(\begin{array}{l}{d_2} - {d_1} = {k_{\max }}.\lambda \Leftrightarrow BM - AM = 3\lambda = 90cm\\ \Leftrightarrow \sqrt {A{B^2} + A{M^2}} - AM = 90\\ \Leftrightarrow \sqrt {{{100}^2} + A{M^2}} - AM = 90 \Rightarrow AM = 10,56cm\end{array}\)
Ở mặt nước, tại hai điểm A và B có hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. ABCD là hình vuông nằm ngang. Biết trên CD có 3 vị trí mà ở đó các phần tử dao động với biên độ cực đại. Trên AB có tối đa bao nhiêu vị trí mà phần tử ở đó dao động với biên độ cực đại?
-
A
13
-
B
7
-
C
11
-
D
9
Đáp án của giáo viên lời giải hay : D
Điều kiện có cực đại giao thoa trong giao thoa sóng hai nguồn cùng pha : \({d_2} - {d_1} = k\lambda \)
Số cực đại giao thoa trên đoạn AB bằng số giá trị k nguyên thoả mãn : \( - \dfrac{{AB}}{\lambda } < k < \dfrac{{AB}}{\lambda }\)
Gọi a là độ dài cạnh hình vuông ABCD.
Áp dụng định lí Pitago ta có :
\(BD = \sqrt {A{D^2} + A{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
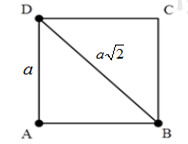
Trên CD có 3 vị trí 3 vị trí mà ở đó các phần tử dao động với biên độ cực đại nên :
\(BD - AD \le 2\lambda \Leftrightarrow a\sqrt 2 - a \le 2\lambda \Rightarrow \lambda \ge \dfrac{{a\sqrt 2 - a}}{2}\)
Ta xét tỉ số :
\(\dfrac{{AB}}{\lambda } = \dfrac{a}{\lambda } \le \dfrac{a}{{\dfrac{{a\sqrt 2 - a}}{2}}} \Leftrightarrow \dfrac{{AB}}{\lambda } \le 4,8\)
Vậy : \( - 4,8 \le k \le 4,8 \Rightarrow k = - 4; - 3;...;4\)
Vậy trên AB có tối đa 9 cực đại.
Một nguồn phát sóng cơ trên mặt nước đặt tại O, sóng có biên độ A, chu kì T, bước sóng λ. Hai điểm M, N cùng nằm trên một hướng truyền sóng cách nhau \(d = \frac{\lambda }{3}\), N gần nguồn hơn. Coi biên độ không đổi khi truyền đi. Tại thời điểm t1 = 0, M và N có li độ uM = + 3 cm và uN = - 3 cm. Ở thời điểm t2 liền sau đó, N có li độ uN = + A. Thời điểm t2 là:
-
A
\(\frac{{5T}}{6}\)
-
B
\(\frac{T}{{12}}\)
-
C
\(\frac{{11T}}{{12}}\)
-
D
\(\frac{{7T}}{{12}}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng VTLG.
Hai điểm MN cách nhau \(d = \frac{\lambda }{3}\) tức là vecto OM cách vecto ON một góc \(\frac{{2\pi }}{3}\)
Vì M và N có li độ đối xứng nhau nên ta biểu diễn được trên VTLG.
Hai điểm MN cách nhau \(d = \frac{\lambda }{3}\) tức là vecto OM cách vecto ON một góc \(\frac{{2\pi }}{3}\)
Vì M và N có li độ đối xứng nhau nên ta có hình vẽ:
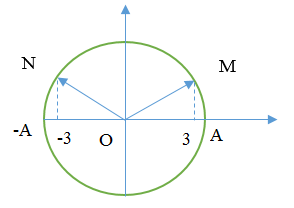
Vậy N đến vị trí có li độ A lần đầu tiên thì ON quét được một góc là:
\(\alpha = \frac{\pi }{6} + \pi = \frac{{7\pi }}{6}\)
Vậy thời gian để N có li độ A là:
\(t = \frac{\alpha }{{2\pi }}.T = \frac{7}{{12}}.T\)
Tần số của âm cơ bản và hoạ âm do một dây đàn phát ra tương ứng bằng với tần số của sóng cơ để trên dây đàn có sóng dừng. Trong các hoạ âm do dây đàn phát ra, có hai hoạ âm ứng với tần số 2640 Hz và 4400 Hz. Biết âm cơ bản của dây đàn có tần số nằm trong khoảng từ 300Hz đến 800Hz. Trong vùng tần số của âm nghe được từ 16Hz đến 20kHz, có tối đa bao nhiêu tần số của hoạ âm (kể cả âm cơ bản) của dây đàn này:
-
A
37
-
B
30
-
C
45
-
D
22
Đáp án của giáo viên lời giải hay : C
Điều kiện có sóng dừng trên dây hai đầu cố định : \(l = k{\lambda \over 2} = k{v \over {2f}} \Rightarrow f = k{v \over {2l}} = k.{f_0}\)
Trong các hoạ âm do dây đàn phát ra, có hai hoạ âm ứng với tần số 2640Hz và 4400Hz
=> Âm cơ bản phải là ước chung của 2640 và 4400
ƯC (2640 ; 4400) = {880 ; 440 ; 220 ; 110 ;…} (1)
Theo bài ra, âm cơ bản có tần số nằm trong khoảng 300Hz đến 800Hz (2)
Từ (1) và (2) => Âm cơ bản của dây đàn có tần số 440Hz
=> Các hoạ âm của dây đàn có tần số : fha =440k (k > 0 ; k nguyên)
Vùng tần số của âm nghe được từ 16Hz đến 20kHz có :
\(16Hz \le 440k \le 20000 \Leftrightarrow 0,036 \le k \le 45,45 \Rightarrow k = 1;2;3;...;45\)
=> Có tối đa 45 tần số của hoạ âm (kể cả âm cơ bản) của dây đàn.
