Đề bài
A. PHẦN TRẮC NGHIỆM (4,0 điểm, gồm 20 câu, từ câu 1 đến câu 20)
Câu 1. Hàm số \(y = - 3{x^2}\) có đồ thị hàm số là hình vẽ nào dưới đây?
A. 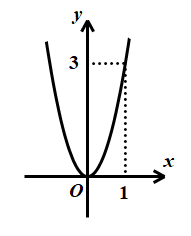
B. 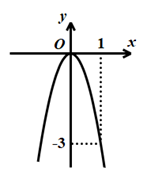
C. 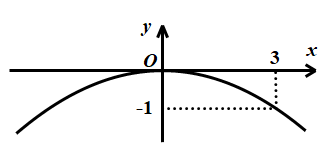
D. 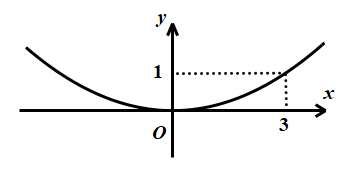
Câu 2. Hàm số nào dưới đây là hàm số bậc nhất?
A. \(y = \sqrt x + 10\) B. \(y = - 4{x^2}\) C. \(y = \dfrac{{2021}}{x}\) D. \(y = 20x - 21\)
Câu 3. Điều kiện của \(x\) để biểu thức \(\sqrt {2x + 10} \) có nghĩa là:
A. \(x \le 5\) B. \(x \ge - 5\) C. \(x \ge 5\) D. \(x \le - 5\)
Câu 4. Phương trình nào sau đây là phương trình bậc hai một ẩn?
A. \({x^3} - 4x + 6 = 0\) B. \(3x + 11 = 0\) C. \(3{x^2} - x + 5 = 0\) D. \({x^4} - 2{x^2} + 9 = 0\)
Câu 5. Cặp số \(\left( {15;16} \right)\) là nghiệm của hệ phương trình nào dưới đây?
A. \(\left\{ \begin{array}{l}x + y = - 31\\15x - 16y = 31\end{array} \right.\) B. \(\left\{ \begin{array}{l} - x + y = 1\\15x + 16y = 31\end{array} \right.\)
C. \(\left\{ \begin{array}{l} - x + y = 1\\15x + 16y = - 31\end{array} \right.\) D. \(\left\{ \begin{array}{l} - x + y = 31\\15x - 16y = - 31\end{array} \right.\)
Câu 6. Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) và \(\angle BCD = {120^0}\). Số đo của \(\angle BOD\) bằng:
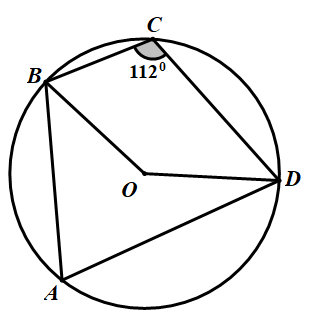
A. \({68^0}\) B. \({136^0}\) C. \({112^0}\) D. \({56^0}\)
Câu 7. Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}5x - 3y = - 5\\x - 2y = - 8\end{array} \right.\) là:
A. \(\left( { - 5; - 2} \right)\) B. \(\left( { - 2; - 5} \right)\) C. \(\left( {5;2} \right)\) D. \(\left( {2;5} \right)\)
Câu 8. Cho hàm số \(y = ax + b\) có đồ thị như hình vẽ bên dưới:
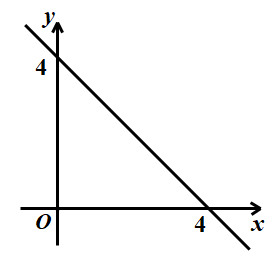
Hàm số đã cho là:
A. \(y = - x + 4\) B. \(y = x + 4\) C. \(y = - x - 4\) D. \(y = x - 4\)
Câu 9. Cho đường tròn tâm \(O\) bán kính \(12cm\) và điểm \(M\) nằm ngoài đường tròn sao cho \(MO = 20cm\). Vẽ tiếp tuyến \(MA\) với đường tròn \(\left( O \right)\) (\(A\) là tiếp điểm). Độ dài của đoạn thẳng \(MA\) bằng:
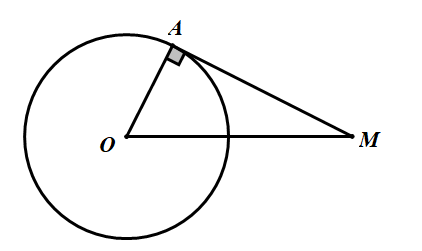
A. \(16cm\) B. \(20cm\) C. \(256cm\) D. \(8cm\)
Câu 10. Một cột cờ cao \(7,8m\) có bóng trên mặt đất dài \(13m\) (minh họa như hình vẽ). Số đo góc \(\alpha \) mà tia sáng mặt trời tại với mặt đất (làm tròn đến độ) bằng:
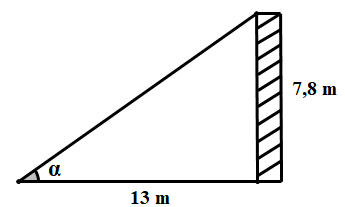
A. \({31^0}\) B. \({59^0}\) C. \({37^0}\) D. \({53^0}\)
Câu 11. Gọi \(S\) và \(P\) lần lượt là tổng và tích hai nghiệm của phương trình \({x^2} - 4x - 7 = 0\). Giá trị của biểu thức \(S.P\) bằng:
A. \( - 14\) B. \(14\) C. \( - 28\) D. \(28\)
Câu 12. Cho đường tròn tâm \(O\) bán kinh \(4cm\). Độ dài của đường tròn \(\left( O \right)\) bằng:
A. \(8\pi \,cm\) B. \(16\pi \,cm\) C. \(2\pi \,cm\) D. \(4\pi \,cm\)
Câu 13. Thể tích của hình cầu có bán kính \(15cm\) bằng:
A. \(13500\pi \,c{m^3}\) B. \(900\pi \,c{m^3}\) C. \(300\pi \,c{m^3}\) D. \(4500\pi \,c{m^3}\)
Câu 14. Tọa độ giao điểm của đường thẳng \(\left( d \right):y = - 2x + 3\) và parabol \(\left( P \right):y = {x^2}\) là:
A. \(\left( {1; - 1} \right)\) và \(\left( { - 3;9} \right)\) B. \(\left( { - 1; - 1} \right)\) và \(\left( { - 3;9} \right)\) C. \(\left( {1;1} \right)\) và \(\left( { - 3;9} \right)\) D. \(\left( {1;1} \right)\) và \(\left( { - 3; - 9} \right)\)
Câu 15. Giá trị của biểu thức \(5\sqrt {144} - \sqrt[3]{{15625}} + 7\) bằng:
A. \(92\) B. \( - 72\) C. \(42\) D. \( - 58\)
Câu 16. Bạn Lan đi siêu thị mua hai loại trái cây là xoài và ổi. Số tiền mà Lan phải trả theo giá niêm yết khi mua \(2kg\) xoài và \(3kg\) ổi là \(80\,000\) đồng. Tuy nhiên, khi Lan trả tiền thì giá niêm yết của xoài được giảm \(10\% \) so với giá niêm yết. Do đó, Lan chỉ trả \(75\,000\) đồng. Giá niêm yết của mỗi \(kg\) xoài và \(kg\) ổi lần lượt là:
A. \(10\,000\) đồng và \(25\,000\) đồng B. \(28\,000\) đồng và \(8\,000\) đồng
C. \(16\,000\) đồng và \(16\,000\) đồng D. \(25\,000\)đồng và \(10\,000\) đồng
Câu 17. Cho đường thẳng \(\left( {{d_1}} \right):y = ax + b\) đi qua điểm \(M\left( {0;5} \right)\) và đồng thời song song với đường thẳng \(\left( {{d_2}} \right):y = 2x - \dfrac{3}{4}\). Giá trị của \(a\) và \(b\) là:
A. \(a = - \dfrac{3}{4}\) và \(b = 2\) B. \(a = 2\) và \(b = 5\) C. \(a = 5\) và \(b = 2\) D. \(a = 2\) và \(b = - \dfrac{3}{4}\)
Câu 18. Tất cả giá trị của tham số \(m\) sao cho hệ phương trình \(\left\{ \begin{array}{l}x + \left( {m - 3} \right)y = 2\\x - 6y = 4\end{array} \right.\) có nghiệm duy nhất là:
A. \(m \ne 9\) B. \(m \ne - 3\) C. \(m \ne 3\) D. \(m \ne - 9\)
Câu 19. Giá trị của tham số \(m\) sao cho phương trình \(2{x^2} + 4x + m + 4 = 0\) có nghiệm kép là:
A. \(m = - 2\) B. \(m = 2\) C. \(m = 6\) D. \(m = - 6\)
Câu 20. Một lon sữa hình trụ có đường kính đáy \(1,2dm\) và chiều cao \(1,8dm\). Diện tích nhãn dán xung quanh (không kể mép dán) của lon sữa đó (kết quả làm tròn 2 chữ số thập phân và lấy giá trị gần đúng của \(\pi \) bằng \(3,14\)) là:
A. \(15,56d{m^2}\) B. \(2,16d{m^2}\) C. \(6,78d{m^2}\) D. \(4,07d{m^2}\)
B. PHẦN TỰ LUẬN (6,0 điểm, gồm 4 câu, từ câu 1 đến câu 4)
Câu 1 (1,0 điểm):
Giải phương trình và hệ phương trình sau:
a) \({x^2} - 5x + 6 = 0\)
b) \(\left\{ \begin{array}{l}x + 2y = 21\\3x - y = 7\end{array} \right.\)
Câu 2 (1,0 điểm):
a) Rút gọn biểu thức \(A = \dfrac{{\sqrt {15} - \sqrt 3 }}{{\sqrt 5 - 1}} - \dfrac{1}{{2 - \sqrt 3 }}\)
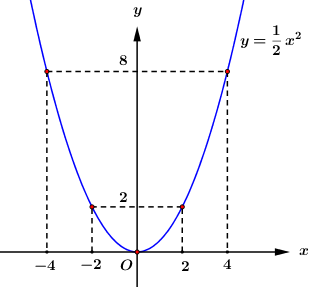
b) Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\)
Câu 3 (1,5 điểm):
a) Tìm tất cả giá trị của tham số m sao cho phương trình \({x^2} - mx - m - 1 = 0\) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = {x_1} + {x_2}\).
b) Trong năm học 2020-2021, trường Trung học cơ sở A tổ chức cho học sinh đăng ký tham gia câu lạc bộ Toán học và câu lạc bộ Sáng tạo khoa học. Ở học kỳ 1, số lượng học sinh tham gia câu lạc bộ Toán học ít hơn số lượng học sinh tham gia câu lạc bộ Sáng tạo khoa học là 50 học sinh. Sang học kỳ 2, có 5 học sinh chuyển từ câu lạc bộ Sáng tạo khoa học sang câu lạc bộ Toán học nên số lượng học sinh của câu lạc bộ Toán học bằng \(\dfrac{3}{4}\) số lượng học sinh của câu lạc bộ Sáng tạo khoa học. Biết rằng trong năm học, tổng số học sinh tham gia cả hai câu lạc bộ không thay đổi và mỗi học sinh chỉ tham gia một câu lạc bộ. Hỏi số lượng học sinh của mỗi câu lạc bộ ở học kì 2 là bao nhiêu?
Câu 4 (2,5 điểm):
Cho tam giác \(ABC\)\(\left( {AB < AC} \right)\) có ba góc nhọn và nội tiếp đường tròn \(\left( O \right)\). Các đường cao \(AD,BE,CF\)của tam giác \(ABC\) cắt nhau tại \(H\).
a) Chứng minh rằng tứ giác \(BCEF\), \(EHDC\) nội tiếp.
b) Gọi \(K\) là giao điểm của hai đường thẳng \(EF\) và \(BC\). Đường thẳng \(AK\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(I\). Chứng minh rằng \(KBF\) đồng dạng với tam giác \(KEC\) và \(KI.KA = KF.KE\).
c) Qua điểm \(B\) vẽ đường thẳng song song với đường thẳng \(AC\) cắt các đường thẳng \(AK\) và \(AH\) lần lượt tại \(M\) và \(N\). Chứng minh \(HM = HN\).
Câu 2
A. PHẦN TRẮC NGHIỆM (4,0 điểm, gồm 20 câu, từ câu 1 đến câu 20)
|
1. B |
2. D |
3. B |
4. C |
5. D |
6. B |
7. D |
8. A |
9. A |
10. A |
|
11. C |
12. A |
13. D |
14. C |
15. C |
16. D |
17. B |
18. B |
19. A |
20. C |
Câu 1
Phương pháp:
Vận dụng kiến thức về đồ thị hàm số bậc hai một ẩn.
Cách giải:
\(a = - 3 < 0\) nên parabol có bề lõm hướng xuống dưới
Đồ thị hàm số đi qua điểm \(\left( {0;0} \right)\)
Đồ thị hàm số đi qua điểm \(\left( {1; - 3} \right)\)
Chọn B.
Câu 2
Phương pháp:
Vận dụng định nghĩa hàm số bậc nhất: Hàm số bậc nhất là hàm số được cho bởi công thức \(y = ax + b\) trong đó \(a,b\) là cho trước và \(a \ne 0\).
Cách giải:
Từ định nghĩa của hàm số bậc nhất: Hàm số \(y = 20x - 21\) là hàm số bậc nhất.
Chọn D.
Câu 3
Phương pháp:
Biểu thức \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)
Cách giải:
Biểu thức \(\sqrt {2x + 10} \) có nghĩa \( \Leftrightarrow 2x + 10 \ge 0 \Leftrightarrow x \ge - 5\)
Chọn B.
Câu 4
Phương pháp:
Vận dụng định nghĩa phương trình bậc hai một ẩn: Phương trình bậc hai một ẩn là phương trình có dạng \(a{x^2} + bx + c = 0\). Trong đó \(x\) là ẩn số và \(a,b,c\) là những số cho trước gọi là các hệ số, \(a \ne 0\).
Cách giải:
Từ định nghĩa của phương trình bậc hai một ẩn: Phương trình \(3{x^2} - x + 5 = 0\) là phương trình bậc hai một ẩn.
Chọn C.
Câu 5
Phương pháp:
Cách làm tự luận: Sử dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình.
Cách làm trắc nghiệm: Sử dụng máy tính bỏ túi, thay cặp số \(\left( {15;16} \right)\) vào từng hệ phương trình để xác định cặp số \(\left( {15;16} \right)\) có là nghiệm của hệ phương trình hay không.
Cách giải:
Vận dụng cách làm bài trắc nghiệm, cặp số \(\left( {15;16} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l} - x + y = 31\\15x - 16y = - 31\end{array} \right.\).
Chọn D.
Câu 6
Phương pháp:
Vận dụng tính chất tổng hai góc đổi của một tứ giác nội tiếp bằng \({180^0}\).
Sử dụng mối quan hệ giữa góc nội tiếp và góc ở tâm cùng chắn một cung trong một đường tròn.
Cách giải:
Tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \(\angle BCD + \angle BAD = {180^0}\) (tính chất của tứ giác nội tiếp)
\(\angle BAD = {180^0} - \angle BCD = {180^0} - {112^0} = {68^0}\)
Xét đường tròn \(\left( O \right)\) có: \(\angle BAD = \dfrac{1}{2}\angle BOD\) (hai góc này cùng chắn cung \(BD\))
Suy ra \(\angle BOD = 2\angle BAD = {2.68^0} = {136^0}\)
Vậy \(\angle BOD = {136^0}\)
Chọn B.
Câu 7
Phương pháp:
Sử dụng phương pháp thế để tìm nghiệm của hệ phương trình.
Cách giải:
\(\left\{ \begin{array}{l}5x - 3y = - 5\\x - 2y = - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x - 3y = - 5\,\,\,\left( 1 \right)\\x = 2y - 8\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Thay (2) và (1), ta được: \(5\left( {2y - 8} \right) - 3y = - 5\)
\(\begin{array}{l} \Leftrightarrow 10y - 40 - 3y = - 5\\ \Leftrightarrow 7y = 35\\ \Leftrightarrow y = 5\end{array}\)
Với \(y = 5\) thay vào (2), ta được: \(x = 2.5 - 8 = 10 - 8 = 2\)
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {2;5} \right)\)
Chọn D.
Câu 8
Phương pháp:
Đọc được các yếu tố có được từ hình vẽ của đồ thị hàm số bậc nhất.
Cách giải:
Đồ thị hàm số đi qua hai điểm \(\left( {0;4} \right)\) và \(\left( {4;0} \right)\), nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}0.a + b = 4\\4.a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = - \dfrac{b}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = - 1\end{array} \right.\)
Vậy hàm số cần tìm là: \(y = - x + 4\)
Chọn A.
Câu 9
Phương pháp:
Sử dụng định lí Py – ta – go để tính độ dài cạnh của tam giác vuông.
Cách giải:
\(MA\) là tiếp tuyến với đường tròn \(\left( O \right)\) nên \(OA \bot AM \Rightarrow \angle OAM = {90^0}\)
Vậy \(\Delta OAM\) vuông tại \(A\), theo định lí Py – ta – go ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,O{M^2} = O{A^2} + A{M^2}\\ \Leftrightarrow A{M^2} = O{M^2} - O{A^2}\\ \Leftrightarrow A{M^2} = {20^2} - {12^2}\\ \Leftrightarrow A{M^2} = 256\\ \Leftrightarrow AM = 16\left( {cm} \right)\end{array}\)
Vậy \(MA = 16cm\)
Chọn A.
Câu 10
Phương pháp:
Vận dụng định nghĩa về tỷ số lượng giác của góc nhọn
Cách giải:
Ta có: \(\tan \alpha = \dfrac{{7,8}}{{13}} = \dfrac{3}{5} \Rightarrow \alpha = {30^0}57'50'' \approx {31^0}\)
Chọn A.
Câu 11
Phương pháp:
Cách 1: Tìm các nghiệm của phương trình ban đầu, sau đó tính \(S\) và \(P\) để suy ra giá trị của biểu thức \(S.P\).
Cách 2: Áp dụng hệ thức Vi – ét để tính giá trị của biểu thức \(S.P\).
Cách giải:
\({x^2} - 4x - 7 = 0\)
Ta có: \(\Delta ' = {\left( { - 2} \right)^2} - 1.\left( { - 7} \right) = 4 + 7 = 11 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).
Theo hệ thức Vi – ét, ta có: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \dfrac{{ - \left( { - 4} \right)}}{1} = 4\\P = {x_1}.{x_2} = \dfrac{{ - 7}}{1} = - 7\end{array} \right.\)
Khi đó, \(S.P = 4.\left( { - 7} \right) = - 28\)
Chọn C.
Câu 12
Phương pháp:
Áp dụng công thức tính chu vi của hình tròn có bán kính \(r\) là: \(C = 2\pi r\)
Cách giải:
Độ dài của đường tròn \(\left( O \right)\) là: \(2\pi .4 = 8\pi \left( {cm} \right)\)
Chọn A.
Câu 13
Phương pháp:
Áp dụng công thức tính thể tích hình cầu có bán kính bằng \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\)
Cách giải:
Thể tích của hình cầu là: \(V = \dfrac{4}{3}\pi {.15^3} = 4500\pi \,\left( {c{m^3}} \right)\)
Chọn D.
Câu 14
Phương pháp:
Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\), sau đó đưa phương trình đó về phương trình tích để tìm giao điểm.
Cách giải:
Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\), ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} = - 2x + 3\\ \Leftrightarrow {x^2} + 2x - 3 = 0\\ \Leftrightarrow {x^2} - x + 3x - 3 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 3\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 1\\x = - 3 \Rightarrow y = 9\end{array} \right.\end{array}\)
Vậy tọa độ giao điểm của đường thẳng \(\left( d \right):y = - 2x + 3\) và parabol \(\left( P \right):y = {x^2}\) là: \(\left( {1;1} \right)\) và \(\left( { - 3;9} \right)\).
Chọn C.
Câu 15
Phương pháp:
Vận dụng định nghĩa căn thức bậc hai, căn bậc ba để rút gọn tính giá trị biểu thức.
Cách giải:
\(\begin{array}{l}\,\,\,\,\,5\sqrt {144} - \sqrt[3]{{15625}} + 7\\ = 5\sqrt {{{12}^2}} - \sqrt[3]{{{{25}^3}}} + 7\\ = 5.12 - 25 + 7\\ = 60 - 25 + 7\\ = 42\end{array}\)
Chọn C.
Câu 16
Phương pháp:
Giải bài toán bằng cách lập hệ phương trình, cụ thể:
Gọi giá niêm yết của mỗi \(kg\) xoài là \(x\,\,\left( {x > 0} \right)\); giá niêm yết của mỗi \(kg\) ổi là \(y\,\,\left( {y > 0} \right)\), dựa vào giả thiết để thiết lập hệ phương trình.
Giải hệ phương trình bằng phương pháp cộng đại số và phương pháp thế.
Cách giải:
Gọi giá niêm yết của mỗi \(kg\) xoài là \(x\,\,\left( {x > 0} \right)\)
giá niêm yết của mỗi \(kg\) ổi là \(y\,\,\left( {y > 0} \right)\)
Vì số tiền mà Lan phải trả theo giá niêm yết khi mua \(2kg\) xoài và \(3kg\) ổi là \(80\,000\) đồng nên ta có phương trình: \(2x + 3y = 80\,000\,\,\,\,\left( 1 \right)\)
Vì khi Lan trả tiền thì giá niêm yết của xoài được giảm \(10\% \) so với giá niêm yết. Do đó, Lan chỉ trả \(75\,000\) đồng nên ta có phương trình: \(2.90\% .x + 3y = 75\,000\,\,\,\,\left( 2 \right)\)
Từ (1) và (2), ta có hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y = 80\,000\\2.90\% .x + 3y = 75000\,\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 3y = 80\,000\\1,8x + 3y = 75\,000\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2x + 3y = 80\,000\\0,2x = 5\,000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{{80\,000 - 2x}}{3}\\x = 25\,000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 10\,000\\x = 25\,000\end{array} \right.\) (tmđk)
Vậy giá niêm yết của mỗi \(kg\) xoài và \(kg\) ổi lần lượt là: \(25\,000\)đồng và \(10\,000\) đồng
Chọn D.
Câu 17
Phương pháp:
Thiết lập điều kiện khi hai đường thẳng song song với nhau.
Thay tọa độ điểm \(M\left( {0;5} \right)\) vào phương trình đường thẳng \(\left( {{d_1}} \right)\).
Cách giải:
Vì đường thẳng \(\left( {{d_1}} \right):y = ax + b\) song song với đường thẳng \(\left( {{d_2}} \right):y = 2x - \dfrac{3}{4}\) nên \(a = 2\) và \(b \ne - \dfrac{3}{4}\)
Suy ra, phương trình đường thẳng \(\left( {{d_1}} \right)\) có dạng \(y = 2x + b\) với \(b \ne - \dfrac{3}{4}\)
Theo giả thiết \(\left( {{d_1}} \right)\) đi qua điểm \(M\left( {0;5} \right)\) nên ta có: \(2.0 + b = 5 \Rightarrow b = 5\)
Vậy \(a = 2\) và \(b = 5\)
Chọn B.
Câu 18
Phương pháp:
Vận dụng phương pháp cộng đại số để tìm điều kiện phương trình có nghiệm duy nhất
Cách giải:
\(\left\{ \begin{array}{l}x + \left( {m - 3} \right)y = 2\\x - 6y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m + 3} \right)y = - 2\,\,\,\left( 1 \right)\\x - 6y = 4\,\,\,\left( 2 \right)\end{array} \right.\)
Để hệ phương trình có nghiệm duy nhất thì phương trình (1) phải có nghiệm duy nhất \( \Leftrightarrow m + 3 \ne 0 \Leftrightarrow m \ne - 3\)
Vậy với \(m \ne - 3\) thì hệ phương trình có nghiệm duy nhất.
Chọn B.
Câu 19
Phương pháp:
Phương trình có nghiệm kép \( \Leftrightarrow \Delta = 0\) (hoặc \(\Delta ' = 0\))
Cách giải:
Phương trình có nghiệm kép \( \Leftrightarrow \Delta ' = 0\)
\(\begin{array}{l} \Leftrightarrow {2^2} - 2.\left( {m + 4} \right) = 0\\ \Leftrightarrow 2 - m - 4 = 0\\ \Leftrightarrow - m - = 0\\ \Leftrightarrow m = - 2\end{array}\)
Vậy \(m = - 2\) thỏa mãn yêu cầu của đề bài.
Chọn A.
Câu 20
Phương pháp:
Áp dụng công thức tính diện tích toàn phần của hình trụ.
Cách giải:
Bán kinh đáy của lon sữa là: \(1,2:2 = 0,6dm\)
Diện tích nhãn dán xung quanh của lon sữa đó là: \(2\pi .0,6.1,8 = 2,16\pi \approx 6,78d{m^2}\)
Chọn C.
B. PHẦN TỰ LUẬN (6,0 điểm, gồm 4 câu, từ câu 1 đến câu 4)
Câu 1
Phương pháp:
a) Vận dụng công thức nghiệm bậc hai để tìm nghiệm của phương trình.
b) Vận dụng phương pháp cộng đại số và phương pháp thế để tìm nghiệm của hệ phương trình.
Cách giải:
a) \({x^2} - 5x + 6 = 0\)
Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.6 = 1 > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{5 + 1}}{2} = 3\\{x_2} = \dfrac{{5 - 1}}{2} = 2\end{array} \right.\).
Vậy tập nghiệm của phương trình là \(S = \left\{ {2;3} \right\}\).
b) \(\left\{ \begin{array}{l}x + 2y = 21\\3x - y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 6y = 63\\3x - y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7y = 56\\x = 21 - 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 8\\x = 21 - 2.8 = 5\end{array} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {5;8} \right)\).
Câu 2
Phương pháp:
a) Đặt nhân tử chung, trục căn thức ở mẫu để rút gọn và tính giá trị của biểu thức.
b) Nhận xét hệ số \(a\) của hàm số để nhận biết bề lõm của đồ thị.
Lập bảng giá trị của \(x\) và \(y\) để xác định tọa độ điểm để vẽ đồ thị hàm số.
Cách giải:
a) Rút gọn biểu thức \(A = \dfrac{{\sqrt {15} - \sqrt 3 }}{{\sqrt 5 - 1}} - \dfrac{1}{{2 - \sqrt 3 }}\)
\(\begin{array}{l}A = \dfrac{{\sqrt {15} - \sqrt 3 }}{{\sqrt 5 - 1}} - \dfrac{1}{{2 - \sqrt 3 }}\\A = \dfrac{{\sqrt 3 \left( {\sqrt 5 - 1} \right)}}{{\sqrt 5 - 1}} - \dfrac{{2 + \sqrt 3 }}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}\\A = \sqrt 3 - \dfrac{{2 + \sqrt 3 }}{{4 - 3}}\\A = \sqrt 3 - 2 - \sqrt 3 \\A = - 2\end{array}\)
Vậy \(A = - 2\).
b) Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\)
Parabol \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) có bề lõm hướng lên và nhận \(Oy\) làm trục đối xứng.
Ta có bảng giá trị sau:
|
\(x\) |
\( - 4\) |
\( - 2\) |
\(0\) |
2 |
4 |
|
\(y = \dfrac{1}{2}{x^2}\) |
8 |
2 |
0 |
2 |
8 |
\( \Rightarrow \) Parabol \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) đi qua các điểm \(\left( { - 4;8} \right)\), \(\left( { - 2;2} \right)\), \(\left( {0;0} \right)\), \(\left( {2;2} \right)\), \(\left( {4;8} \right)\).
Đồ thị Parabol \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\):
Câu 3
Phương pháp:
a) Phương trình có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\)
Áp dụng hệ thức Vi – ét , xác định \({x_1} + {x_2}\) và \({x_1}.{x_2}\), thay vào biểu thức của đề bài để tìm ra giá trị của \(m\).
b) Giải bài toán bằng cách lập phương trình, cụ thể gọi số lượng học sinh tham gia câu lạc bộ Toán học ở học kì 1 là \(x\) học sinh \(\left( {x \in \mathbb{N}*} \right)\), dựa vào giả thiết của đề bài để lập phương trình.
Cách giải:
a) Phương trình \({x^2} - mx - m - 1 = 0\) có 2 nghiệm phân biệt \({x_1},{x_2}\)
\(\begin{array}{l} \Leftrightarrow \Delta = {b^2} - 4ac > 0\\ \Leftrightarrow {\left( { - m} \right)^2} - 4.1.\left( { - m - 1} \right) > 0\\ \Leftrightarrow {m^2} + 4m + 4 > 0\\ \Leftrightarrow {\left( {m + 2} \right)^2} > 0\\ \Leftrightarrow m \ne - 2\,\,\,\left( 1 \right)\end{array}\)
Khi đó, theo hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}.{x_2} = - m - 1\end{array} \right.\)
Theo bài ra ta có:
\(\begin{array}{l}\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = {x_1} + {x_2} \Leftrightarrow \dfrac{{{x_1} + {x_2}}}{{{x_1}.{x_2}}} = {x_1} + {x_2}\\ \Leftrightarrow \dfrac{{{x_1} + {x_2}}}{{{x_1}.{x_2}}} - \left( {{x_1} + {x_2}} \right) = 0 \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left( {\dfrac{1}{{{x_1}{x_2}}} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_1} + {x_2} = 0\\\dfrac{1}{{{x_1}{x_2}}} - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x_1} + {x_2} = 0\\\dfrac{1}{{{x_1}{x_2}}} = 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x_1} + {x_2} = 0\\{x_1}{x_2} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\ - m - 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,\,\,\left( {tm} \right)\\m = - 2\,\,\,\,\left( {ktm\left( 1 \right)} \right)\end{array} \right.\end{array}\)
Vậy \(m = 0\) là giá trị cần tìm.
b) Gọi số lượng học sinh tham gia câu lạc bộ Toán học ở học kì 1 là \(x\) học sinh \(\left( {x \in \mathbb{N}*} \right)\)
Vì số lượng học sinh tham gia câu lạc bộ Toán học ít hơn số lượng học sinh tham gia câu lạc bộ Sáng tạo khoa học là 50 học sinh nên số học sinh tham gia câu lạc bộ Sáng tạo khoa học ở học kì 1 là \(x + 50\) (học sinh).
Học kì 2, số học sinh tham gia câu lạc bộ Sáng tạo khoa học và câu lạc bộ Toán học lần lượt là: \(x + 50 - 5 = x + 45\) (học sinh) và \(x + 5\) (học sinh).
Do số lượng học sinh của câu lạc bộ Toán học bằng \(\dfrac{3}{4}\) số lượng học sinh của câu lạc bộ Sáng tạo khoa học nên ta có phương trình
\(x + 5 = \dfrac{3}{4}.\left( {x + 45} \right)\)\( \Leftrightarrow x + 5 = \dfrac{3}{4}x + \dfrac{{135}}{4} \Leftrightarrow \dfrac{x}{4} = \dfrac{{115}}{4} \Leftrightarrow x = 115\)(TMĐK)
Vậy học kì 2, số lượng học sinh tham gia câu lạc bộ Toán học là \(115 + 5 = 120\) học sinh, số học sinh tham gia câu lạc bộ Sáng tạo khoa học là \(115 + 45 = 160\) học sinh.
Câu 4
Phương pháp:
a) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp.
b) Áp dụng kiến thức về góc – đường tròn và tam giác đồng dạng.
c) Áp dụng kiến thức về góc – đường tròn, tam giác đồng dạng và tính chất của các đường trong tam giác.
Cách giải:
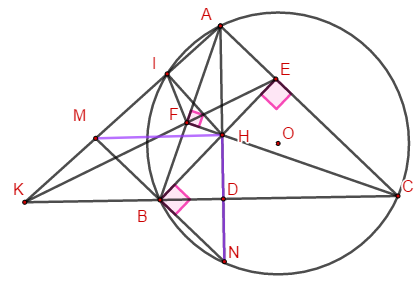
a) +) Xét tứ giác \(BFEC\) có: \(\angle BFC = \angle BEC = {90^0}\,\,\left( {gt} \right)\)
Suy ra tứ giác \(BFEC\) nội tiếp (Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
+) Xét tứ giác \(EHDC\) có: \(\angle HDC + \angle HEC = {90^0} + {90^0} = {180^0}\) suy ra \(HDCE\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Ta có:
Tứ giác \(BFCE\) nội tiếp nên \(\angle KFB = \angle KCE\)(góc ngoài và góc trong đỉnh đối diện của tứ giác nội tiếp).
Xét \(\Delta KBF\) và \(\Delta KEC\) có: \(\left\{ \begin{array}{l}\angle KFB = \angle KCE\,\,\left( {cmt} \right)\\\angle BKF = \angle CKE\end{array} \right.\) \( \Rightarrow \Delta KBF \sim \Delta KEC\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{KB}}{{KE}} = \dfrac{{KF}}{{KC}}\) (hai cạnh tương ứng) \( \Rightarrow KF.KE = KB.KC\,\,\,\left( 1 \right)\)
Trong \(\left( O \right)\) có \(\angle KAB = \angle KCI\)( hai góc nội tiếp cùng chắn cung \(BI\)).
Xét \(\Delta KAB\) và \(\Delta KCI\) có: \(\left\{ \begin{array}{l}\angle AKB = \angle CKI\\\angle KAB = \angle KCI\,\,\left( {cmt} \right)\end{array} \right.\) \( \Rightarrow \Delta KAB \sim \Delta KCI\,\,\left( {g.g} \right)\).
\( \Rightarrow \dfrac{{KA}}{{KC}} = \dfrac{{KB}}{{KI}}\) (2 cạnh tương ứng) \( \Rightarrow KA.KI = KB.KC\,\,\left( 2 \right)\)
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow KI.KA = KE.KF\) (đpcm).
c) Ta có: \(KI.KA = KF.KE\,\,\left( {cmt} \right) \Rightarrow \dfrac{{KI}}{{KE}} = \dfrac{{KF}}{{KA}}\).
Xét \(\Delta KIF\) và \(\Delta KEA\) ta có:
\(\dfrac{{KI}}{{KE}} = \dfrac{{KF}}{{KA}}\) (cmt);
\(\angle AKE\) chung;
\( \Rightarrow \Delta KIF \sim \Delta KEA\,\,\left( {c.g.c} \right)\)\( \Rightarrow \angle KIF = \angle FEA\) (2 góc tương ứng).
\( \Rightarrow AIFE\) là tứ giác nội tiếp (Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện).
\( \Rightarrow I,{\rm{ }}A,{\rm{ }}F,{\rm{ }}E\) cùng thuộc một đường tròn.
Mà tứ giác \(AEHF\) là tứ giác nội tiếp (do có \(\angle AEH + \angle AFH = {180^0}\)) \( \Rightarrow A,\,\,E,\,\,H,\,\,F\) cùng thuộc 1 đường tròn.
Do đó 5 điểm \(I,{\rm{ }}A,{\rm{ }}F,{\rm{ }}H,{\rm{ }}E\)cùng nội tiếp đường tròn đường kính \(AH\).
\( \Rightarrow \angle HIA = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
\( \Rightarrow HI \bot AK\)\( \Rightarrow \angle HIM = {90^0}\)(kề bù với \(\angle HIA\)).
Ta có: \(\left\{ \begin{array}{l}BE \bot AC\,\,\left( {gt} \right)\\AC//MN\,\,\left( {gt} \right)\end{array} \right. \Rightarrow BE \bot MN\) (từ vuông góc đến song song) \( \Rightarrow \angle HBM = {90^0}\).
\( \Rightarrow \angle HIM = \angle HBM = {90^0} \Rightarrow \angle HIM + \angle HBM = {180^0}\)
\( \Rightarrow BHIM\) nội tiếp đường tròn đường kính \(HM\) (dhnb).
\( \Rightarrow \angle MHB = \angle MIB = \angle KIB\) (2 góc nội tiếp cùng chắn cung \(BM\)).
Mà \(\angle KIB = \angle KCA\) (vì \(\angle KIB\) là góc ngoài tại đỉnh \(I\)của tứ giác nội tiếp \(BIAC\)) \( \Rightarrow \angle MHB = \angle KCA\).
Mặt khác ta có: \(\angle KCA = \angle AHE\) (cùng phụ \(\angle HAE\)) và \(\angle AHE = \angle BHN\)(đối đỉnh)
\( \Rightarrow \angle MHB = \angle BHN\) \( \Rightarrow HB\) là tia phân giác của góc \(MHN\).
\( \Rightarrow \) Tam giác \(MHN\)cân tại \(H\) (do có \(HB\) là đường cao đồng thời là đường phân giác).
Vậy \(HM = HN\).
