Đề bài
Bài 1 (2,0 điểm):
1) Thực hiện phép tính \(7\sqrt {16} + 2\sqrt 9 \)
2) Cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\)
a) Vẽ \(\left( P \right)\)
b) Bằng phép tính tìm tọa độ giao điểm giữa \(\left( P \right)\) và đường thẳng \(\left( d \right):y = - x + 2\).
Bài 2 (2,0 điểm):
1. Giải phương trình và hệ phương trình sau:
a) \({x^2} + x - 12 = 0\)
b) \(\left\{ {\begin{array}{*{20}{c}}{2x - y = - 3}\\{x + 3y = 4}\end{array}} \right.\)
2. Cho phương trình (ẩn \(x\)): \({x^2} - 2\left( {m + 2} \right)x + {m^2} + 7 = 0\)
a) Tìm \(m\) để phương trình có 2 nghiệm phân biệt.
b) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm phân biệt của phương trình. Tìm \(m\) để \({x_1}^2 + {x_2}^2 = {x_1}{x_2} + 12\).
Bài 3 (1,5 điểm):
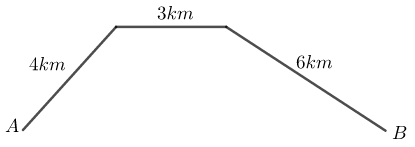
Quãng đường AB gồm một đoạn lên dốc dài 4km, một đoạn bằng phẳng dài 3 km và một đoạn xuống dốc dài 6km (như hình vẽ). Một người đi xe đạp từ A đến B và quay về A ngay hết tổng cộng 130 phút. Biết rằng vận tốc người đó đi trên đoạn đường bằng phẳng là 12km/h và vận tốc xuống dốc lớn hơn vận tốc lên dốc 5km/h (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và vận tốc lúc xuống dốc của người đó.
Bài 4 (3,5 điểm):
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(S\) nằm bên ngoài đường tròn, \(SO = d\). Kẻ các tiếp tuyến \(SA,SB\) với đường tròn (\(A,B\)là các tiếp điểm).
a) Chứng minh rằng \(4\) điểm \(S,O,A,B\) cùng thuộc một đường tròn.
b) Trong trường hợp \(d = 2R\), tính độ dài đoạn thẳng \(AB\) theo \(R\).
c) Gọi \(C\) là điểm đối xứng của \(B\) qua \(O\). Đường thẳng \(SC\) cắt đường tròn \(\left( O \right)\) tại \(D\)( khác \(C\)). Hai đường thẳng \(AD\) và \(SO\) cắt nhau tại \(M\). Chứng minh rằng \(S{M^2} = MD.MA\).
d) Tìm mối liên hệ giữa \(d\) và \(R\) để tứ giác \(OAMB\) là hình thoi.
Bài 5 (1,0 điểm):
Cho \(x\) là số thực bất kì. Tìm GTNN của biểu thức: \(T = \dfrac{{{x^2} + 7}}{{\sqrt {{x^2} + 3} }} + \dfrac{{\sqrt {{x^2} + 3} }}{{{x^2} + 7}}\)
Lời giải chi tiết
Bài 1:
Phương pháp:
1) Vận dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\) để biến đổi, rút gọn biểu thức
2) a) Lập bảng giá trị của \(x\) và \(y\), tìm được các điểm mà \(\left( P \right)\) đi qua từ đó vẽ được đồ thị hàm số \(\left( P \right)\).
b) Xét phương trình hoành độ giao điểm giữa \(\left( P \right)\) và đường thẳng \(\left( d \right)\)
Tìm nghiệm của phương trình, suy ra tọa độ giao điểm của \(\left( P \right)\) và đường thẳng \(\left( d \right)\).
Cách giải:
1) Ta có: \(7\sqrt {16} + 2\sqrt 9 = 7.4 + 2.3 = 34\).
2)
a) Parabol \(\left( P \right):\,\,y = {x^2}\) có bề lõm hướng lên và nhận \(Oy\) làm trục đối xứng.
Ta có bảng giá trị sau:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
1 |
2 |
|
\(y = {x^2}\) |
4 |
1 |
0 |
1 |
4 |
\( \Rightarrow \) Parabol \(\left( P \right):\,\,y = {x^2}\) đi qua các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\).
Đồ thị Parabol \(\left( P \right):\,\,y = {x^2}\):
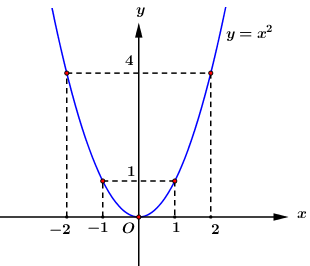
b) Xét phương trình hoành độ giao điểm giữa \(\left( P \right)\) và đường thẳng \(\left( d \right)\) ta được:
\({x^2} = - x + 2 \Leftrightarrow {x^2} + x - 2 = 0\)
Ta có: \(a + b + c = 1 + 1 - 2 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = 1\\x = \dfrac{c}{a} = - 2\end{array} \right.\)
Với \(x = 1\) ta có \(y = {1^2} = 1\).
Với \(x = - 2\) ta có \(y = {\left( { - 2} \right)^2} = 4\).
Vậy đồ thị \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm \(\left( {1;1} \right),\,\,\left( { - 2;4} \right)\).
Bài 2:
Phương pháp:
1) a) Vận dụng công thức nghiệm của phương trình bậc hai để tìm nghiệm của phương trình.
b) Phối hợp phương pháp cộng đại số và phương pháp thế để giải hệ phương trình.
2) a) Phương trình bậc hai một ẩn có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0\,\left( {\Delta ' > 0} \right)\)
b) Vận dụng hệ thức Vi – ét để tìm \({x_1} + {x_2};{x_1}.{x_2}\) sau đó thay vào hệ thức của đề bài để tìm giá trị tham số \(m\).
Cách giải:
1)
|
a) \({x^2} + x - 12 = 0\) Phương trình \({x^2} + x - 12 = 0\) có: \(\Delta = 1 - 4.1.( - 12) = 49 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 1 + \sqrt {49} }}{2} = 3\\{x_2} = \dfrac{{ - 1 - \sqrt {49} }}{2} = - 4\end{array} \right.\) Vậy phương trình có tập nghiệm: \(S = \left\{ {3; - 4} \right\}\). |
b) \(\left\{ {\begin{array}{*{20}{c}}{2x - y = - 3}\\{x + 3y = 4}\end{array}} \right.\) Ta có: \(\begin{array}{l}\,\,\,\,\,\,\left\{ {\begin{array}{*{20}{c}}{2x - y = - 3}\\{x + 3y = 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x - y = - 3}\\{2x + 6y = 8}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 7y = - 11}\\{x = 4 - 3y}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{y = \dfrac{{11}}{7}}\\{x = \dfrac{{ - 5}}{7}}\end{array}} \right.} \right.\end{array}\) Vậy hệ phương trình có nghiệm \(\left( {\dfrac{{ - 5}}{7};\,\,\dfrac{{11}}{7}} \right)\). |
2)
a) Phương trình \({x^2} - 2\left( {m + 2} \right)x + {m^2} + 7 = 0\) có: \(\Delta ' = {\left( {m + 2} \right)^2} - {m^2} - 7 = 4m - 3\).
Phương trình có 2 nghiệm phân biệt \(\Delta ' > 0 \Leftrightarrow 4m - 3 > 0 \Leftrightarrow m > \dfrac{3}{4}\).
Vậy với \(m > \dfrac{3}{4}\) thì phương trình có hai nghiệm phân biệt
b) Với\(m > \dfrac{3}{4}\), theo định lí Vi-et ta có: \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2m + 4}\\{{x_1}{x_2} = {m^2} + 7}\end{array}} \right.\)
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,{x_1}^2 + {x_2}^2 = {x_1}{x_2} + 12\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {x_1}{x_2} + 12\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2} - 12 = 0\\ \Leftrightarrow {\left( {2m + 4} \right)^2} - 3\left( {{m^2} + 7} \right) - 12 = 0\\ \Leftrightarrow 4{m^2} + 16m + 16 - 3{m^2} - 21 - 12 = 0\\ \Leftrightarrow {m^2} + 16m - 17 = 0\end{array}\)
Ta có \(a + b + c = 1 + 16 - 17 = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}m = 1\,\,\left( {tm} \right)\\m = \dfrac{c}{a} = - 17\,\,\left( {ktm} \right)\end{array} \right.\).
Vậy \(m = 1\).
Bài 3:
Phương pháp:
Đổi các đại lượng thời gian về cùng một đơn vị
Gọi vận tốc lúc lên dốc của người đó là \(x\,\,\left( {km/h} \right)\,\,\left( {x > 0} \right)\).
Lập phương trình ẩn \(x\), giải phương trình đối chiếu điều kiện và kết luận.
Cách giải:
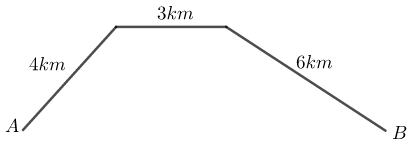
Đổi 130 phút = \(\dfrac{{13}}{6}\left( h \right)\)
Gọi vận tốc lúc lên dốc của người đó là \(x\,\,\left( {km/h} \right)\,\,\left( {x > 0} \right)\). Thì vận tốc lúc xuông dốc là \(x + 5\,\,\,\left( {km/h} \right)\).
Thời gian lúc lên dốc, xuống dốc trên quãng đường 4km lần lượt là: \(\dfrac{4}{x}\)\(\left( h \right)\) và \(\dfrac{4}{{x + 5}}\,\,\left( h \right)\).
Thời gian lúc đi trên quãng đường 3km là \(\dfrac{3}{{12}} = \dfrac{1}{4}\,\,\left( h \right)\)
Thời gian lúc lên và xuống dốc trên quãng đường 6km lần lượt là: \(\dfrac{6}{x}\left( h \right)\) và \(\dfrac{6}{{x + 5}}\left( h \right)\).
Tổng thời gian đi từ A đến B là: \(\dfrac{4}{x} + \dfrac{1}{4} + \dfrac{6}{{x + 5}}\,\,\left( h \right)\)
Tổng thời gian đi từ B đến A là: \(\dfrac{6}{x} + \dfrac{1}{4} + \dfrac{4}{{x + 5}}\,\,\,\left( h \right)\)
Tổng thời gian cả đi cả về là bằng \(\dfrac{{13}}{6}h\) nên ta có phương trình:
\(\begin{array}{l}\dfrac{4}{x} + \dfrac{1}{4} + \dfrac{6}{{x + 5}} + \dfrac{6}{x} + \dfrac{1}{4} + \dfrac{4}{{x + 5}} = \dfrac{{13}}{6}\\ \Leftrightarrow \dfrac{{10}}{x} + \dfrac{1}{2} + \dfrac{{10}}{{x + 5}} = \dfrac{{13}}{6}\\ \Leftrightarrow \dfrac{{10\left( {x + x + 5} \right)}}{{x\left( {x + 5} \right)}} = \dfrac{5}{3}\\ \Leftrightarrow \dfrac{{2x + 5}}{{x\left( {x + 5} \right)}} = \dfrac{1}{6}\\ \Rightarrow 6\left( {2x + 5} \right) = x\left( {x + 5} \right)\\ \Leftrightarrow {x^2} - 7x - 30 = 0\end{array}\)
Ta có \(\Delta = {\left( { - 7} \right)^2} - 4.\left( { - 30} \right) = 169 = {13^2} > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}x = \dfrac{{7 + 13}}{2} = 10\,\,\,\left( {tm} \right)\\x = \dfrac{{7 - 13}}{2} = - 3\,\,\left( {ktm} \right)\end{array} \right.\).
Vậy vận tốc lúc lên dốc là 10 km/h và vận tốc lúc xuống dốc là 15 km/h.
Bài 4:
Phương pháp:
a) Vận dụng dấu hiệu nhận biết tứ giác nội tiếp: chứng minh tứ giác \(SAOB\) nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)), suy ra \(S,A,O,B\) cùng thuộc một đường tròn.
b) Vận dụng tính chất đường trung trực của đoạn thẳng
Vận dụng hệ thức lượng trong tam giác vuông
c) Áp dụng kiến thức góc – đường tròn
Kiến thức về tam giác đồng dạng để suy ra các tỷ lệ cạnh tương ứng từ đó chứng minh được hệ thức của đề bài.
d) Vận dụng dấu hiệu nhận biết của hình thoi, các hệ thức lượng trong tam giác vuông.
Cách giải:
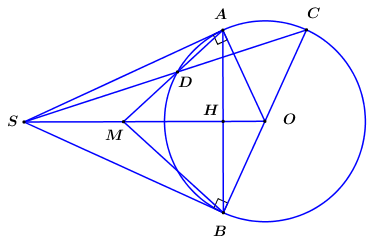
a) Tứ giác \(SAOB\) có : \(\angle SAO + \angle SBO = {90^0} + {90^0} = {180^0}\)
Suy ra tứ giác \(SAOB\) nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
Suy ra \(4\) điểm \(S,A,O,B\) cùng thuộc một đường tròn.
b) Gọi \(H\) là giao điểm giữa \(AB\) và \(SO\)
Có \(SA,SB\) là hai tiếp tuyến cắt nhau nên \(SA = SB \Rightarrow S\) thuộc trung trực của \(AB\).
\(OA = OB = R\) nên \(O\) thuộc trung trực của \(AB\).
\( \Rightarrow SO\) là trung trực của \(AB\)
\( \Rightarrow \) \(AB \bot SO\) và \(H\) là trung điểm của \(AB\).
Tam giác \(SAO\) vuông tại \(A\) nên \(SA = \sqrt {S{O^2} - O{A^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 \)
Ta giác \(SAO\) vuông tại \(A\) có: \(AH \bot SO\) nên \(AH = \dfrac{{SA.AO}}{{SO}} = \dfrac{{R\sqrt 3 .R}}{{2R}} = \dfrac{{\sqrt 3 }}{2}R\)
Vậy \(AB = 2AH = 2.\dfrac{{\sqrt 3 }}{2}R = R\sqrt 3 \).
c) Tứ giác \(SAOB\) nội tiếp (cmt) nên \(\angle ASO = \angle ABO = \angle ABC\)( hai góc nội tiếp cùng chắn cung \(AO\)).
Trong \(\left( O \right)\) có: \(\angle ADC = \angle ABC\)(hai góc nội tiếp cùng chắn cung \(AC\))
Mặt khác \(\angle SDM = \angle ADC\) (hai góc đối đỉnh)
Suy ra \(\angle ASO = \angle ACD \Rightarrow \angle MSA = \angle SDM\).
Xét \(\Delta SMD\) và \(\Delta AMS\) có: \(\left\{ \begin{array}{l}\angle SMD = \angle SMA\\\angle SDM = \angle MSA\,\,\left( {cmt} \right)\end{array} \right.\)
\( \Rightarrow \Delta SMD \sim \Delta AMS\,\,\left( {g.g} \right)\)\( \Rightarrow \dfrac{{SM}}{{AM}} = \dfrac{{MD}}{{SM}} \Rightarrow S{M^2} = MD.MA\,\,\,\left( {dpcm} \right)\).
d) Theo ý c) ta có: \(\Delta SMD \sim \Delta AMS\)\( \Rightarrow \angle MSA = \angle MDS = \angle ADC\).
Để \(OAMB\) là hình thoi thì \(\angle OAH = \angle MAH\).
Mà \(\angle OAH = \angle MSA\) (cùng phụ với \(\angle AOS\)) \( = \angle ADC\).
\( \Rightarrow \angle MAH = \angle ADC\) \( \Rightarrow cungBD = cungAC\) (2 góc nội tiếp bằng nhau thì hai cung bị chắn bằng nhau).
\( \Rightarrow AC = BD\) (2 cung bằng nhau căng hai dây bằng nhau).
Ta có: \(\angle BAC = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Leftrightarrow AB \bot AC\).
Mà \(SO\) là trung trực của \(AB\,\,\left( {cmt} \right) \Rightarrow SO \bot AB\).
\( \Rightarrow AC//SO\) (từ vuông góc đến song song) \( \Rightarrow AC//MO\).
Mà \(AM//OC\) (do \(OAMB\) là hình thoi).
\( \Rightarrow AMOC\) là hình bình hành (dhnb) \( \Rightarrow AC = OM\) (2 cạnh đối của hình bình hành).
\( \Rightarrow OM = BD\) \( \Rightarrow 2OH = BD\).
Xét tam giác \(SBC\) vuông tại \(B\), đường cao \(BD\) có: \(\dfrac{1}{{B{D^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{C^2}}}\) (hệ thức lượng trong tam giác vuông).
\(\begin{array}{l} \Rightarrow \dfrac{1}{{B{D^2}}} = \dfrac{1}{{S{O^2} - O{B^2}}} + \dfrac{1}{{4{R^2}}}\\ \Rightarrow \dfrac{1}{{2O{H^2}}} = \dfrac{1}{{{d^2} - {R^2}}} + \dfrac{1}{{4{R^2}}}\,\,\left( * \right)\end{array}\)
Xét tam giác vuông \(OAS\), đường cao \(AH\) ta có: \(OH.OS = O{A^2}\) (hệ thức lượng trong tam giác vuông).
\( \Rightarrow OH.d = {R^2} \Rightarrow OH = \dfrac{{{R^2}}}{d} \Rightarrow O{H^2} = \dfrac{{{R^4}}}{{{d^2}}}\).
Thay vào (*) ta có:
\(\begin{array}{l}\dfrac{{{d^2}}}{{2{R^4}}} = \dfrac{1}{{{d^2} - {R^2}}} + \dfrac{1}{{4{R^2}}}\\ \Leftrightarrow \dfrac{{2{d^2}\left( {{d^2} - {R^2}} \right)}}{{4{R^4}\left( {{d^2} - {R^2}} \right)}} = \dfrac{{4{R^4} + {R^2}\left( {{d^2} - {R^2}} \right)}}{{4{R^4}\left( {{d^2} - {R^2}} \right)}}\\ \Leftrightarrow 2{d^2}\left( {{d^2} - {R^2}} \right) = 4{R^4} + {R^2}{d^2} - {R^4}\\ \Leftrightarrow 2{d^4} - 2{d^2}{R^2} = 3{R^4} + {R^2}{d^2}\\ \Leftrightarrow 2{d^4} - 3{d^2}{R^2} - 3{R^4} = 0\\ \Leftrightarrow {d^2} = \dfrac{{3 + \sqrt {33} }}{4}{R^2}\\ \Leftrightarrow d = \dfrac{{\sqrt {3 + \sqrt {33} } }}{2}R\end{array}\)
Vậy để \(OAMB\) là hình thoi thì \(d = \dfrac{{\sqrt {3 + \sqrt {33} } }}{2}R\).
Bài 5:
Phương pháp:
Áp dụng BĐT Co-si cho hai số \(\sqrt {{x^2} + 3} \) và \(\dfrac{4}{{\sqrt {{x^2} + 3} }}\) để tìm giá trị nhot nhất của biểu thức.
Cách giải:
Áp dụng BĐT Co-si ta có:
\(\dfrac{{{x^2} + 7}}{{\sqrt {{x^2} + 3} }} = \dfrac{{\left( {{x^2} + 3} \right) + 4}}{{\sqrt {{x^2} + 3} }} = \sqrt {{x^2} + 3} + \dfrac{4}{{\sqrt {{x^2} + 3} }} \ge 2\sqrt {\sqrt {{x^2} + 3} .\dfrac{4}{{\sqrt {{x^2} + 3} }}} = 2\sqrt 4 = 4\)
Đặt: \(a = \dfrac{{{x^2} + 7}}{{\sqrt {{x^2} + 3} }} \ge 4 \Rightarrow \dfrac{1}{a} = \dfrac{{\sqrt {{x^2} + 3} }}{{{x^2} + 7}}\)
\(\begin{array}{l} \Rightarrow T = a + \dfrac{1}{a} = \left( {\dfrac{a}{{16}} + \dfrac{1}{a}} \right) + \dfrac{{15a}}{{16}}\\\,\,\,\,\,\,\,\,\,\,\, \ge 2.\sqrt {\dfrac{a}{{16}}.\dfrac{1}{a}} + \dfrac{{15.4}}{{16}} = \dfrac{1}{2} + \dfrac{{15}}{4} = \dfrac{{17}}{4}\end{array}\)
(Bất đẳng thức cô-si)
Dấu “=” xảy ra khi và chỉ khi:
\(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{a}{{16}} = \dfrac{1}{a}\\a = 4\end{array} \right. \Leftrightarrow a = 4 \Leftrightarrow \dfrac{{{x^2} + 7}}{{\sqrt {{x^2} + 3} }} = 4\\ \Leftrightarrow {x^2} + 7 = 4\sqrt {{x^2} + 3} \Leftrightarrow {\left( {{x^2} + 7} \right)^2} = 16\left( {{x^2} + 3} \right)\\ \Leftrightarrow {x^4} + 14{x^2} + 49 = 16{x^2} + 48\\ \Leftrightarrow {x^4} - 2{x^2} + 1 = 0\\ \Leftrightarrow {\left( {{x^2} - 1} \right)^2} = 0\\ \Leftrightarrow {x^2} = 1 \Leftrightarrow x = \pm 1\end{array}\)
Vậy \(\min T = \dfrac{{17}}{4} \Leftrightarrow x = \pm 1\).
