Đề bài
Câu 1: Đồ thị ở hình bên là đồ thị hàm số nào trong các hàm số sau:
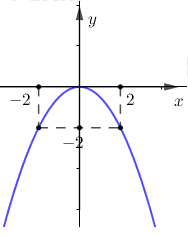
A. \(y = - 2{x^2}\)
B. \(y = - \dfrac{1}{4}{x^2}\)
C. \(y = - 4{x^2}\)
D. \(y = - \dfrac{1}{2}{x^2}\)
Câu 2. Tìm điều kiện của x để đẳng thức \(\sqrt {\dfrac{{x + 2}}{{x - 3}}} = \dfrac{{\sqrt {x + 2} }}{{\sqrt {x - 3} }}\) đúng.
A. \(x > 2\)
B. \(x \ge - 2\)
C. \(x \ge - 3\)
D. \(x > 3\)
Câu 3. Độ dài hai cạnh của một tam giác là 2 (cm) và 21 (cm). Số đo nào dưới đây có thể là độ dài cạnh thứ ba của tam giác đã cho?
A. 19 (cm)
B. 22 (cm)
C. 23(cm)
D. 24 (cm)
Câu 4. Tìm các giá trị của a sao cho \(\dfrac{{a - 1}}{{\sqrt a }} < 0.\)
A. \(a \ge 0\)
B. \(0 \le a < 1\)
C. \(a < 1\)
D. \(0 < a < 1\)
Câu 5. Cho số tự nhiên \(\overline {10203x} \) . Tìm tất cả các chữ số x thích hợp để số đã cho chia hết cho 3 mà không chia hết cho 9?
A. \(x \in \left\{ {0;6;9} \right\}\)
B. \(x \in \left\{ {0;3;6} \right\}\)
C. \(x \in \left\{ {3;6;9} \right\}\)
D. \(x \in \left\{ {0;3;9} \right\}\)
Câu 6. Biết phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có một nghiệm x = 1. Đẳng thức nào sau đây đúng ?
A. \(a - b - c = 0.\)
B. \(a + b - c = 0.\)
C. \(a + b + c = 0.\)
D. \(a - b + c = 0.\)
Câu 7. Xác định hàm số \(y = ax + b,\) biết đồ thị của hàm số đi qua hai điểm \(A\left( { - 2;5} \right)\) và \(B\left( {1; - 4} \right)\)
A. \(y = x - 3\)
B. \(y = - x - 3\)
C. \(y = - 3x - 1\)
D. \(y = 3x - 1\)
Câu 8. Trong các phân số sau, phân số nào viết dưới dạng số thập phân vô hạn tuần hoàn?
A. \(\dfrac{{17}}{{20}}.\)
B. \(\dfrac{7}{{55}}.\)
C. \(\dfrac{{19}}{{128}}.\)
D. \(\dfrac{{67}}{{625}}.\)
Câu 9.Tìm tất cả các giá trị của m để đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) nằm phía dưới trục hoành.
A. \(m < - \dfrac{1}{2}\)
B. \(m > - \dfrac{1}{2}\)
C. \(m \ge - \dfrac{1}{2}\)
D. \(m \le - \dfrac{1}{2}\)
Câu 10: Phương trình \(\dfrac{3}{{1 - 4x}} = \dfrac{2}{{4x + 1}} - \dfrac{{8 + 6x}}{{16{x^2} - 1}}\) có bao nhiêu nghiệm?
A. 2
B. 0
C. 1
D. 3
Câu 11. Đẳng thức nào sau đây đúng với mọi \(x \le 0?\)
A. \(\sqrt {9{x^2}} = 3x\)
B. \(\sqrt {9{x^2}} = - 3x\)
C. \(\sqrt {9{x^2}} = 9x\)
D. \(\sqrt {9{x^2}} = - 9x\)
Câu 12. Tìm số tự nhiên n có hai chữ số, biết rằng tổng các chữ số của nó bằng 9 và nếu cộng thêm vào số đó 63 đơn vị thì được một số mới cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại.
A. n = 36
B. n = 18
C. n = 45
D. n = 27
Câu 13. Cho \(Q = 4a - \sqrt {{a^2} - 4a + 4} ,\) với \(a \ge 2\) . Khẳng định nào sau đây đúng?
A. \(Q = 5a + 2.\)
B. \(Q = 3a - 2.\)
C. \(Q = 3a + 2.\)
D. \(Q = 5a - 2.\)
Câu 14. Biều thức \(M = {x^2} - 1\) bằng biểu thức nào sau đây?
A. \(M = \left( {1 - x} \right)\left( {x + 1} \right).\)
B. \(M = \left( {x - 1} \right)\left( {1 - x} \right).\)
C. \(M = \left( {x - 1} \right)\left( {x - 1} \right).\)
D. \(M = \left( {x - 1} \right)\left( {x + 1} \right).\)
Câu 15: Cho tam giác ABC, M thuộc cạnh AB, N thuộc cạnh BC, biết \(\dfrac{{MA}}{{MB}} = \dfrac{{NC}}{{NB}} = \dfrac{2}{5},MN = 15\left( {cm} \right).\). Tính độ dài cạnh AC.
A. AC = 21 (cm).
B. AC = 37,5 (cm)
C. AC = 52,5 (cm).
D. AC = 25 (cm).
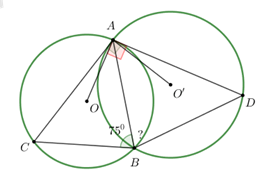
Câu 16. Cho hai đường tròn (O) và (O’) cắt nhau tại A, B. Tiếp tuyến tại A của đường tròn (O’) cắt (O) tại C và của (O) cắ (O’) tại D. Biết \(\widehat {ABC} = {75^0}\) . Tính \(\widehat {ABD}?\)
A. \(\widehat {ABD} = {40^0}.\)
B. \(\widehat {ABD} = {150^0}.\)
C. \(\widehat {ABD} = {50^0}.\)
D. \(\widehat {ABD} = {75^0}.\)
Câu 17. Số đo 3 góc của một tam giác tỉ lệ với các số 2; 3; 5. Tìm số đo của góc nhỏ nhất.
A. \({36^0}\)
B. \({18^0}\)
C. \({24^0}\)
D. \({54^0}\)
Câu 18. Trong các hình cho dưới đây, hình nào mô tả góc ở tâm?
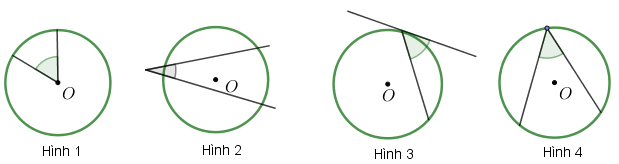
A. Hình 3 và Hình 4.
B. Hình 1.
C. Hình 2.
D. Hình 1 và Hình 4
Câu 19. Tính \(M = \dfrac{{\sqrt {12} }}{{\sqrt 3 }}\)
A. \(M = 4\)
B. \(M = 3\)
C. \(M = 1\)
D. \(M = 2\)
Câu 20. Cho \(P = \sqrt {4{a^2}} - 6a.\) Khẳng định nào sau đây đúng?
A. \(P = - 4a.\)
B. \(P = - 4\left| a \right|.\)
C. \(P = 2a - 6\left| a \right|.\)
D. \(P = 2\left| a \right| - 6a.\)
Câu 21. Tính thể tích V của hình cầu có bán kính \(R = 3\left( {cm} \right).\)
A. \(V = 108\pi \left( {c{m^3}} \right)\)
B. \(V = 9\pi \left( {c{m^3}} \right)\)
C. \(V = 72\pi \left( {c{m^3}} \right)\)
D. \(V = 36\pi \left( {c{m^3}} \right)\)
Câu 22. Cho \(P = \sqrt {{{\left( {\sqrt 3 + 1} \right)}^2}} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \) . Khẳng định nào sau đây đúng?
A. \(P = 2\)
B. \(P = 2 + 2\sqrt 3 \)
C. \(P = 2 - \sqrt 3 \)
D. \(2\sqrt 3 \)
Câu 23. Khẳng định nào sau đây sai?
A. \(\cos \,{35^0} > \sin {40^0}.\)
B. \(\sin {35^0} > \cos \,{40^0}.\)
C. \(\sin {35^0} < \sin \,{40^0}.\)
D. \(\cos \,{35^0} > \cos {40^0}.\)
Câu 24. Bạn An chơi thả diều. Tại thời điểm dây diều dài 80(m) và tạo với phương thẳng đứng một góc \({50^0}\) . Tính khoảng cách d từ diều đến mặt đất tại thời điểm đó (giả sử dây diều căng và không giãn; kết quả làm tròn đến chữ số thập phân thứ hai).
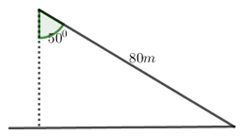
A. \(d \approx 51,42\left( m \right).\)
B. \(d \approx 57,14\left( m \right).\)
C. \(d \approx 54,36\left( m \right).\)
D. \(d \approx 61,28\left( m \right).\)
Câu 25. Tìm giá trị của m để hàm số \(y = \left( {2m - 1} \right)x + m + 2\) cắt trục hoành tại điểm có hoành độ bằng \( - \dfrac{2}{3}\) .
A. \(m = - \dfrac{1}{2}\)
B. \(m = \dfrac{1}{2}\)
C. \(m = - 8\)
D. \(m = 8\)
Câu 26: Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac < 0\). Khẳng định nào sau đây đúng?
A. Phương trình vô nghiệm.
B. Phương trình có nghiệm kép.
C. Phương trình có hai nghiệm phân biệt.
D. Phương trình có vô số nghiệm.
Câu 27. Tìm tất cả các giá trị của a, b để hệ phương trình \(\left\{ \begin{array}{l}2x + by = - 4\\bx - ay = - 5\end{array} \right.\) có nghiệm (x;y) = (1;-2)
A. \(a = 2,b = 2\)
B. \(a = - 4,b = 3\)
C. \(a = - 3,b = 4\)
D. \(a = - 4,b = - 5\)
Câu 28. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 1\\4x + y = 5\end{array} \right.\)
A. \(\left( {x;y} \right) = \left( { - 1; - 1} \right).\)
B. \(\left( {x;y} \right) = \left( { - 1;1} \right).\)
C. \(\left( {x;y} \right) = \left( {1;1} \right).\)
D. \(\left( {x;y} \right) = \left( {1; - 1} \right).\)
Câu 29. Tính bán kính r của đường tròn nội tiếp tam giác đều ABC cạnh a.
A. \(r = \dfrac{{a\sqrt 3 }}{6}.\)
B. \(r = a\sqrt 3 .\)
C. \(r = \dfrac{{a\sqrt 3 }}{3}.\)
D. \(r = \dfrac{{2a\sqrt 3 }}{3}.\)
Câu 30. Trong các số sau, số nào là số nguyên tố.
A. 29
B. 35.
C. 49.
D. 93
Câu 31. Cho một hình cầu có đường kính bằng 4 (cm). Tính diện tích S của hình cầu đó.
A. \(S = \dfrac{{16\pi }}{3}\left( {c{m^2}} \right)\) .
B. \(S = 16\pi \,\left( {c{m^2}} \right)\)
C. \(S = 64\pi \,\left( {c{m^2}} \right)\)
D. \(S = 32\pi \,\left( {c{m^2}} \right)\)
Câu 32. Trong các hàm số sau, hàm số nào đồng biến với mọi \(x \in R?\)
A. \(y = - 2x + 4.\)
B. \(y = \sqrt 3 x - 2.\)
C. \(y = - \left( {\dfrac{7}{2} + 2x} \right).\)
D. \(y = \dfrac{{1 - x}}{3}\)
Câu 33. Tìm điều kiện của m để hàm số \(y = \left( {2m - 1} \right)x + 2\) luôn đồng biến.
A. \(m \ge \dfrac{1}{2}.\)
B. \(m < \dfrac{1}{2}.\)
C. \(m > \dfrac{1}{2}.\)
D. \(m \le \dfrac{1}{2}.\)
Câu 34. Cho tứ giác ABCD có \(AB = BC = CD = DA.\) Khẳng định nào sau đây đúng?
A. Tứ giác ABCD là hình vuông.
B. Tứ giác ABCD là hình chữ nhật.
C. Tứ giác ABCD là hình thoi.
D. Tứ giác ABCD là hình thang cân.
Câu 35. Rút gọn biểu thức \(M = {\left( {x - y} \right)^2} - {\left( {x + y} \right)^2}.\)
A. \(M = - 2xy.\)
B. \(M = - 4xy.\)
C. \(M = - 2{x^2}.\)
D. \(M = - 2{y^2}.\)
Câu 36. Tính chu vi của tam giác cân ABC. Biết AB = 6(cm); AC = 12(cm).
A. 25(cm)
B. 24(cm).
C. 30 (cm).
D. 15 (cm).
Câu 37. Giải phuong trình: \({x^2} - 5x + 6 = 0.\)
A. \({x_1} = 2;{x_2} = 3.\)
B. \({x_1} = - 1;{x_2} = - 6.\)
C. \({x_1} = 1;{x_2} = 6.\)
D. \({x_1} = - 2;{x_2} = - 3.\)
Câu 38. Cho \(P = 4 + {4^2} + ... + {4^{2018}} + {4^{2019}}.\) Tìm số dư khi chia P cho 20.
A. 8.
B. 16.
C. 4.
D. 12.
Câu 39. Cho tam giác ABC vuông tại A, đường cao AH và đường trung tuyến AM \(\left( {H,M \in BC} \right)\) . Biết chu vi của tam giác là 72cm và AM – AH = 7 (cm). Tính diện tích S của tam giác ABC.
A. \(S = 48\left( {c{m^2}} \right)\)
B. \(S = 108\left( {c{m^2}} \right)\)
C. \(S = 148\left( {c{m^2}} \right)\)
D. \(S = 144\left( {c{m^2}} \right)\)
Câu 40. Cho các số a, b, c thỏa mãn \({a^2} + {b^2} + {c^2} + 6 = 2\left( {a + 2b + c} \right).\) Tính tổng \(T = a + b + c.\)
A. \(T = 6.\)
B. \(T = 2.\)
C. \(T = 4.\)
D. \(T = 8.\)
Câu 41. Cho tam giác ABC có AB = 20(cm), BC = 12 (cm), CA = 16 (cm). Tính chu vi của đường tròn nội tiếp tam giác đã cho.
A. \(16\pi \left( {cm} \right).\)
B. \(20\pi \left( {cm} \right).\)
C. \(13\pi \left( {cm} \right).\)
D. \(8\pi \left( {cm} \right).\)
Câu 42: Biết các cạnh của một tứ giác tỉ lệ với 2; 3; 4; 5 và độ dài cạnh lớn nhất hơn độ dài cạnh nhỏ nhất là 6(cm). Tính chu vi của tứ giác đó.
A. 28 (cm).
B. 42 (cm).
C. 14 (cm)
D. 56 (cm).
Câu 43: Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - m + 3 = 0\) (m là tham số). Tìm các giá trị của m để phương trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10.\)
A. \(m = 1.\)
B. \(m = 4.\)
C. \(m = - 1.\)
D. \(m = - 4.\)
Câu 44. Cho tam giác ABC, biết \(\widehat B = {60^0},AB = 6\left( {cm} \right),BC = 4\left( {cm} \right).\) Tính độ dài của cạnh AC.
A. \(AC = 2\sqrt 7 \left( {cm} \right).\)
B. \(AC = \sqrt {52} \left( {cm} \right).\)
C. \(AC = 4\sqrt 5 \left( {cm} \right).\)
D. \(AC = 2\sqrt 3 \left( {cm} \right).\)
Câu 45. Mặt cầu (S) được gọi là ngoại tiếp hình lập phương ABCD.A’B’C’D’ nếu các đỉnh của hình laapoj phương đều thuộc mặt cầu (S). Biết hình lập phương có độ dài cạnh 2a, tính thể tích V của hình cầu ngoại tiếp hình lập phương đó.
A. \(V = 3\pi {a^3}.\)
B. \(V = 4\sqrt 3 \pi {a^3}.\)
C. \(V = \dfrac{{\sqrt 3 }}{2}\pi {a^3}.\)
D. \(V = 3\sqrt 2 \pi {a^3}.\)
Câu 46. Cho \(\widehat {xOy} = {45^0}.\) Trên tia Oy lấy hai điểm A, B sao cho \(AB = \sqrt 2 \left( {cm} \right).\) Tính độ dài hình chiếu vuông góc của đoạn thẳng AB trên Ox.
A. \(\dfrac{{\sqrt 2 }}{2}\left( {cm} \right).\)
B. \(\dfrac{{\sqrt 2 }}{4}\left( {cm} \right).\)
C. \(1\left( {cm} \right).\)
D. \(\dfrac{1}{2}\left( {cm} \right).\)
Câu 47: Một tấm tôn hình chữ nhật có chu vi là 48 cm. Người ta cắt bỏ mỗi góc của tấm tôn một hình vuông có cạnh 2cm rồi gấp lên thành một hình hộp chữ nhật không nắp có thể tích \(96c{m^3}.\) Giả sử tấm tôn có chiều dài là a, chiều rộng là b. Tính giá trị biểu thức \(P = {a^2} - {b^2}.\)
A. P = 80 B. P = 112.
C. P = 192. D. P = 256.
Câu 48. Hai vòi nước cùng chảy vào một bể không có nước. Nếu cho vòi một chảy trong 3 giờ rồi hóa lại, sau đó cho vòi hai chảy tiếp trong 8 giờ nữa thì đầy bể. Nếu cho vòi một chảy trong 1 giờ, rồi cho cả hai vòi chảy tiếp trong 4 giờ nữa thì số nước chảy vào bằng \(\dfrac{8}{9}\) bể. Hỏi nếu chảy một mình thì vòi một sẽ chảy trong thời gian t bằng bao nhiêu thì đầy bể?
A. t = 10 giờ. B. t = 12 giờ.
C. t = 11 giờ. D. t = 9 giờ.
Câu 49. Kết quả rút gọn biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\) với \(x \ge 0,x \ne 4\) có dạng \(\dfrac{{\sqrt x - m}}{{\sqrt x + n}}.\) Tính giá trị của m – n.
A. \(m - n = - 2.\)
B. \(m - n = - 4.\)
C. \(m - n = 4.\)
D. \(m - n = 2.\)
Câu 50. Cho hình vuông ABCD cạnh bằng a. Gọi E là trung điểm của CD. Tính độ dài dây cung chung CF của đường tròn đường kính BE và đường tròn đường kính CD.
A. \(CF = a.\)
B. \(CF = \dfrac{{2a\sqrt 5 }}{5}.\)
C. \(CF = \dfrac{{2a\sqrt 3 }}{3}.\)
D. \(CF = \dfrac{{a\sqrt 5 }}{5}.\)
Lời giải chi tiết
|
1.D |
11.B |
21.D |
31.B |
41.D |
|
2.D |
12.B |
22.D |
32.B |
42.A |
|
3.B |
13.C |
23.B |
33.C |
43.A |
|
4.D |
14.D |
24.A |
34.C |
44.A |
|
5.C |
15.A |
25.D |
35.B |
45.C |
|
6.C |
16.D |
26.A |
36.C |
46.C |
|
7.C |
17.A |
27.B |
37.A |
47.C |
|
8.B |
18.B |
28.C |
38 |
48.D |
|
9.A |
19.D |
29.C |
39.D |
49.D |
|
10.C |
20.D |
30.A |
40.C |
50 |
Câu 1.
Giả sử hàm số có dạng: \(y = a{x^2}\) . Ta có điểm \(\left( {2; - 2} \right)\) thuộc đồ thị đã cho nên: \( - 2 = a{.2^2} \Rightarrow a = \dfrac{{ - 1}}{2}\)
Vậy hàm số cần tìm là: \(y = - \dfrac{1}{2}{x^2}\)
Chọn D.
Câu 2.
Điều kiện để : \(\sqrt {\dfrac{{x + 2}}{{x - 3}}} = \dfrac{{\sqrt {x + 2} }}{{\sqrt {x - 3} }}\)đúng \( \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\x - 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x > 3\end{array} \right.\) \( \Leftrightarrow x > 3\)
Chọn D.
Câu 3.
Gọi độ dài cạnh cần tìm của tam giác là a (cm)
Theo mối liên hệ giữa các cạnh trong một tam giác ta có a phải thỏa mãn đồng thời các điều kiện sau:
\(\left\{ \begin{array}{l}a + 2 > 21\\2 + 21 > a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a > 19\\a < 23\end{array} \right.\)
Vậy dựa vào các đáp án của đầu bài thì a = 22 (cm)
Chọn B.
Câu 4.
\(\dfrac{{a - 1}}{{\sqrt a }} < 0 \Leftrightarrow \left\{ \begin{array}{l}a - 1 < 0\\a > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 1\\a > 0\end{array} \right.\)
Chọn D.
Câu 5.
Ta có số tự nhiên : \(\overline {10203x} \vdots 3 \Leftrightarrow 1 + 0 + 2 + 0 + 3 + x \vdots 3\) \( \Leftrightarrow 6 + x \vdots 3\)
Khi đó x có thể nhận các giá trị \(\left\{ {0;3;6;9} \right\}\)
Mà số \(\overline {10203x} \) không chia hết cho 9 nên x = 3 không thỏa mãn.
Vậy \(x \in \left\{ {0;6;9} \right\}\)
Chọn C.
Câu 6.
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có \(a + b + c = 0\) thì phương trình luôn có nghiệm \(x = 1\) và nghiệm còn lại là \(x = \dfrac{c}{a}\) .
Chọn C.
Câu 7.
Đồ thị của hàm số \(y = ax + b,\)đi qua hai điểm \(A\left( { - 2;5} \right)\) và \(B\left( {1; - 4} \right)\) nên ta có: \(\left\{ \begin{array}{l} - 2a + b = 5\\a + b = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3a = 9\\b = - 4 - a\end{array} \right. \) \(\Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = - 1\end{array} \right.\)
Vậy hàm số cần tìm là: \(y = - 3x - 1\)
Chọn C.
Câu 8:
Ta có: \(20 = {2^2}.5,\;\;55 = 5.11,\;\;128 = {2^7},\)\(\;\;625 = {5^4}.\)
Chỉ có mẫu số 55 là có ước nguyên tố 11 khác 2 và 5 nên phân số \(\dfrac{7}{{55}}.\)có thể viết được dưới dạng số thập phân vô hạn tuần hoàn.
Chọn B.
Câu 9.
Đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) nằm phía dưới trục hoành tức là \(y < 0 \Leftrightarrow 2m + 1 < 0\)
\(\Leftrightarrow m < - \dfrac{1}{2}\,\,\left( {Do\,\,\,{x^2} \ge 0} \right)\)
Chọn A.
Câu 10:
Điều kiện: \(x \ne \pm \dfrac{1}{4}\)
\(\begin{array}{l}\dfrac{3}{{1 - 4x}} = \dfrac{2}{{4x + 1}} - \dfrac{{8 + 6x}}{{16{x^2} - 1}}\\ \Leftrightarrow - 3\left( {4x + 1} \right) = 2\left( {4x - 1} \right) - 8 - 6x\\ \Leftrightarrow - 12x - 3 = 8x - 2 - 8 - 6x\\ \Leftrightarrow - 14x = - 7 \Leftrightarrow x = \dfrac{1}{2}\left( {tm} \right)\end{array}\)
Vậy phương trình đã cho có 1 nghiệm.
Chọn C.
Câu 11.
Ta có: \(\sqrt {9{x^2}} = \sqrt {{{\left( {3x} \right)}^2}} = \left| {3x} \right| = - 3x\,\left( {Do\,\,x < 0} \right)\)
Chọn B.
Câu 12.
Gọi số tự nhiên n có hai chữ số là: \(\overline {ab} \,\,\left( {a \ne 0,a,b \in N} \right)\)
Tổng các chữ số của nó bằng 9 nên ta có: \(a + b = 9\,\,\left( 1 \right)\)
Nếu thêm vào số đó 63 đơn vị thì được một số mới cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại. Nên ta có phương trình:
\(\begin{array}{l}\;\;\;\;\overline {ab} + 63 = \overline {ba} \Leftrightarrow 10a + b + 63 = 10b + a\\ \Leftrightarrow 9a - 9b = - 63 \Leftrightarrow a - b = - 7\,\,\;\;\left( 2 \right)\end{array}\)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}a + b = 9\\a - b = - 7\end{array} \right.\left\{ \begin{array}{l}a = 1\\b = 8\end{array} \right. \Rightarrow \overline {ab} = 18\)
Vậy số cần tìm là: n = 18.
Chọn B.
Câu 13.
\(Q = 4a - \sqrt {{a^2} - 4a + 4}\)\(\, = 4a - \sqrt {{{\left( {a - 2} \right)}^2}} \)\(\,= 4a - \left| {a - 2} \right| = 4a - \left( {a - 2} \right)\)\(\, = 3a + 2\left( {do\,\,a \ge 2} \right)\)
Chọn C.
Câu 14.
\(M = {x^2} - 1 = {x^2} - {1^2} = \left( {x - 1} \right)\left( {x + 1} \right)\)
Chọn D.
Câu 15
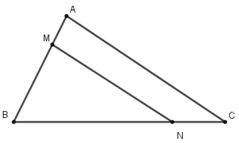
Ta có: \(\dfrac{{MA}}{{MB}} = \dfrac{{NC}}{{NB}} = \dfrac{2}{5} \Rightarrow MN\parallel AC\)
\(\dfrac{{MA}}{{MB}} = \dfrac{2}{5},MA + MB = AB\)
\(\Rightarrow \dfrac{{MA}}{{AB}} = \dfrac{2}{7};\dfrac{{MB}}{{AB}} = \dfrac{5}{7}\)
Áp dụng định lý Talet trong tam giác ABC với MN//AC ta có:
\(\dfrac{{MB}}{{AB}} = \dfrac{{MN}}{{AC}} = \dfrac{5}{7}\)
\(\Rightarrow AC = \dfrac{{7MN}}{5} = \dfrac{{7.15}}{5} = 21\left( {cm} \right)\)
Chọn A.
Câu 16.
Xét tam giác ABC và tam giác DBA có:
\(\widehat {CAB} = \widehat {ADB}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung của
đường tròn (O’) cùng chắn cung AB)
\(\widehat {ACB} = \widehat {BAD}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung của
đường tròn (O) cùng chắn cung AB)
Vậy \(\Delta ABC \sim \Delta DBA\) (g-g)
Khi đó ta có: \(\widehat {ABC} = \widehat {ABD} = {75^0}\)(2 góc tương ứng)
Chọn D.
Câu 17.
Gọi các góc của tam giác lần lượt có số đo là: x, y, z (độ) giả sử: x < y < z
Ta có: 3 góc của tam giác tỉ lệ với các số: 2; 3; 5 nên ta có: \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5}\)
Áp dụng tính chất của dãy tỷ số bằng nhau ta có: \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{5} = \dfrac{{x + y + z}}{{10}} = \dfrac{{180}}{{10}} = 18\)
Từ đó ta có: \(\dfrac{x}{2} = 18 \Rightarrow x = 36\)
Vậy góc nhỏ nhất của tam giác có số đo là: \({36^0}\) .
Chọn A.
Câu 18.
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn. Hai cạnh của góc ở tâm cắt đường tròn ở hai điểm, hai điểm này chia đường tròn thành hai cung.
Chọn B.
Câu 19.
\(M = \dfrac{{\sqrt {12} }}{{\sqrt 3 }} = \sqrt {\dfrac{{12}}{3}} = \sqrt 4 = 2\)
Chọn D
Câu 20.
\(P = \sqrt {4{a^2}} - 6a = \sqrt {{{\left( {2a} \right)}^2}} - 6a = \left| {2a} \right| - 6a = 2\left| a \right| - 6a.\)
Chọn D.
Câu 21.
Áp dụng công thức tính thể tích hình cầu ta có: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\)
Chọn D.
Câu 22.
\(P = \sqrt {{{\left( {\sqrt 3 + 1} \right)}^2}} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \)
\(\;\;\;= \left| {\sqrt 3 + 1} \right| + \left| {1 - \sqrt 3 } \right| \)
\(\;\;\;= \sqrt 3 + 1 + \sqrt 3 - 1 = 2\sqrt 3 \) \(\left( {do\,\,\sqrt 3 + 1 > 0;\,1 - \sqrt 3 < 0} \right)\)
Chọn D.
Câu 23.
Sử dụng máy tính bỏ túi để làm bài toán ta thấy đáp án B sai.
Chọn B.
Câu 24.
Ta có: \(\cos {50^0} = \dfrac{d}{{80}} \Rightarrow d \approx 51,42\left( m \right)\)
Chọn A.
Câu 25.
Đồ thị hàm số \(y = \left( {2m - 1} \right)x + m + 2\) cắt trục hoành tại điểm có hoành độ bằng \( - \dfrac{2}{3}\) . Tức là điểm \(\left( { - \dfrac{2}{3};0} \right)\) thuộc vào đồ thị hàm số.
Khi đó ta có: \(0 = \left( {2m - 1} \right).\left( { - \dfrac{2}{3}} \right) + m + 2 \) \(\Leftrightarrow m = 8\).
Chọn D.
Câu 26.
Do phương trình bậc hai có \(\Delta < 0\)nên phương trình vô nghiệm.
Chọn A.
Câu 27.
Thay \(x = 1;y = - 2\) vào hệ phương trình ta được: \(\left\{ \begin{array}{l}2.1 + b.\left( { - 2} \right) = - 4\\b.1 - a.\left( { - 2} \right) = - 5\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l} - 2b = - 6\\b + 2a = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\a = - 4\end{array} \right.\)
Vậy chọn B.
Câu 28.
\(\left\{ \begin{array}{l}2x - y = 1\\4x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x = 6\\y = 2x - 1\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\)
Vậy hệ phương trình đã cho có nghiệm là: \(\left( {x;y} \right) = \left( {1;1} \right).\)
Chọn C.
Câu 29.
Ta có đường trung tuyến trong tam giác đều cạnh a có độ dài là: \(\dfrac{{a\sqrt 3 }}{2}\) ‘
Khi đó bán kính r của đường tròn nội tiếp tam giác đều ABC là: \(\dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Chọn C.
Câu 30:
Ta có số 29 chỉ có ước là 1 và chính nó nên số 29 là số nguyên tố.
Chọn A.
Câu 31.
Ta có: hình cầu có đường kính bằng 4(cm) nên bán kính bằng 2 (cm)
Khi đó ta có diện tích S của hình cầu là: \(S = 4\pi {2^2} = 16\pi \left( {c{m^2}} \right)\)
Chọn B.
Câu 32.
Xét các đáp án ta thấy hàm số \(y = \sqrt 3 x - 2.\) có hệ số \(a = \sqrt 3 > 0\) . Nên hàm số này đồng biến với mọi \(x \in R.\)
Chọn B.
Câu 33.
Hàm số \(y = \left( {2m - 1} \right)x + 2\) luôn đồng biến khi \(2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}.\)
Chọn C.
Câu 34.
Chọn C.
Câu 35.
\(M = {\left( {x - y} \right)^2} - {\left( {x + y} \right)^2} \)\(\,= \left( {x - y + x + y} \right)\left( {x - y - x - y} \right) \)\(\,= - 4xy.\)
Chọn B.
Câu 36.
Ta có tam giác ABC cân mà đầu bài cho AB = 6(cm); AC = 12(cm) nên tam giác đó không thể cân tại A mà chỉ có thể cân tại B hoặc C,
TH1: giả sử tam giác cân tại B thì ta có BA = BC = 6 (cm). Mà theo mối quan hệ giữa các cạnh trong tam giác ta có: BA + BC > AC tức là: 6 + 6 > 12 (vô lý). Vậy tam giác ABC không thể cân tại B.
TH2: Khi đó ta có tam giác ABC cân tại C tức là: CA = CB = 12(cm).
Khi đó chu vi của tam giác ABC là: 12 + 12 + 6 = 30 (cm).
Chọn C.
Câu 37.
Ta có: \(\Delta = {b^2} - 4ac = 25 - 24 = 1 > 0\) Khi đó phương trình đã cho có hai nghiệm: \({x_1} = \dfrac{{5 - 1}}{2} = 2;{x_2} = \dfrac{{5 + 1}}{2} = 3\)
Chọn A.
Câu 39.
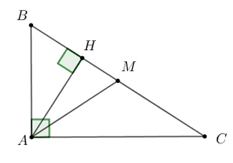
Đặt AH = a (a > 0 ) khi đó ta có: AM = a + 7 (cm).
Lại có tam giác ABC vuông tại A, có trung tuyến AM nên BC = 2AM
\( \Rightarrow BC = 2\left( {a + 7} \right)\)
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: \(AB.AC = AH.BC = 2a.\left( {a + 7} \right) = 2{a^2} + 14a.\,\,\left( 1 \right)\)
Chu vi của tam giác bằng 72 nên ta có: \(AB + AC + BC = 72 \Rightarrow AB + AC = 72 - 2\left( {a + 7} \right)\)
Áp dụng định lý Py – ta – go trong tam giác vuông ABC ta có: \(A{B^2} + A{C^2} = B{C^2} = 4{\left( {a + 7} \right)^2}\)
\(\begin{array}{l} \Rightarrow 2AB.AC = {\left( {AB + AC} \right)^2} - \left( {A{B^2} + A{C^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {\left[ {72 - 2\left( {a + 7} \right)} \right]^2} - 4{\left( {a + 7} \right)^2}\\ \Leftrightarrow 2AB.AC = 4{\left( {29 - a} \right)^2} - 4{\left( {a + 7} \right)^2}\\ \Leftrightarrow AB.AC = 2\left( {841 - 58a + {a^2}} \right) - 2\left( {{a^2} + 14a + 49} \right)\\ \Leftrightarrow AB.AC = 1584 - 144a\,\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) ta có phương trình
\(2{a^2} + 14a = 1584 - 144a \Leftrightarrow {a^2} + 79a - 792 = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}a = 9\left( {tm} \right)\\a = - 88\left( {ktm} \right)\end{array} \right.\)
Vậy AH = 9 (cm); BC = 2(9 + 7) = 32 (cm). Khi đó diện tích của tam giác ABC là: \(S = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.9.32 = 144\left( {c{m^2}} \right).\)
Chọn D.
Câu 40.
Ta có:
\(\begin{array}{l}{a^2} + {b^2} + {c^2} + 6 = 2\left( {a + 2b + c} \right)\\ \Leftrightarrow {a^2} - 2a + 1 + {b^2} - 4b + 4 + {c^2} - 2c + 1 = 0\\ \Leftrightarrow {\left( {a - 1} \right)^2} + {\left( {b - 2} \right)^2} + {\left( {c - 1} \right)^2} = 0\\ \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\b - 2 = 0\\c - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 1\end{array} \right.\end{array}\)
Nên \(T = a + b + c = 1 + 2 + 1 = 4.\)
Chọn C.
Câu 41.
Ta có: \(p = \dfrac{{20 + 12 + 16}}{2} = 24\)
Ta có: \(S = pr \)
\(\Rightarrow r = \dfrac{S}{p} = \dfrac{{\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} }}{p} \)\(\,= \dfrac{{\sqrt {24.\left( {24 - 20} \right).\left( {24 - 12} \right).\left( {24 - 16} \right)} }}{{24}} \)\(\,= \dfrac{{96}}{{24}} = 4\)
Khi đó chu vi đường tròn nội tiếp tam giác ABC là: \(C = 2\pi r = 2\pi .4 = 8\pi \) (cm).
Chọn D.
Câu 42.
Gọi các cạnh của một tứ giác lần lượt là: \(x,y,z,t\left( {0 < x < y < z < t} \right)\)
Các cạnh của một tứ giác tỉ lệ với 2; 3; 4; 5 nên ta có: \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{4} = \dfrac{t}{5}\)
Độ dài cạnh lớn nhất hơn độ dài cạnh nhỏ nhất là 6(cm) nên ta có: \(t - x = 6\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{4} = \dfrac{t}{5} = \dfrac{{t - x}}{{5 - 2}} = \dfrac{6}{3} = 2\)
\(\begin{array}{l}\dfrac{x}{2} = 2 \Rightarrow x = 4\left( {cm} \right)\\\dfrac{y}{3} = 2 \Rightarrow x = 6\left( {cm} \right)\\\dfrac{z}{4} = 2 \Rightarrow z = 8\left( {cm} \right)\\\dfrac{t}{5} = 2 \Rightarrow t = 10\left( {cm} \right)\end{array}\)
Khi đó chu vi của tứ giác là: \(4 + 6 + 8 + 10 = 28\left( {cm} \right).\)
Chọn A.
Câu 43.
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi \(\Delta ' > 0 \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} + m - 3 > 0 \Leftrightarrow m > \dfrac{2}{3}\)
Áp dụng hệ thức Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\\{x_1}.{x_2} = {m^2} - m + 3\end{array} \right.\)
Theo đề bài ta có: \(x_1^2 + x_2^2 = 10\)
\(\Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\)
\(\Leftrightarrow 4{\left( {m + 1} \right)^2} - 2\left( {{m^2} - m + 3} \right) = 10\)
\(\Leftrightarrow 2{m^2} + 10m - 12 = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}m = 1\left( {tm} \right)\\m = - 6\left( {ktm} \right)\end{array} \right.\)
Chọn A.
Câu 44.

Từ A kẻ \(AH \bot BC\) khi đó trong tam giác ABH ta có:
\(AH = AB.\sin B = 6.\sin 60 = 3\sqrt 3 \,\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác ABH ta có:
\(B{H^2} = A{B^2} - A{H^2} = {6^2} - {\left( {3\sqrt 3 } \right)^2} = 9\)
\(\Rightarrow BH = 3\left( {cm} \right)\)
Khi đó ta có: \(CH = BC - BH = 4 - 3 = 1\left( {cm} \right)\)
Áp dụng định lý Pytago trong tam giác vuông ACH ta có: \(A{C^2} = A{H^2} + H{C^2} = {\left( {3\sqrt 3 } \right)^2} + 1 = 28 \)
\(\Rightarrow AC = 2\sqrt 7 \left( {cm} \right)\)
Chọn A.
Câu 45.

Hình lập phương ABCD.A’B’C’D’ với I là tâm của hình lập
phương suy ra I chính là tâm của mặt cầu (S). I là trung điểm của A’C.
Từ đó ta có: \(R = IC = \dfrac{{A'C}}{2} = \dfrac{{\sqrt {AA{'^2} + A{C^2}} }}{2}\)\(\, = \dfrac{{\sqrt {AA{'^2} + A{B^2} + B{C^2}} }}{2} \)\(\,= \dfrac{{\sqrt {{a^2} + {a^2} + {a^2}} }}{2} = \dfrac{{a\sqrt 3 }}{2}\)
Vậy \({V_{mc}} = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}.\pi .{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)^3} = \dfrac{4}{3}\pi \dfrac{{3\sqrt 3 {a^3}}}{8} = \dfrac{{\sqrt 3 \pi {a^3}}}{2}\)
Chọn C.
Câu 46.
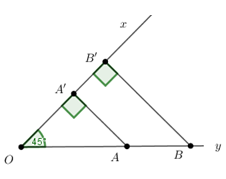
Đặt \(OA' = a,\;\;OB' = b.\)
Ta có \(\Delta OA'A\) vuông cân tại \(A' \Rightarrow OA' = AA' = a \Rightarrow OA = a\sqrt 2 .\)
\(\Delta OBB'\) vuông cân tại \(B' \Rightarrow OB' = BB' = b \Rightarrow OB = b\sqrt 2 .\)
Theo đề bài ta có: \(AB = \sqrt 2 \Rightarrow OB = OA + \sqrt 2 \Leftrightarrow b\sqrt 2 = a\sqrt 2 + \sqrt 2 \)
\( \Leftrightarrow b - a = 1 \Leftrightarrow OB' - OA' = 1 \Leftrightarrow A'B' = 1.\)
Chọn C.
Câu 47
Nửa chu vi của hình chữ nhật là: \(a + b = \dfrac{{48}}{2} = 24 \Rightarrow b = 24 - a\)
Chiều dài của mặt đáy hình chữ nhật là: \(a - 4\left( {cm} \right).\)
Chiều rộng của mặt đáy hình chữ nhật là: \(24 - a - 4 = 20 - a\left( {cm} \right).\)
Ta cần có điều kiện: \(\left\{ \begin{array}{l}a - 4 > 0\\24 - a > 0\\20 - a > 0\\24 - a \le a\end{array} \right. \Leftrightarrow 12 \le a < 24\)
Theo bài ra, ta có phương trình:
\(2.\left( {a - 4} \right).\left( {20 - a} \right) = 96 \)
\(\Leftrightarrow 20a - {a^2} - 80 + 4a = 48\)
\(\Leftrightarrow {a^2} - 24a + 128 = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}a = 16\left( {tm} \right)\\a = 8\left( {ktm} \right)\end{array} \right.\)
Khi đó ta có chiều dài là 16 (cm), chiều rộng là 24 – 16= 8 (cm) . Nên \(P = {a^2} - {b^2} = {16^2} - {8^2} = 192.\)
Chọn C.
Câu 48.
Gọi thời gian chảy một mình đầy bể của vòi 1 là: x (giờ) (x>3)
Thời gian chảy một mình đầy bể của vòi 2 là: y (giờ) (y > 8)
Mỗi giờ vòi 1 sẽ chảy được: \(\dfrac{1}{x}\) (bể)
Mỗi giờ vỏi 2 sẽ chảy được: \(\dfrac{1}{y}\) (bể)
Theo bài ra ta có: \(\dfrac{3}{x} + \dfrac{8}{y} = 1\left( 1 \right)\)
Vòi 1 chảy được 5 giờ, vòi 2 chảy được 4 giờ sẽ được \(\dfrac{8}{9}\) bể nên ta có phương trình: \(\dfrac{5}{x} + \dfrac{4}{y} = \dfrac{8}{9}\left( 2 \right)\)
Từ (1) và (2) giải hệ phương trình ta tìm được x = 9; y = 12 (giờ)
Chọn D.
Câu 49.
với \(x \ge 0,x \ne 4\)
\(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x - 2}} + \dfrac{1}{{\sqrt x + 2}}\)
\(\;\;\;= \dfrac{{x + \sqrt x + 2 + \sqrt x - 2}}{{x - 4}} \)
\(\;\;\;= \dfrac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} \)
\(\;\;\;= \dfrac{{\sqrt x }}{{\sqrt x - 2}}\)
Vậy \(m = 0;n = - 2 \Rightarrow m - n = 2\)
Chọn D.
Câu 50.
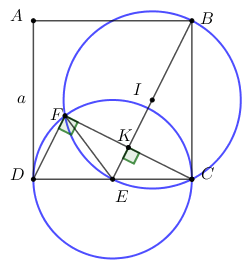
Đặt \(BI = R,\;\;CE = r,\;\;KC = x\;\;\left( {0 < x < a} \right).\)
\(\begin{array}{l}BE = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \sqrt {\dfrac{{5{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2} \Rightarrow BI = IE = \dfrac{{a\sqrt 5 }}{4} = R.\\CE = \dfrac{a}{2} = r,\;\;KE = \sqrt {C{E^2} - K{C^2}} = \sqrt {{r^2} - {x^2}} .\\KI = \sqrt {I{C^2} - K{C^2}} = \sqrt {{R^2} - {x^2}} .\\ \Rightarrow IE = KE + KI\\ \Leftrightarrow R = \sqrt {{R^2} - {x^2}} + \sqrt {{r^2} - {x^2}} \\ \Leftrightarrow {R^2} = {R^2} + {r^2} - 2{x^2} + 2\sqrt {\left( {{R^2} - {x^2}} \right)\left( {{r^2} - {x^2}} \right)} \\ \Leftrightarrow 2{x^2} - {r^2} = 2\sqrt {{R^2}{r^2} - \left( {{R^2} + {r^2}} \right){x^2} + {x^4}} \\ \Leftrightarrow 4{x^4} - 4{r^2}{x^2} + {r^4} = 4{R^2}{r^2} - 4\left( {{R^2} + {r^2}} \right){x^2} + 4{x^4}\;\;\;\left( {2{x^2} \ge {r^2}} \right)\\ \Leftrightarrow 4\left( {{R^2} + {r^2}} \right){x^2} - 4{r^2}{x^2} = 4{R^2}{r^2} - {r^4}\\ \Leftrightarrow 4{R^2}{x^2} = 4{R^2}{r^2} - {r^4}\\ \Leftrightarrow {x^2} = \dfrac{{4{R^2}{r^2} - {r^4}}}{{4{R^2}}} = \dfrac{{4.\dfrac{{5{a^2}}}{{16}}.\dfrac{{{a^2}}}{4} - \dfrac{{{a^4}}}{{16}}}}{{4.\dfrac{{5{a^2}}}{{16}}}} = \dfrac{{{a^2}}}{5}\\ \Rightarrow KC = x = \dfrac{{a\sqrt 5 }}{5} \Rightarrow FC = 2x = \dfrac{{2a\sqrt 5 }}{5}.\end{array}\)
Chọn B
soanvan.me
