Đề bài
Câu 1 (2 điểm):
a) Tính giá trị của biểu thức \(A = \sqrt {16} + \sqrt {25} .\)
b) Cho \(x \ge - 1,\,x \ne 0,\) rút gọn biểu thức \(B = \dfrac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{x}.\)
Câu 2 (1 điểm):
Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\3x + y = 1\end{array} \right..\)
Câu 3 (2 điểm):
a) Vẽ đồ thị của hàm sô \(y = x - 2.\)
b) Xác định hệ số \(a\) để đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {2;\,\,1} \right).\)
Câu 4 (1,0 điểm)
Biết rằng phương trình \({x^2} - x - 3 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\). Tính giá trị của biểu thức \(C = x_1^2 + x_2^2\).
Câu 5 (1,0 điểm)
Theo kế hoạch, một tổ trong xưởng may phải may xong 8400 chiếc khẩu trang trong một thời gian quy định. Do tình hình dịch bệnh Covid-19 diễn biến phức tạp, tổ đã quyết định tăng năng suất nên mỗi ngày tổ đã may được nhiều hơn 102 chiếc khẩu trang so với số khẩu trang phải may trong một ngày theo kế hoạch. Vì vậy, trước thời gian quy định 4 ngày, tổ đã may được 6416 chiếc khẩu trang. Hỏi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là bao nhiêu?
Câu 6 (1,0 điểm)
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\). Biết \(AB = 3cm,\,\,AC = 4cm\). Tính độ dài \(BC\) và đường cao \(AH\).
Câu 7 (2,0 điểm):
Cho đường tròn \(\left( O \right)\). Từ một điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\), kẻ hai tiếp tuyến \(MA,MB\) với đường tròn \(\left( O \right)\) (\(A,B\) là các tiếp điểm).
a) Chứng minh \(MAOB\) nội tiếp.
b) Vẽ đường kính \(BK\) của đường tròn \(\left( O \right)\), \(H\) là điểm trên \(BK\) sao cho \(AH\) vuông góc với \(BK\). Điểm \(I\) là giao điểm của \(AH,\,MK\). Chứng minh \(I\) là trung điểm \(HA\).
Lời giải
Câu 1:
Phương pháp:
a) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
b) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\) để rút gọn tử thức
Vận dụng \({\left( {\sqrt A } \right)^2} = A\,\,\,\,\left( {A \ge 0} \right)\)
Cách giải:
a) \(A = \sqrt {16} + \sqrt {25} \)
\(\begin{array}{l}\,\,\,\,\, = \sqrt {{4^2}} + \sqrt {{5^2}} \\\,\,\,\,\, = 4 + 5 = 9.\end{array}\)
Vậy \(A = 9.\)
b) Điều kiện: \(x \ge - 1,\,\,x \ne 0.\)
\(\begin{array}{l}B = \dfrac{{\left( {\sqrt {x + 1} - 1} \right)\left( {\sqrt {x + 1} + 1} \right)}}{x}\\\,\,\,\,\,\, = \dfrac{{{{\left( {\sqrt {x + 1} } \right)}^2} - 1}}{x}\\\,\,\,\,\,\, = \dfrac{{x + 1 - 1}}{x} = 1.\end{array}\)
Vậy với \(x \ge - 1,\,\,x \ne 0\) thì \(B = 1.\)
Câu 2:
Phương pháp:
Sử dụng phương pháp cộng đại số, tìm được nghiệm \(x\)
Sử dụng phương pháp thế, tìm được nghiệm \(y\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
Cách giải:
\(\left\{ \begin{array}{l}x - y = 3\\3x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 4\\y = x - 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm duy nhất \(S = \left\{ {\left( {1; - 2} \right)} \right\}.\)
Câu 3:
Phương pháp:
a) Vẽ đồ thị của hàm số \(y = ax + b\)
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
b) Thay tọa độ của điểm \(M\left( {2;\,\,1} \right)\) vào hàm số \(y = a{x^2}\), từ đó tìm được \(a\)
Cách giải:
a) Ta có bảng giá trị:
|
\(x\) |
\(0\) |
\(2\) |
|
\(y\) |
\( - 2\) |
\(0\) |
Vậy đồ thị hàm số \(y = x - 2\) là đường thẳng đi qua các điểm \(\left( {0;\, - 2} \right)\) và \(\left( {2;\,\,0} \right).\)
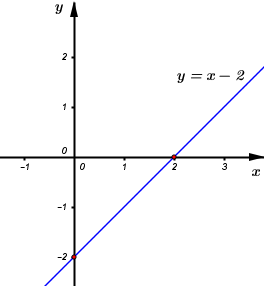
b) Đồ thị hàm số \(y = a{x^2}\) đi qua điểm \(M\left( {2;\,\,1} \right)\) \( \Leftrightarrow 1 = a{.2^2}\)\( \Leftrightarrow a = \dfrac{1}{4}\)
Vậy \(a = \dfrac{1}{4}\) thỏa mãn bài toán.
Câu 4
Phương pháp:
Chứng minh phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\)
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\)
Chú ý: \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\)
Cách giải:
Phương trình \({x^2} - x - 3 = 0\) có \(ac = - 3 < 0\) nên phương trình có hai nghiệm phân biệt trái dấu \({x_1},\,\,{x_2}\).
Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = - 3\end{array} \right.\).
Ta có: \(C = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {1^2} - 2.\left( { - 3} \right) = 7\).
Vậy \(C = 7\).
Câu 5
Phương pháp:
Gọi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(x\) (chiếc) (ĐK: \(x \in {\mathbb{N}^*}\)).
Tính được thời gian theo kế hoạch may xong số khẩu trang
Tính được thời gian theo thực tế may xong số khẩu trang
Lập được phương trình dựa vào thời gian của kế hoạch và thực tế
Giải phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Gọi số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(x\) (chiếc) (ĐK: \(x \in {\mathbb{N}^*}\)).
Vì xưởng phải may 8400 chiếc khẩu trang nên thời gian để may xong là \(\dfrac{{8400}}{x}\) (ngày).
Vì sau khi tăng năng suất nên mỗi ngày tổ đã may được nhiều hơn 102 chiếc khẩu trang so với số khẩu trang phải may trong một ngày theo kế hoạch nên thực tế mỗi ngày tổ may được \(x + 102\) (chiếc).
Thời gian tổ may được 6416 chiếc khẩu trang theo thực tế là: \(\dfrac{{6416}}{{x + 102}}\) (ngày).
Vì tổ may trước thời gian quy định 4 ngày, tổ đã may được 6416 chiếc khẩu trang nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{8400}}{x} - \dfrac{{6416}}{{x + 102}} = 4\\ \Leftrightarrow \dfrac{{2100}}{x} - \dfrac{{1604}}{{x + 102}} = 1\\ \Leftrightarrow 2100\left( {x + 102} \right) - 1604x = x\left( {x + 102} \right)\\ \Leftrightarrow 2100x + 214200 - 1604x = {x^2} + 102x\\ \Leftrightarrow {x^2} - 394x - 214200 = 0\\ \Leftrightarrow {x^2} - 700x + 306x - 214200 = 0\\ \Leftrightarrow x\left( {x - 700} \right) + 306\left( {x - 700} \right) = 0\\ \Leftrightarrow \left( {x - 700} \right)\left( {x + 306} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 700\,\,\left( {tm} \right)\\x = - 306\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy số khẩu trang mà tổ phải may mỗi ngày theo kế hoạch là \(700\) chiếc.
Câu 6
Phương pháp:
Áp dụng định lí Pytago trong tam giác vuông \(ABC\), tính được \(BC\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\), tính được \(AH\).
Cách giải:
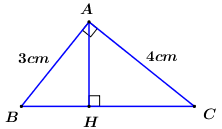
Áp dụng định lí Pytago trong tam giác vuông \(ABC\) ta có:
\(\begin{array}{l}\,\,\,\,\,B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {3^2} + {4^2} = 9 + 16 = 25\\ \Rightarrow BC = \sqrt {25} = 5\,\,\left( {cm} \right)\end{array}\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), đường cao \(AH\) ta có:
\(AB.AC = AH.BC \Rightarrow AH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{3.4}}{5} = 2,4\,\,\left( {cm} \right)\).
Vậy \(BC = 5\,\,cm,\,\,AH = 2,4\,\,cm\).
Câu 7:
Phương pháp:
a) Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Gọi \(N\) là giao điểm của \(AB\) với \(MO\).
\(C\) là giao điểm giữa \(MK\) với đường tròn \(\left( O \right)\)
Ta sẽ chứng minh: \(\left\{ \begin{array}{l}NI//BK\\NA = NB = \dfrac{1}{2}AB\end{array} \right.\)
Suy ra \(I\) là trung điểm của \(AH\)
\( \Rightarrow IA = IH\) (định lí đường trung bình của tam giác)
Cách giải:
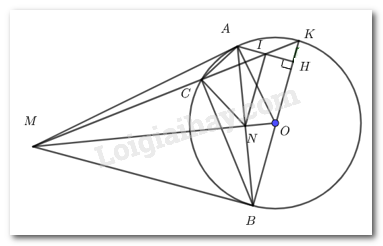
a) Vì \(MA,\,\,MB\) là các tiếp tuyến của \(\left( O \right)\) lần lượt tại \(A,\,\,B\) nên \(\angle MAO = \angle MBO = {90^0}\) (định nghĩa).
Tứ giác \(MAOB\) có \(\angle MAO + \angle MBO = {180^0}\).
Suy ra tứ giác \(MAOB\) nội tiếp (tứ giác có tổng hai góc đối bằng bằng \({180^0}\)).
b) Gọi \(N\) là giao điểm của \(AB\) với \(MO\).
\(C\) là giao điểm giữa \(MK\) với đường tròn \(\left( O \right)\)
Ta có: \(OA = OB \Rightarrow O\) thuộc trung trực của \(AB\).
\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) nên \(M\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB\) \( \Rightarrow OM \bot AB\) tại \(N\).
Tứ giác \(MCNB\) có \(\angle MCB = \angle MNB = {90^0}\). Suy ra tứ giác \(MCNB\) nội tiếp (tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle NMB = \angle NCB\) (hai góc cùng chắn một cung \(BN\))
Ta có: \(\angle NMB = \angle NBO\) (cùng phụ với \(\angle MBN\))
\( \Rightarrow \angle NCB = \angle NBO\).
Lại có: \(\angle NCB + \angle NCI = {90^0},\,\,\,\angle NAI + \angle NBO = {90^0}\)
Suy ra \(\angle NCI = \angle NAI\).
Xét tứ giác \(ACNI\) có: \(\angle NCI = \angle NAI\) (cmt), suy ra tứ giác \(ACNI\) nội tiếp (tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle ANI = \angle ACI\) (hai góc cùng chắn cung \(AI\)).
Trong \(\left( O \right)\) có: \(\angle ACI = \angle ABK\) (hai góc nội tiếp cùng chắn cung \(AK\))
Suy ra \(\angle ANI = \angle ABK\). Mà hai góc này vị trí đồng vị \( \Rightarrow NI//BK\)
Tam giác \(ABK\) có: \(\left\{ \begin{array}{l}NI//BK\\NA = NB = \dfrac{1}{2}AB\end{array} \right.\)
Suy ra \(I\) là trung điểm của \(AH\)
\( \Rightarrow IA = IH\) (định lí đường trung bình của tam giác) (đpcm).
