Đề bài
Câu 1 (3 điểm):
1) Tính giá trị của biểu thức: \(A = \sqrt {4 - 2\sqrt 3 } - \dfrac{1}{2}\sqrt {12} .\)
2) Giải phương trình và hệ phương trình sau:
\(a)\;{x^4} + {x^2} - 20 = 0\) \(b)\;\left\{ \begin{array}{l}3x - y = 11\\2x + y = 9\end{array} \right..\)
3) Cho phương trình \({x^2} - 2x - 5 = 0\) có hai nghiệm \({x_1},\;{x_2}.\) Không giải phương trình, hãy tính giá trị của các biểu thức: \(B = x_1^2 + x_2^2,\;\;C = x_1^5 + x_2^5.\)
Câu 2 (2 điểm): Trong mặt phẳng tọa độ \(Oxy\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;\;y = x + m.\)
1) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng một hệ trục tọa độ khi \(m = 2.\)
2) Định các giá trị của \(m\) để \(\left( d \right)\)cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B.\)
3) Tìm giác trị của \(m\) để độ dài đoạn thẳng \(AB = 6\sqrt 2 .\)
Câu 3 (1,5 điểm): Hai bến sông A và B cách nhau 60km. Một ca nô đi xuôi dòng từ A đến B rồi ngược dòng về A. Thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 20 phút. Tính vận tốc ngược dòng của ca nô, biết vận tốc xuôi dòng lớn hơn vận tốc ngược dòng của ca nô là 6 km/h.
Câu 4 (2,5 điểm): Cho tam giác ABC có ba góc nhọn (AB < AC), các đường cao AF, BD và CE cắt nhau tại H.
1) Chứng minh tứ giác BEDC nội tiếp đường tròn.
2) Chứng minh AE.AB = AD.AC.
3) Chứng minh FH là phân giác của \(\widehat {EFD}.\)
4) Gọi O là trung điểm của đoạn thẳng BC. Chứng minh \(\widehat {DOC} = \widehat {FED}.\)
Câu 5 (1 điểm): Một hình trụ có diện tích xung quanh bằng \(256\pi c{m^2}\) và bán kính đáy bằng \(\dfrac{1}{2}\) đường cao. Tính bán kính đáy và thể tích hình trụ.
Lời giải
Câu 1:
Phương pháp:
1) Sử dụng công thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\;\;khi\;\;A \ge 0\\ - A\;\;khi\;\;A < 0\end{array} \right..\)
2) a) Đặt \({x^2} = t\;\;\left( {t \ge 0} \right),\) đưa phương trình đã cho về phương trình bậc hai ẩn t. Giải phương trình ẩn t sau đó tìm ẩn x.
b) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
3) Áp dụng hệ thức Vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\) để tính giá trị các biểu thức đề bài yêu cầu.
Cách giải:
\(\begin{array}{l}1)\;\;A = \sqrt {4 - 2\sqrt 3 } - \dfrac{1}{2}\sqrt {12} \\\;\;\;\;\;\;\; = \sqrt {{{\left( {\sqrt 3 } \right)}^2} - 2.\sqrt 3 .1 + 1} - \dfrac{1}{2}.\sqrt {{2^2}.3} \\\;\;\;\;\;\;\; = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} - \dfrac{{2\sqrt 3 }}{2}\\\;\;\;\;\;\;\; = \left| {\sqrt 3 - 1} \right| - \sqrt 3 \\\;\;\;\;\;\;\; = \sqrt 3 - 1 - \sqrt 3 = - 1.\;\;\left( {do\;\;\sqrt 3 - 1 > 0} \right).\end{array}\)
2) Giải phương trình và hệ phương trình sau:
\(a)\;{x^4} + {x^2} - 20 = 0\)
Đặt \({x^2} = t\;\;\left( {t \ge 0} \right).\) Khi đó ta có phương trình:
\(\begin{array}{l} \Leftrightarrow {t^2} + t - 20 = 0\\ \Leftrightarrow {t^2} + 5t - 4t - 20 = 0\\ \Leftrightarrow \left( {t - 4} \right)\left( {t + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t - 4 = 0\\t + 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 4\;\;\left( {tm} \right)\\t = - 5\;\;\left( {ktm} \right)\end{array} \right.\\ \Rightarrow {x^2} = 4 \Leftrightarrow x = \pm 2.\end{array}\)
Vậy phương trình có tập nghiệm \(S = \left\{ { - 2;\;2} \right\}.\)
\(b)\;\left\{ \begin{array}{l}3x - y = 11\\2x + y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 20\\y = 9 - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 9 - 2.4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 1\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\;y} \right) = \left( {4;1} \right).\)
3) Cho phương trình \({x^2} - 2x - 5 = 0\) có hai nghiệm \({x_1},\;{x_2}.\) Không giải phương trình, hãy tính giá trị của các biểu thức: \(B = x_1^2 + x_2^2,\;\;C = x_1^5 + x_2^5.\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = - 5\end{array} \right..\)
Khi đó: \(B = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {2^2} - 2.\left( { - 5} \right) = 14.\)
\(\begin{array}{l}C = x_1^5 + x_2^5 = \left( {{x_1} + {x_2}} \right)\left( {x_1^4 - x_1^3{x_2} + x_1^2x_2^2 - {x_1}x_2^3 + x_2^4} \right)\\\;\;\; = \left( {{x_1} + {x_2}} \right)\left[ {x_1^4 + x_2^4 - {x_1}{x_2}\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2} \right]\\\;\;\; = \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {x_1^2 + x_2^2} \right)}^2} - 2x_1^2x_2^2 - {x_1}{x_2}\left( {x_1^2 + x_2^2} \right) + x_1^2x_2^2} \right]\\\;\;\; = \left( {{x_1} + {x_2}} \right)\left[ {{{\left( {x_1^2 + x_2^2} \right)}^2} - {x_1}{x_2}\left( {x_1^2 + x_2^2} \right) - x_1^2x_2^2} \right].\end{array}\)
Áp dụng hệ thức Vi-ét và kết quả của biểu thức B ta được:
\(C = 2\left[ {{{14}^2} - \left( { - 5} \right).14 - {{\left( { - 5} \right)}^2}} \right] = 2.\left( {196 + 70 - 25} \right) = 482.\)
Câu 2:
Phương pháp:
1) Lập bảng giá trị mà các đồ thị hàm số đi qua sau đó vẽ hai đồ thị trên cùng một hệ trục tọa độ.
2) Để \(\left( d \right)\)cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\) thì phương trình hoành độ giao điểm của hai đồ thị có hai nghiệm phân biệt \( \Leftrightarrow \Delta > 0.\)
3) +) Áp dụng hệ thức Vi-ét \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..\)
+) Sử dụng công thức tính đoạn thẳng: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} .\)
Cách giải:
Trong mặt phẳng tọa độ \(Oxy\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;\;y = x + m.\)
1) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng một hệ trục tọa độ khi \(m = 2.\)
+) Với \(m = 2\) ta có: \(\left( d \right):\;\;y = x + 2.\)
Ta có bảng giá trị:
|
\(x\) |
\(0\) |
\( - 2\) |
|
\(y = x + 2\) |
\(2\) |
\(0\) |
Đường thẳng \(\left( d \right)\) đi qua hai điểm \(\left( {0;\;2} \right)\) và \(\left( { - 2;\;0} \right).\)
+) Vẽ đồ thị hàm số \(\left( P \right):\)
|
\(x\) |
\( - 4\) |
\( - 2\) |
\(0\) |
\(2\) |
\(4\) |
|
\(y = \dfrac{1}{2}{x^2}\) |
\(8\) |
\(2\) |
\(0\) |
\(2\) |
\(8\) |
Đồ thị \(\left( P \right)\) là đường cong đi qua các điểm \(\left( { - 4;\;8} \right),\;\;\left( { - 2;\;2} \right),\;\left( {0;\;0} \right),\;\left( {2;\;2} \right),\;\;\left( {4;\;8} \right).\)
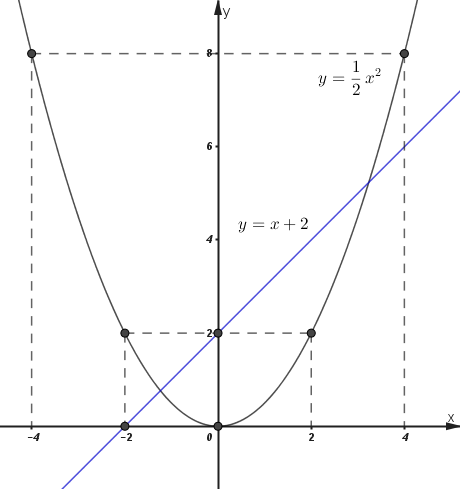
2) Định các giá trị của \(m\) để \(\left( d \right)\)cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B.\)
Phương trình hoành độ giao điểm của hai đồ thị là: \(x + m = \dfrac{1}{2}{x^2} \Leftrightarrow {x^2} - 2x - 2m = 0.\;\;\left( * \right)\)
Để \(\left( d \right)\)cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B\) thì phương trình \(\left( * \right)\) có nghiệm hai phân biệt \( \Leftrightarrow \Delta ' > 0\)
\( \Leftrightarrow 1 + 2m > 0 \Leftrightarrow m > - \dfrac{1}{2}.\)
Vậy \(m > - \dfrac{1}{2}.\)
3) Tìm giác trị của \(m\) để độ dài đoạn thẳng \(AB = 6\sqrt 2 .\)
Với \(m > - \dfrac{1}{2}\) thì \(\left( d \right)\)cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};\;{y_1}} \right),\;\;B\left( {{x_2};\;{y_2}} \right).\)
Khi đó \({x_1},\;{x_2}\) là hai nghiệm của phương trình \(\left( * \right).\) Áp dụng hệ thức Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = - 2m\end{array} \right..\)
Ta có: \(A,\;\;B \in \left( d \right) \Rightarrow A\left( {{x_1};\;{x_1} + m} \right),\;\;B\left( {{x_2};\;x + m} \right).\)
Theo đề bài ta có: \(AB = 6\sqrt 2 \)
\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} = 6\sqrt 2 \\ \Leftrightarrow \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_2} + m - {x_1} - m} \right)}^2}} = 6\sqrt 2 \\ \Leftrightarrow \sqrt {2{{\left( {{x_2} - {x_1}} \right)}^2}} = 6\sqrt 2 \\ \Leftrightarrow {\left( {{x_2} - {x_1}} \right)^2} = 36\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 36\\ \Leftrightarrow {2^2} - 4.\left( { - 2m} \right) = 36\\ \Leftrightarrow 8m = 32\\ \Leftrightarrow m = 4\;\;\left( {tm} \right).\end{array}\)
Vậy \(m = 4.\)
Câu 3:
Phương pháp:
Giải bài toàn bằng cách lập phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diễn các đại lượng chữa biết theo ẩn và đại lượng đã biết.
+) Dựa vào giả thiết của bài toán để lập phương trình.
+) Giải phương trình tìm ẩn và đối chiếu với điều kiện của ẩn rồi kết luận.
Cách giải:
Hai bến sông A và B cách nhau 60km. Một ca nô đi xuôi dòng từ A đến B rồi ngược dòng về A. Thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 20 phút. Tính vận tốc ngược dòng của ca nô, biết vận tốc xuôi dòng lớn hơn vận tốc ngược dòng của ca nô là 6 km/h.
Gọi vận tốc ngược dòng của ca nô là \(x\;\left( {km/h} \right)\;\;\left( {x > 0} \right).\)
Khi đó vận tốc ca nô khi xuôi dòng là: \(x + 6\;\;\left( {km/h} \right).\)
Thời gian ca nô đi hết khúc sông khi xuôi dòng là: \(\dfrac{{60}}{{x + 6}}\;\left( h \right).\)
Thời gian ca nô đi hết khúc sông khi ngược dòng là: \(\dfrac{{60}}{x}\;\left( h \right).\)
Theo đề bài ta có phương trình: \(\dfrac{{60}}{x} - \dfrac{{60}}{{x + 6}} = \dfrac{{20}}{{60}} = \dfrac{1}{3}\)
\(\begin{array}{l} \Leftrightarrow 3.60\left( {x + 6} \right) - 3.60x = x\left( {x + 6} \right)\\ \Leftrightarrow 180x + 1080 - 180x = {x^2} + 6x\\ \Leftrightarrow {x^2} + 6x - 1080 = 0\\ \Leftrightarrow \left( {x - 30} \right)\left( {x + 36} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 30 = 0\\x + 36 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 30\;\;\left( {tm} \right)\\x = - 36\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)
Vậy vận tốc của ca nô khi ngược dòng là \(30\;km/h.\)
Câu 4:
Phương pháp:
1) Chứng minh tứ giác BEDC có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện.
2) Chứng minh tam giác ABC đồng dạng với tam giác ADE.
3) Chứng minh các tứ giác BEHF và CDHF là các tứ giác nội tiếp.
4) Chứng minh \(\widehat {DOC} = \widehat {DEF} = 2\widehat {{B_1}}\).
Cách giải:
Cho tam giác ABC có ba góc nhọn (AB < AC), các đường cao AF, BD và CE cắt nhau tại H.
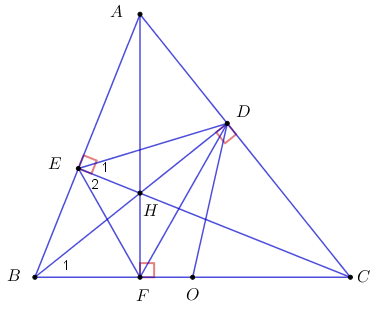
1) Chứng minh tứ giác BEDC nội tiếp đường tròn.
Xét tứ giác \(BEDC\) ta có: \(\widehat {BEC} = \widehat {BDC} = {90^0}\;\left( {gt} \right)\)
Mà hai góc này là hai góc kề 1 cạnh và cùng nhìn đoạn \(BC.\)
\( \Rightarrow BEDC\) là tứ giác nội tiếp (dấu hiệu nhận biết).
2) Chứng minh AE.AB = AD.AC.
Vì \(BEDC\) là tứ giác nội tiếp (cmt) nên \(\widehat {ADE} = \widehat {ABC}\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện).
Xét \(\Delta ADE\) và \(\Delta ABC\) ta có:
\(\begin{array}{l}\widehat A\;chung\\\widehat {AED} = \widehat {ABC}\;\;\left( {cmt} \right)\\ \Rightarrow \Delta ADE \sim \Delta ABC\;\left( {g - g} \right).\\ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} \Leftrightarrow AD.AC = AE.AB\;\;\left( {dpcm} \right).\end{array}\)
3) Chứng minh FH là phân giác của \(\widehat {EFD}.\)
Ta có: \(BEHF\) là tứ giác nội tiếp \(\left( {do\;\;\widehat {BEH} + \widehat {HFB} = {{90}^0} + {{90}^0} = {{180}^0}} \right).\)
\( \Rightarrow \widehat {EBH} = \widehat {EFH}\) (hai góc nội tiếp cùng chắn cung \(EH\)) (1)
Có \(DCFH\) là tứ giác nội tiếp \(\left( {do\;\;\widehat {HFC} + \widehat {HDC} = {{90}^0} + {{90}^0} = {{180}^0}} \right).\)
\( \Rightarrow \widehat {DCH} = \widehat {DFH}\) (hai góc nội tiếp cùng chắn cung \(DH\)) (2)
Mà \(BEDC\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \widehat {DCH} = \widehat {EBH}\) (hai góc nội tiếp cùng chắn cung \(DE\)) (3)
Từ (1), (2) và (3) ta có: \(\widehat {EFH} = \widehat {HFD}.\)
Hay \(FH\) là phân giác của \(\widehat {EFD}.\) (đpcm)
4) Gọi O là trung điểm của đoạn thẳng BC. Chứng minh \(\widehat {DOC} = \widehat {FED}.\)
Xét tam giác \(BDC\) vuông tại \(D\) có đường trung tuyến \(DO \Rightarrow DO = OB = OC\) (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông).
\( \Rightarrow \Delta BOD\) cân tại \(O \Rightarrow \widehat {BDO} = \widehat {DBO}\) (tính chất tam giác cân)
\( \Rightarrow \widehat {DOC} = \widehat {DBO} + \widehat {BDO} = 2\widehat {DBO} = 2\widehat {{B_1}}.\)
Vì \(EBCD\) là tứ giác nội tiếp \( \Rightarrow \widehat {{B_1}} = \widehat {{E_1}}\) (hai góc nội tiếp cùng chắn cung \(CD\))
Vì \(BEHF\) là tứ giác nội tiếp \( \Rightarrow \widehat {{B_1}} = \widehat {{E_2}}\) (hai góc nội tiếp cùng chắn cung \(HF\))
\( \Rightarrow \widehat {DOC} = 2\widehat {{B_1}} = \widehat {{E_1}} + \widehat {{E_2}} = \widehat {FED}.\;\;\;\left( {dpcm} \right)\)
Câu 5:
Phương pháp:
Sử dụng các công thức \({S_{xq}} = 2\pi Rh\) và \({V_{tru}} = \pi {R^2}h\) trong đó R, h lần lượt là bán kính đáy và chiều cao của hình trụ.
Cách giải :
Một hình trụ có diện tích xung quanh bằng \(256\pi c{m^2}\) và bán kính đáy bằng \(\dfrac{1}{2}\) đường cao. Tính bán kính đáy và thể tích hình trụ.
Gọi R, h lần lượt là bán kính đáy và chiều cao của hình trụ.
Vì bán kính đáy bằng \(\dfrac{1}{2}\) đường cao nên \(R = \dfrac{1}{2}h \Rightarrow h = 2R\)
Khi đó ta có \({S_{xq}} = 2\pi Rh = 2\pi .R.2R = 256\pi \Leftrightarrow {R^2} = 64 \Leftrightarrow R = 8\,\,\left( {cm} \right)\)
\( \Rightarrow h = 2.8 = 16\,\,\left( {cm} \right)\)
Vậy thể tích của khối trụ là \(V = \pi {R^2}h = \pi {.8^2}.16 = 1024\pi \,\,\left( {c{m^3}} \right)\).
