1. Lý thuyết
+ Định nghĩa:
Tập xác định của hàm số \(y = f(x)\) là tập hợp tất cả các số thực x sao cho biểu thức \(f(x)\) có nghĩa.
Tập giá trị của hàm số \(y = f(x)\) là tập hợp tất cả các giá trị \(f(x)\) tương ứng với x thuộc tập xác định.
+ Kí hiệu:
Tập xác định thường kí hiệu là D. Ta nói: \(x \in D\) là điều kiện xác định của hàm số.
Tập giá trị thường kí hiệu là T.
+ Điều kiện xác định của một số biểu thức
\(\sqrt {f(x)} \) xác định khi \(f(x) \ge 0\)
\(\frac{1}{{f(x)}}\) xác định khi \(f(x) \ne 0\)
\(\frac{1}{{\sqrt {f(x)} }}\) xác định khi \(f(x) > 0\)
2. Ví dụ minh họa
Dạng bảng
Tập xác định là tập hợp các giá trị x có trong bảng.
Tập giá trị là tập hợp các giá trị y có trong bảng.
Ví dụ: Dự báo thời tiết ngày 2/11/2022 tại Hà Nội
|
Giờ |
1 |
4 |
7 |
10 |
13 |
16 |
19 |
22 |
|
Nhiệt độ \({(^o}C)\) |
19 |
17 |
22 |
26 |
29 |
27 |
25 |
23 |
Tập xác định \(D = \{ 1;4;7;10;13;16;19;22\} \)
Tập giá trị \(T = \{ 19;17;22;26;29;27;25;23\} \).
Dạng biểu đồ
Ví dụ: Dự báo thời tiết ngày 20/11/2021 tại Hà Nội
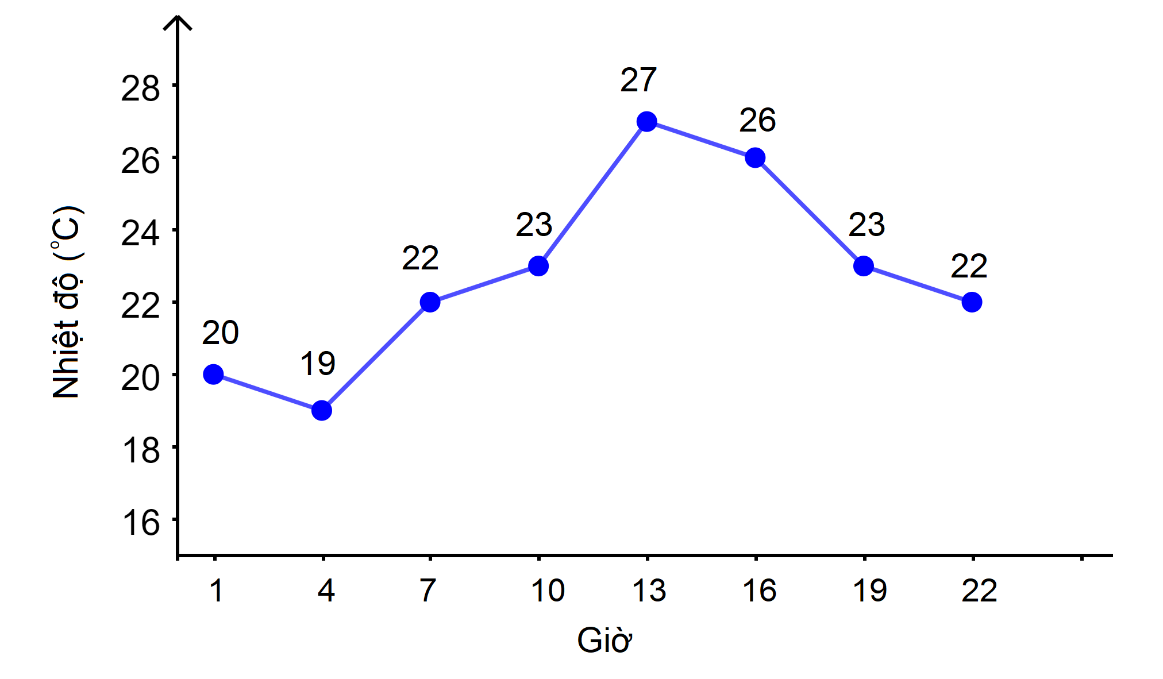
Tập xác định \(D = \{ 1;4;7;10;13;16;19;22\} \)
Tập giá trị \(T = \{ 20;19;22;23;27;26\} \).
Dạng công thức
Ví dụ:
\(y = {x^2} + 3\), biểu thức có nghĩa với mọi \(x \in \mathbb{R}\) nên tập xác định là \(D = \mathbb{R}\)
\(y = \sqrt {x - 1} \), biểu thức có nghĩa nếu \(x - 1 \ge 0\) hay \(x \ge 1\). Vậy tập xác định \(D = [1; + \infty )\)
\(y = \left\{ \begin{array}{l} - 3x + 5\quad \quad x \le 1\\2{x^2}\quad \quad \quad \;\;x > 2\end{array} \right.\), ta xác đinh được y với \(x \le 1\) hoặc \(x > 2\), do đó tập xác định là \(D = ( - \infty ;1] \cup (2; + \infty )\)
