Đề bài
I. TRẮC NGHIỆM (2 điểm)
Câu 1 : Phân thức: \(\dfrac{{{x^2} - 2017}}{{1 + {x^{2018}}}}\) xác định với:
A. \(x \ne 1\) B. \(x \ne - 1\)
C.\(x \ne 0\) D.\(\forall x \in R\)
Câu 2 : Biểu thức P trong đẳng thức: \(\dfrac{{4{x^2} - 16}}{{2x + {x^2}}} = \dfrac{P}{x}\) là:
A.\(\dfrac{{4x - 8}}{x}\) B. \(4x - 8\)
C.\(2x - 4\) D.\(2x - 2\)
Câu 3 : Hình vuông có đường chéo bằng \(2\,dm\) thì cạnh bằng:
A. \(\dfrac{3}{2}\,dm\) B. \(1\,dm\)
C.\(\sqrt 2 \,dm\) D.\(2\,dm\)
Câu 4 : Hình thoi có hai đường chéo bằng \(6\,cm\)và \(8\,cm\)thì cạnh bằng:
A. \(5\,cm\) B. \(10\,cm\)
C.\(12,5\,cm\) D.\(7\,cm\)
II. TỰ LUẬN (8 điểm)
Bài 1 Phân tích đa thức thành nhân tử:
a)\({x^2} + 2x\)
b)\({x^3} - 5{x^2} + 5x - 1\)
Bài 2 Thực hiện phép tính:
a)\(\left( {{x^3} + {x^2} - 3x + 9} \right):\left( {x + 3} \right)\)
b)\(\dfrac{{4x - 8}}{{x + 5}}:\dfrac{{25 - {x^2}}}{{2x - {x^2}}}\)
Bài 3 (2,0 điểm)Cho biểu thức: \(A = \dfrac{1}{{x + 1}} + \dfrac{{x - 1}}{x} + \dfrac{{x + 2}}{{{x^2} + x}}\)
a)Tìm giá trị của \(x\)để giá trị của biểu thức A xác định.
b)Rút gọn A.
Bài 4 Cho hình vuông \(ABC{\rm{D}}\). Trên các cạnh \(AB,\,BC,\,C{\rm{D}},\,DA\) lần lượt lấy các điểm \(M,\,N,\,E,\,F\) sao cho \(AM = CN = CE = AF\).
a)Chứng minh tứ giác \(ANCF\) là hình bình hành.
b)Chứng minh tứ giác \(MNEF\) là hình chữ nhật.
c)Gọi \(H\) là hình chiếu của \(A\) trên \(BF\). Tính \(\angle CHM\).
Bài 5 : Cho \(x + y = 2\) chứng minh: \({x^{2017}} + {y^{2017}} \le {x^{2018}} + {y^{2018}}\)
LG trắc nghiệm
Lời giải chi tiết:
I. TRẮC NGHIỆM
|
Câu 1 |
Câu 2 |
Câu 3 |
Câu 4 |
|
D |
B |
C |
A |
LG bài 1
Lời giải chi tiết:
\(a)\,\,{x^2} + 2x\,{\rm{ = }}\,x\left( {x + 2} \right)\)
\(\begin{array}{l}b)\;{x^3} - 5{x^2} + 5x - 1 \\= \left( {{x^3} - 1} \right) - \left( {5{x^2} - 5x} \right)\\ = \left( {x - 1} \right)\left( {{x^2} + x + 1} \right) - 5x\left( {x - 1} \right)\\ = \left( {x - 1} \right)\left( {{x^2} + x + 1 - 5x} \right) \\= \left( {x - 1} \right)\left( {{x^2} - 4x + 1} \right).\end{array}\)
LG bài 2
Lời giải chi tiết:
\(b)\,\,\dfrac{{4x - 8}}{{x + 5}}:\dfrac{{25 - {x^2}}}{{2x - {x^2}}}\)
\(= \dfrac{{4\left( {x - 2} \right)}}{{x + 5}}.\dfrac{{x\left( {2 - x} \right)}}{{\left( {5 + x} \right)\left( {5 - x} \right)}}\)
\(= \dfrac{{ - 4x{{\left( {x - 2} \right)}^2}}}{{{{\left( {x + 5} \right)}^2}\left( {5 - x} \right)}} \)
\(= \dfrac{{4x{{\left( {x - 2} \right)}^2}}}{{{{\left( {x + 5} \right)}^2}\left( {x - 5} \right)}}.\)
LG bài 3
Lời giải chi tiết:
Bài 3
a) Phân thức \(A\)được xác định\( \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne - 1\end{array} \right.\)
\(\begin{array}{l}b)\,\,A = \dfrac{1}{{x + 1}} + \dfrac{{x - 1}}{x} + \dfrac{{x + 2}}{{{x^2} + x}} \\= \dfrac{{x + \left( {x - 1} \right)\left( {x + 1} \right) + x + 2}}{{x\left( {x + 1} \right)}}\\ = \dfrac{{2x + {x^2} - 1 + 2}}{{x\left( {x + 1} \right)}} \\= \dfrac{{{x^2} + 2x + 1}}{{x\left( {x + 1} \right)}}\\ = \dfrac{{{{\left( {x + 1} \right)}^2}}}{{x\left( {x + 1} \right)}} = \dfrac{{x + 1}}{x}\end{array}\)
LG bài 4
Lời giải chi tiết:
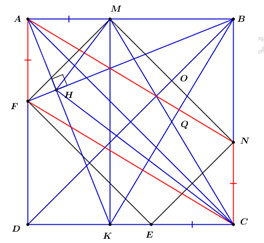
a)Vì \(ABC{\rm{D}}\) là hình vuông (gt)
\( \Rightarrow A{\rm{D}}//BC\)(tính chất hình vuông)
\( \Rightarrow AF//NC\) mà \(AF = NC\left( {gt} \right) \Rightarrow ANCF\) là hình bình hành (dhnb)
b)Vì \(ABC{\rm{D}}\) là hình vuông (gt)
\( \Rightarrow A{\rm{D}}\,{\rm{ = }}\,BC = DC = AB\) (tính chất hình vuông)
Mà \(\left\{ \begin{array}{l}AF = NC\\NC = EC\end{array} \right.\left( {gt} \right) \Rightarrow \left\{ \begin{array}{l}\dfrac{{AF}}{{A{\rm{D}}}} = \dfrac{{AM}}{{AB}}\\\dfrac{{NC}}{{BC}} = \dfrac{{EC}}{{DC}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}FM//B{\rm{D}}\\EN//B{\rm{D}}\end{array} \right.\) (định lý Ta-let )\( \Rightarrow FM//EN\)(1)
Xét \({\Delta }AMF\) và \({\Delta }CNE\) có:
\(\left\{ \begin{array}{l}AM = NC\\AF = CE\end{array} \right.\left( {gt} \right)\)
\(\Rightarrow {\Delta }AMF = {\Delta }CNE\) (2 cạnh góc vuông)
\( \Rightarrow MF = EN\) (2 cạnh tương ứng) (2)
Từ (1) và (2) \( \Rightarrow FMNE\) là hình bình hành (dhnb)
Vì \(ABC{\rm{D}}\) là hình vuông (gt) \( \Rightarrow B{\rm{D}}\) là phân giác của \(\angle ABC\) (tính chất hình vuông)
\( \Rightarrow \angle AB{\rm{D}} = \angle DBC\) (tính chất tia phân giác) hay \(\angle MB{\rm{D}} = \angle NB{\rm{D}}\)
Ta có: \(\left\{ \begin{array}{l}AM = NC\\AB = BC\\MB = AB - AM\\BN = BC - NC\end{array} \right.\left( {gt} \right) \Rightarrow MB = BN\)
Gọi \(MN \cap B{\rm{D}} = \left\{ O \right\}\)
Xét \(\Delta MBO\) và \(\Delta NBO\) có:
\(\left\{ \begin{array}{l}MB = BN\,\left( {cmt} \right)\\BO\,chung\,\,\left( {gt} \right)\\\angle MBO = \angle OBN\left( {cmt} \right)\end{array} \right. \\\Rightarrow \Delta MBO = \Delta NBO\left( {c - g - c} \right) \\\Rightarrow \angle MOB = \angle BON\) (2 góc tương ứng)
Mà \(\angle MOB + \angle BON = {180^0} \)
\(\Rightarrow \angle MOB = \angle BON = {90^0} \Rightarrow BO \bot MN\)
Mà \(FM//B{\rm{D}} \Rightarrow FM \bot MN \Rightarrow \angle FMN = {90^0}\)
Do đó hình bình hành \(FMNE\) là hình chữ nhật (dhnb)
c) Gọi \(AH\) cắt \(C{\rm{D}}\) tại \(K\).
Xét \({\Delta }ABF\) có: \(\angle ABF + \angle AFB = {90^0}\) (2 góc nhọn phụ nhau)
Xét \({\Delta }AHF\) có: \(\angle AFH + \angle FAH = {90^0} \Rightarrow \angle AFB + \angle FAH = {90^0}\) (2 góc nhọn phụ nhau)
\( \Rightarrow \angle FAH = \angle ABF\)
Xét \({\Delta }ABF\) và \({\Delta }DAK\) có:
\(\left\{ \begin{array}{l}AB = A{\rm{D}}\left( {gt} \right)\\\angle ABF = \angle FAH\left( {cmt} \right)\end{array} \right. \Rightarrow {\Delta }ABF = {\Delta }DAK\) (cạnh góc vuông – góc nhọn)
\( \Rightarrow AF = DK\) (2 cạnh tương ứng)
Mà \(AF = AM\left( {gt} \right) \Rightarrow AM = DK\)
Lại có: \(\left\{ \begin{array}{l}AB = DC\left( {gt} \right)\\AM = DK\left( {cmt} \right)\\BM = AB - AM\left( {gt} \right)\\CK = DC - DK\left( {gt} \right)\end{array} \right. \Rightarrow BM = CK\)(3)
Mà \(AB//DC\left( {gt} \right) \Rightarrow BM//KC\) (4)
Từ (3) và (4) suy ra \(MBCK\) là hình bình hành (dhnb)
Lại có, \(\angle MBC = {90^0}\left( {gt} \right) \Rightarrow \) hình bình hành \(MBCK\) là hình chữ nhật (dhnb)
\( \Rightarrow MC = BK\) (tính chất)
Gọi \(Q\) là giao điểm của \(MC\) và \(BK\)\( \Rightarrow Q\) là trung điểm của mỗi đường.
Xét \({\Delta }BHK\) có: \(QH = \dfrac{{BK}}{2} = \dfrac{{MC}}{2}\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
\( \Rightarrow \Delta MHC\) vuông tại \(H\) (trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)\( \Rightarrow \angle CHM = {90^0}\)
LG bài 5
Lời giải chi tiết:
Vì \(x + y = 2\) nên ta có:
\(\begin{array}{l}{x^{2017}} + {y^{2017}} \le {x^{2018}} + {y^{2018}}\\ \Leftrightarrow \left( {x + y} \right)\left( {{x^{2017}} + {y^{2017}}} \right) \le 2\left( {{x^{2018}} + {y^{2018}}} \right)\\ \Leftrightarrow {x^{2018}} + x{y^{2017}} + {x^{2017}}y + {y^{2018}} \le 2{x^{2018}} + 2{y^{2018}}\\ \Leftrightarrow {x^{2018}} - 2{x^{2018}} + x{y^{2017}} + {x^{2017}}y + {y^{2018}} - 2{y^{2018}} \le 0\\ \Leftrightarrow {x^{2018}} + {y^{2018}} - {x^{2017}}y - x{y^{2017}} \ge 0\\ \Leftrightarrow \left( {x - y} \right)\left( {{x^{2017}} - {y^{2017}}} \right) \ge 0\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - y \ge 0\\{x^{2017}} - {y^{2017}} \ge 0\end{array} \right.\\\left\{ \begin{array}{l}x - y \le 0\\{x^{2017}} - {y^{2017}} \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge y\\{x^{2017}} \ge {y^{2017}}\end{array} \right.\\\left\{ \begin{array}{l}x \le y\\{x^{2017}} \le {y^{2017}}\end{array} \right.\end{array} \right.\end{array}\)
\( \Rightarrow \)Bất đẳng thức luôn đúng với mọi \(x,\;y\) thỏa mãn \(x + y = 2.\)
Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 8 tại Tuyensinh247.com
soanvan.me
