Đề bài
Tam giác \(ABC\) có các đường cao \(BD, CE\) cắt nhau tại \(H\). Đường vuông góc với \(AB\) tại \(B\) và đường vuông góc với \(AC\) tại \(C\) cắt nhau ở \(K\). Tam giác \(ABC\) phải có điều kiện gì thì tứ giác \(BHCK\) là:
a) Hình thoi?
b) Hình chữ nhật?
Phương pháp giải - Xem chi tiết
Áp dụng: Dấu hiệu nhận biết hình bình hành, hình thoi.
Lời giải chi tiết
(h.112)
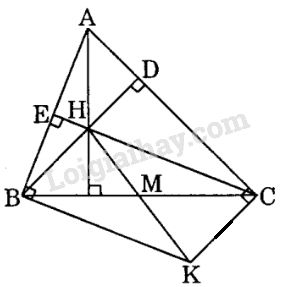
Theo đề bài \(BD \bot AC,KC \bot AC\left( {h.112} \right)\) suy ra \(BD//KC\) hay \(BH//AC;CE \bot AB,KB \bot AB\) suy ra \(CE//KB\) hay \(CH//KB\)
Tứ giác \(BHCK\) có \(BH//KC,CH//KB\) nên là hình bình hành.
Gọi \(M\) là giao điểm của \(BC\) và \(HK.\)
a) Hình bình hành \(BHCK\) là hình thoi khi và chỉ khi \(HM \bot BC.\) Vì \(AH \bot BC\) nên \(HM \bot BC \Leftrightarrow A,M,H\) thẳng hàng \( \Leftrightarrow AM \bot BC \Leftrightarrow \Delta ABC\) cân tại \(A.\)
b) Hình bình hành \(BHCK\) là hình chữ nhật khi và chỉ khi \(\widehat {BKC} = {90^0}.\)
\(\widehat {BKC} = {90^0} \Leftrightarrow \widehat {BAC} = {90^0}\) (tứ giác \(ABKC\) đã có \(\widehat {ABK} = \widehat {ACK} = {90^0}\))
\( \Leftrightarrow \Delta ABC\) vuông tại \(A.\)
soanvan.me
