Đề bài
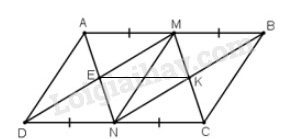
Cho hình bình hành \(ABCD\). Các điểm \(M, N\) theo thứ tự là trung điểm của \(AB, CD\). Gọi \(E\) là giao điểm của \(AN\) và \(DM\), \(K\) là giao điểm của \(BN\) và \(CM\). Hình bình hành \(ABCD\) phải có điều kiện gì để tứ giác \(MENK\) là:
a) Hình thoi?
b) Hình chữ nhật?
c) Hình vuông?
Phương pháp giải - Xem chi tiết
Áp dụng dấu hiệu nhận biết hình bình hành, hình thoi, hình chữ nhật, hình vuông.
Lời giải chi tiết
(h.113)
M, N là trung điểm các cạnh đối AB, CD của hình bình hành ABCD (h.113) nên \(AM = MB = DN = NC\)
Tứ giác MBND có \(MB//DN\) và \(MB = DN\) nên là hình bình hành, suy ra \(MD//BN\) hay \(ME//KN\)
Chứng minh tương tự, ta cũng có: \(EN//MK\)
Tứ giác \(MENK\) có \(ME//KN,EN//MK\) nên là hình bình hành. Ta lại có \(MN//AD\) (do \(AMND\) là hình bình hành), \(EK//CD\) (đường trung bình của tam giác \(MDC\))
a) Hình bình hành \(MENK\) là hình thoi khi và chỉ khi \(MN \bot EK \Leftrightarrow CD \bot AD \Leftrightarrow \) hình bình hành \(ABCD\) là hình chữ nhật
b) Hình bình hành \(MENK\) là hình chữ nhật khi và chỉ khi \(MN = EK \Leftrightarrow AD = DN = \dfrac{1}{2}DC\) (vì \(EK\) là đường trung bình của tam giác \(MDC\))
c) Hình bình hành \(MENK\) là hình vuông khi và chỉ khi \(ABCD\) là hình chữ nhật và \(AD = \dfrac{1}{2}DC\)
soanvan.me