Đề bài
Cho tam giác \(ABC\) có \(AB < AC\), \(D\) là một điểm nằm giữa \(A\) và \(C\). Chứng minh rằng : \(\widehat {ABD} = \widehat {ACB} \Leftrightarrow A{B^2} = AC.AD\)
Phương pháp giải - Xem chi tiết
Áp dụng tính chất của hai tam giác đồng dạng.
Lời giải chi tiết
(h.117)
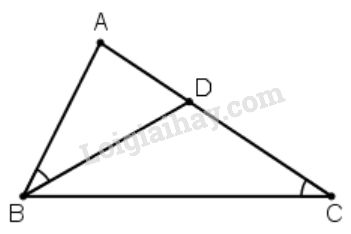
\(\widehat {ABD} = \widehat {ACB}\) (h.117), lại có \(\widehat A\) chung nên \(\Delta ABD \backsim \Delta ACB\left( {g - g} \right),\) suy ra \(\dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AC.AD\) (1)
\(A{B^2} = AC.AD \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}}\) (2), góc \(A\) chung nên \(\Delta ABD \backsim \Delta ACB\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {ABD} = \widehat {ACB}\) (2)
Từ (1) và (2) ta có: \(\widehat {ABD} = \widehat {ACB} \Leftrightarrow A{B^2} = AC.AD\)
soanvan.me
