Đề bài
Cho tam giác \(ABC\) và đường trung tuyến \(BM\). Trên đoạn thẳng \(BM\) lấy điểm \(D\) sao cho \(\dfrac{{B{\rm{D}}}}{{DM}} = \dfrac{1}{2}\) . Tia \(AD\) cắt \(BC\) ở \(K\). Tìm tỉ số diện tích của tam giác \(ABK\) và tam giác \(ABC.\)
Phương pháp giải - Xem chi tiết
Áp dụng:
- Định lí: trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3.
- Công thức tính diện tích tam giác.
Lời giải chi tiết
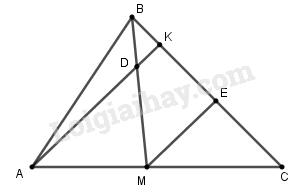
(h.115)
Kẻ \(ME//AK\left( {E \in BC} \right)\) (h.115)
Theo định lý Ta-lét, trong tam giác \(BME\), ta có: \(\dfrac{{BK}}{{KE}} = \dfrac{{BD}}{{DM}} = \dfrac{1}{2}\)
Suy ra \(KE = 2BK.\)
\(M\) là trung điểm của \(AC\) và \(ME//AK\) nên \(E\) là trung điểm của \(KC\).
Ta có: \(EC = KE = 2BK\)
Do đó \(BC = BK + KE + EC = 5BK,\) suy ra \(\dfrac{{BK}}{{BC}} = \dfrac{1}{5}\)
Vậy \(\dfrac{{{S_{ABK}}}}{{{S_{ABC}}}} = \dfrac{{BK}}{{BC}} = \dfrac{1}{5}\) (Hai tam giác \(ABK\) và \(ABC\) có chung đường cao hạ từ \(A\))
soanvan.me