Đề bài
Chu vi hình chữ nhật \(ABCD\) là \(20cm\). Hãy tìm giá trị nhỏ nhất của độ dài đường chéo \(AC\)
Phương pháp giải - Xem chi tiết
+ Gọi độ dài cạnh \(AB\) là \(x\left( {cm} \right),\,\left( {x > 0} \right)\). Tính \(AC\) theo \(x\) (dựa vào định lý Pytago)
+ Biến đổi về dạng \({\left( {x - a} \right)^2} + m \ge m\) để tìm giá trị nhỏ nhất của \(AC.\)
Lời giải chi tiết
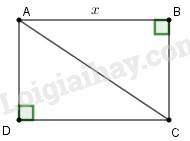
Gọi độ dài cạnh \(AB\) là \(x\left( {cm} \right),\,\left( {x > 0} \right)\) thì độ dài cạnh \(BC\) là
\(\dfrac{20}{2} - AB = 10 - x\left( {cm} \right)\)\(\,\left( {x < 10} \right)\)
Xét tam giác vuông \(ABC\), theo định lý Pytago ta có \(A{C^2} = A{B^2} + B{C^2}\)
\( \Leftrightarrow A{C^2} = {x^2} + {\left( {10 - x} \right)^2}\)\( = {x^2} + 100 - 20x + {x^2} \)\(= 2{x^2} - 20x + 100\) \( = 2\left( {{x^2} - 10x + 25} \right) + 50 \)\(= 2{\left( {x - 5} \right)^2} + 50\)
Vì \(2{\left( {x + 5} \right)^2} \ge 0\) với mọi \(x\) nên \(A{C^2} \ge 50.\)
\(A{C^2} = 50 \Leftrightarrow x = 5\)
Dấu “=” xảy ra \( \Leftrightarrow x - 5 = 0 \Leftrightarrow x = 5\left( {TM} \right)\)
Vậy giá trị nhỏ nhất của đường chéo \(AC\) là \(\sqrt {50} = 5\sqrt 2 \left( {cm} \right)\) khi và chỉ khi \(ABCD\) là hình vuông cạnh \(5cm.\)
soanvan.me
