Đề bài
Cho tam giác \(ABC\) vuông ở \(C\) có đường trung tuyến \(BN\) vuông góc với đường trung tuyến \(CM\), cạnh \(BC = a\). Tính độ dài đường trung tuyến \(BN\).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất trọng tâm và hệ thức lượng trong tam giác vuông: “Bình phương cạnh góc vuông bằng tích hình chiếu của nó lên cạnh huyền với cạnh huyền”
Lời giải chi tiết
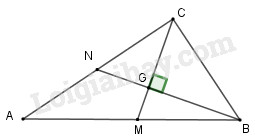
Gọi \(G\) là trọng tâm tam giác \(ABC.\)
Nên \(BG = \dfrac{2}{3}BN\) (tính chất trọng tâm)
Xét tam giác \(BNC\) vuông tại \(C\) có \(BG\) là đường cao nên theo hệ thức lượng trong tam giác vuông thì \(B{C^2} = BG.BN\)
Suy ra \( BN.\dfrac{2.BN}{3}=B{C^2} \)\(\Leftrightarrow \dfrac{2.B{N^2}}{3} = B{C^2}\)\( \Leftrightarrow B{N^2} = \dfrac{3}{2}{a^2}\)
Vậy \( BN = \dfrac{{\sqrt 6 }}{2}a\) .
soanvan.me
