Đề bài
Khi quay tam giác ABC vuông tại A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng \(BC = 4dm,\widehat {ACB} = {30^0}.\) Tính diện tích xung quanh và thể tích hình nón.
Phương pháp giải - Xem chi tiết
+ Xác định độ dài các cạnh của tam giác \(ABC\) dựa vào tỉ số lượng giác của góc nhọn.
+ Hình nón có chiều cao \(h\), bán kính đáy \(R\) và đường sinh \(l\) thì có diện tích xung quanh \({S_{xq}} = \pi Rl\) và thể tích \(V = \dfrac{1}{3}\pi {R^2}h.\)
Lời giải chi tiết
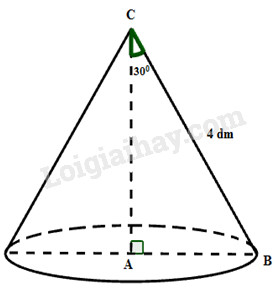
Tam giác \(ABC\) vuông tại \(A\) có \(BC = 4dm;\,\widehat {ACB} = 30^\circ \)
Ta có \(AB=BC.\sin \widehat {ACB}=BC \sin 30^\circ =4. \sin 30^\circ \)\(= \dfrac{1}{2}.4 = 2dm\)
Và \( AC = BC.\cos \widehat {ACB} = 4.\cos 30^\circ \)\( = \dfrac{{4\sqrt 3 }}{2}dm\)
Khi quay tam giác \(ABC\) quanh cạnh \(AC\) ta được một hình nón có chiều cao \(h = AC = \dfrac{{4\sqrt 3 }}{3}dm\), bán kính đáy \(R = AB = 2dm\) và đường sinh \(BC = 4dm\).
Diện tích xung quanh hình nón là \({S_{xq}} = \pi Rl = \pi .2.4 = 8\pi \left( {d{m^2}} \right)\)
Thể tích hình nón là \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.2^2}.\dfrac{{4\sqrt 3 }}{2} = \dfrac{{8\pi \sqrt 3 }}{3}\)\(\left( {d{m^3}} \right)\)
soanvan.me
