Bài 5 trang 158 Vở bài tập toán 9 tập 2

Đề bài

Cho hai đường tròn \((O; R)\) và \((O’; r)\) tiếp xúc ngoài \((R>r)\). Hai tiếp tuyến chung \(AB\) và \(A’B’\) của hai đường tròn \((O), (O’)\) cắt nhau tại \(P\) (\(A\) và \(A’\) thuộc đường tròn \((O’)\), \(B\) và \(B’\) thuộc đường tròn \((O)\)). Biết \(PA=AB=4cm\). Tính diện tích hình tròn \((O’)\).

Lời giải chi tiết

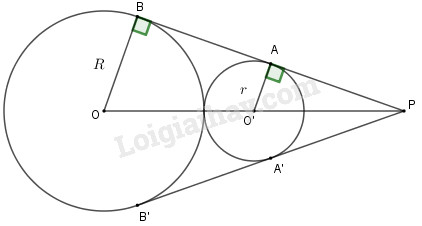
Vì \(AB\) là tiếp tuyến chung của hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) nên \(O'A //OB\) (cùng vuông góc với AP)

Gọi \(P\) là giao điểm của hai tiếp tuyến chung thì \(P\) thuộc đường nối tâm \(OO'.\)

Vì \(PA = AB \Rightarrow A\) là trung điểm của \(PB \Rightarrow PA = AB = \dfrac{{PB}}{2}\)

Xét tam giác \(POB\) có \(OB//O'A\) nên theo hệ quả định lý Ta-lét ta có

\(\dfrac{{O'A}}{{OB}} = \dfrac{{PO'}}{{PO}} = \dfrac{{PA}}{{PB}} = \dfrac{1}{2}\) 

Suy ra \(OB = 2O'A \) hay \(R = 2r\) 

Ta có \(PO' = OO' = R + r = 2r + r = 3r\)

Xét tam giác vuông \(PO'A\), theo định lý Pytago ta có \(P{O'^2} = O'{A^2} + P{A^2}\) hay \((3r)^2 = r^2 + {4^2} \Leftrightarrow 8{r^2} = 16\)\( \Leftrightarrow {r^2} = 2\)

Diện tích hình tròn \(\left( {O'} \right)\) là \(S = \pi {r^2} = 2\pi \) \(\left( {c{m^2}} \right)\) 

soanvan.me