Đề bài
Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang \(ABCD\) \(\left( {AB//C{\rm{D}}} \right)\) có \(AC = BD.\)
Qua \(B\) kẻ đường thẳng song song với \(AC\), cắt đường thẳng \(DC\) tại \(E.\) Chứng mình rằng:
a) \(∆BDE\) là tam giác cân.
b) \(∆ACD = ∆BDC.\)
c) Hình thang \(ABCD\) là hình thang cân.
Phương pháp giải - Xem chi tiết
Áp dụng:
- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.
- Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
- Nhận xét: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
Lời giải chi tiết
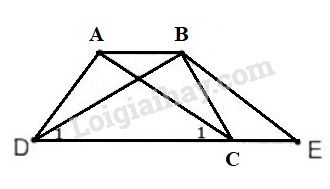

a) Hình thang \(ABEC\; (AB // CE)\) có hai cạnh bên \(AC, BE\) song song nên \( AC = BE\) (1)
Theo giả thiết \(AC = BD\) (2)
Từ (1) và (2) suy ra \(BE = BD\) nên \(\Delta BDE\) là tam giác cân.
b)
\(∆BDE\) cân (câu a) nên \( \widehat {{D_1}} = \widehat E\) (3)
\(AC//BE \) nên \( \widehat {{C_1}} = \widehat E\) (2 góc đồng vị) (4)
Từ (3) và (4) suy ra \( \widehat {{D_1}} = \widehat {{C_1}}\)
\(∆ACD\) và \( ∆BDC\) có:
+) \(AC = BD\) (giả thiết)
+) \(\widehat {{C_1}} = \widehat {{D_1}}\) (chứng minh trên)
+) \(CD\) cạnh chung
Do đó \(∆ACD = ∆BDC\) (c.g.c)
c) \(∆ACD = ∆BDC\) (câu b) suy ra \( \widehat {A{\rm{D}}C} = \widehat {BCD}\) (\(2\) góc tương ứng)
Hình thang \(ABCD\) có \( \widehat {A{\rm{D}}C} = \widehat {BCD}\) nên là hình thang cân.
soanvan.me
