Câu 7.
Khoanh tròn vào chữ cái trước câu trả lời đúng. Một hình thang cân có hiệu của hai góc bằng \(40^o\). Hai góc đó bằng
\(\eqalign{
& (A)\,\,{120^o}\,\,\text{và}\,\,{80^o} \cr
& (B)\,\,{100^o}\,\,\text{và}\,\,{60^o} \cr
& (C)\,\,{110^o}\,\,\text{và}\,\,{70^o} \cr
& (D)\,\,{105^o}\,\,\text{và}\,\,{65^o} \cr} \)
Hãy chọn câu trả lời đúng.
Phương pháp giải:
- Hình thang là tứ giác có hai cạnh đối song song
- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.
Lời giải chi tiết:
Giả sử có hình thang cân \(ABCD\) thỏa mãn bài toán như hình vẽ. Ta có:
\(\widehat A - \widehat D = {40^o}\Rightarrow \widehat A = \widehat D + {40^o}\)
Vì \(AB//CD\) nên \(\widehat A + \widehat D = {180^o}\)
\(\eqalign{
& \Rightarrow \widehat D + {40^o} + \widehat D = {180^o} \cr
& \Rightarrow 2\widehat D = {180^o} - {40^o} \cr
& \Rightarrow \widehat D = {140^o}:2 \cr
& \Rightarrow \widehat D = {70^o}\cr&\Rightarrow \widehat A = {70^o} + {40^o} = {110^o} \cr} \)
Chọn C.
Câu 8.
Điền các từ thích hợp (bằng nhau, bù nhau, không bằng nhau) vào chố trống (...)
a) Trong một hình thang cân, hai góc kề một đáy ...
b) Trong một hình thang cân, hai góc đối ...
c) Trong một hình thang cân, hai cạnh bên ... , hai đường chéo ...
d) Trong một hình thang cân có hai cạnh bên không song song, hai đáy ...
Phương pháp giải:
- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.
- Trong một hình thang cân, hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
- Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
Lời giải chi tiết:
Điền các từ thích hợp (bằng nhau, bù nhau, không bằng nhau) vào chố trống (...)
a) Trong một hình thang cân, hai góc kề một đáy bằng nhau.
b) Trong một hình thang cân, hai góc đối bù nhau.
c) Trong một hình thang cân, hai cạnh bên bằng nhau , hai đường chéo bằng nhau.
d) Trong một hình thang cân có hai cạnh bên không song song, hai đáy không bằng nhau.
Giải thích:
a) Theo định nghĩa hình thang cân.
b)
Hình thang cân \(ABCD\;(AB//CD)\)
\(\widehat A = \widehat B;\,\,\widehat C = \widehat D\) (theo định nghĩa)
Vì \(AB//CD\) nên \(\widehat A + \widehat D = {180^o}\) (hai góc trong cùng phía)
Mà \(\widehat A = \widehat B\) nên \(\widehat B + \widehat D = {180^o}\).
c) Tính chất hình thang cân.
d) Nhận xét hình thang: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
Câu 9.
Cho hình thang cân \(ABCD\;(AB//CD)\). Khoanh tròn vào chữ cái trước khẳng định không đúng.
\(\eqalign{
& (A)\,\widehat {ACD} = \widehat {BDC} \cr
& (B)\,\,\widehat {ABD} = \widehat {BDC} \cr
& (C)\,\,\widehat {ADB} = \widehat {ACB} \cr
& (D)\,\,\widehat {ABD} = \widehat {CBD} \cr} \)
Phương pháp giải:
- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc so le trong bằng nhau.
- Trong một hình thang cân, hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
Lời giải chi tiết:
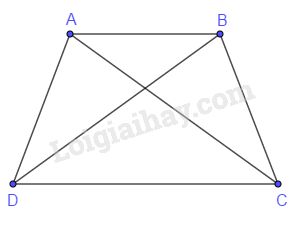
Xét \(\Delta ADC\) và \(\Delta BCD\) có:
+) \(AD=BC\) (vì \(ABCD\) là hình thang cân)
+) \(DC\) chung
+) \(\widehat D = \widehat C\) (vì \(ABCD\) là hình thang cân)
\(\Rightarrow \Delta ADC = \Delta BCD\,\,(c.g.c)\)
\( \Rightarrow \widehat {ACD} = \widehat {BDC}\)
\(AB//CD\) nên \(\widehat {ABD} = \widehat {BDC}\) (hai góc so le trong)
\( \widehat C = \widehat D \Rightarrow \widehat {ACD} + \widehat {ACB} \)\(= \widehat {BDC} + \widehat {ADB} \)
\( \text{ Mà }\widehat {ACD} = \widehat {BDC} \)
\( \Rightarrow \widehat {ADB} = \widehat {ACB} \)
Chọn D.
soanvan.me
