Đề bài
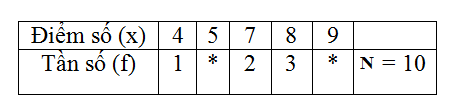
Điểm kiểm tra Toán của một tổ học tập được cho trong bảng sau:
Biết điểm trung bình của cả tổ là \(6,6\). Hãy điền các giá trị thích hợp vào hai ô còn trống (được đánh dấu *).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
B1: Đặt số học sinh được điểm \(5\) là \(x\), tìm điều kiện của \(x\)
B2: Biểu diễn các đại lượng còn lại theo \(x\).
B3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng theo \(x\) và giải phương trình đó.
B4: Kết luận.
Lời giải chi tiết
Gọi \(x\) là số học sinh (tần số) được điểm \(5\) (\(0 < x < 10\); \(x\) nguyên)
Tần số của điểm \(9\) là: \(10 - (1 + 2 + 3 + x) = 4 - x\)
Điểm trung bình của cả tổ bằng \(6,6\) nên ta có phương trình:
\(\dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}} \)\(\,= 6,6\)
\( \Leftrightarrow \dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}}\)\(\, = \dfrac{{10.6,6}}{{10}}\)
\(⇔ 4 + 5x + 14 + 24 + 36 - 9x = 66\)
\(⇔ -4x + 78 = 66\)
\( \Leftrightarrow - 4x = 66 - 78\)
\(⇔ -4x = -12\)
\( \Leftrightarrow x = \left( { - 12} \right):\left( { - 4} \right)\)
\(⇔ x = 3\) (thỏa mãn điều kiện)
Tần số của 9 là: \(4-x=4-3=1\)
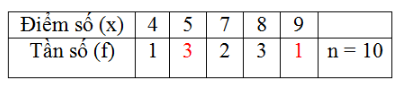
Vậy tần số của điểm \(5\) là \(3\) và tần số của điểm \(9\) là \(1\).
Ta điền như sau:
soanvan.me