Đề bài
Tam giác \(ABC\) có hai trung tuyến \(AM\) và \(BN\) vuông góc với nhau. Hãy tính diện tích tam giác đó theo \(AM\) và \(BN\)
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích tam giác bằng nửa tích một cạnh và chiều cao tương ứng: \(S=\dfrac{1}{2}ah\)
Lời giải chi tiết
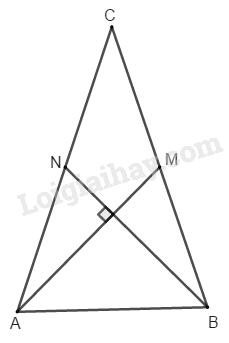
Tứ giác \(ABMN\) có hai đường chéo vuông góc.
\({S_{ABMN}} = \eqalign{1 \over 2}AM.BN\)
\(∆ ABM\) và \(∆ AMC\) có chung chiều cao kẻ từ \(A,\) cạnh đáy \(BM = MC\)
\( \Rightarrow {S_{ABM}} = {S_{AMC}} = \eqalign{1 \over 2}{S_{ABC}}\)
\(∆ MAN\) và \(∆ MNC\) có chung chiều cao kẻ từ \(M,\) cạnh đáy \(AN = NC\)
\(\eqalign{ & \Rightarrow {S_{MAN}} = {S_{MNC}} = {1 \over 2}{S_{AMC}} } \) \(\eqalign{ = {1 \over 4} {S_{ABC}}} \)
\(\eqalign{{S_{ABMN}} = {S_{ABM}} + {S_{MNA}}} \)
\(= \eqalign{{1 \over 2}{S_{ABC}} + {1 \over 4}{S_{ABC}} }\)
\(= \eqalign{{3 \over 4}{S_{ABC}} }\)
\(\Rightarrow \eqalign{{S_{ABC}} = \eqalign{4 \over 3}{S_{ABMN}} }\) \(= \eqalign{{4 \over 3}.\eqalign{1 \over 2}.AM.BN =\eqalign {2 \over 3}AM.BN }\)
soanvan.me
