Đề bài
Cho lục giác \(ABCDEF,\) có \(AB = BC\) \(= 3\, cm\) và\( ED = 4 \,cm.\) Biết rằng \(ED\) song song với \(AB,\, AB\) vuông góc với \(BC, \,FE\) vuông góc với \(FA\) và \(FE = FA.\) Qua điểm \(A\) kẻ đường thẳng \(d\) song song với \(BC.\) Gọi \(K\) là giao điểm của \(d\) và \(ED,\) biết \(AK = 4\,cm,\, KD = 1\,cm.\) Tính diện tích của lục giác đó.
Phương pháp giải - Xem chi tiết
Chia lục giác đã cho thành các hình thang, hình tam giác. Sau đó lần lượt tính diện tich hình thang và hình tam giác đã chia rồi tính diện tích hình lục giác đã cho của bài toán.
Lời giải chi tiết
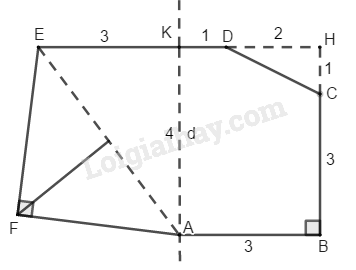
Gọi \(H\) là giao điểm của hai đường thẳng \(ED\) và \(BC.\) Khi đó, \(ABHE\) là hình thang và diện tích hình thang \(ABHE\) là: \(S_1=\dfrac{1}{2}(AB+EH).BH\) \(= \dfrac{1}{2} (3+6).4=18\ (cm^2)\)
Diện tích tam giác vuông \(DHC\) là: \(S_2=\dfrac{1}{2} DH.HC\) \(=\dfrac{1}{2}.2.1=1\,(cm^2)\)
Trong tam giác vuông \(AKE\), theo định lý Pytago ta có:
\(A{E^2} = K{E^2} + K{A^2} \)\(= {3^2} + {4^2} = 25\)
Suy ra \(EA=5\,(cm)\)
Trong tam giác vuông \(FEA\) có \(FE=FA\) nên theo định lý Pytago ta có:
\(F{E^2} + F{A^2} = E{A^2} \Leftrightarrow 2F{E^2} = 25\)
\(\Leftrightarrow FE^2=\dfrac{25}{2}\)
Từ đó diện tích của tam giác \(FEA\) là: \(S_3= \dfrac{1}{2}.FA.FE = \dfrac{1}{2}F{E^2} \)\(= \dfrac{1}{2}.\dfrac{{25}}{2}=\dfrac{25}{4}\,(cm^2)\)
Vậy diện tích của lục giác đã cho là: \(S=S_1+S_3-S_2\) \(= 18+\dfrac{25}{4}-1=\dfrac{93}{4}\) \((cm^2)\)
soanvan.me
