Đề bài
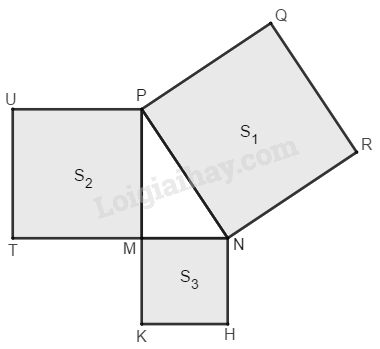
Cho hình bs.32 (tam giác \(MNP\) vuông tại đỉnh \(M\) và \(NRQP,\, PUTM,\, MKHN\) đều là hình vuông, còn \(S_1,\, S_2,\,S_3\) tương ứng là diện tích của mỗi hình. Quan hệ nào sau đây là đúng?
(A) \(S_3+S_2=S_1\)
(B) \({S_3}^2+{S_2}^2={S_1}^2\)
(C) \(S_3+S_2>S_1\)
(D) \({S_3}^2+{S_2}^2<{S_1}^2\)
Phương pháp giải - Xem chi tiết
Áp dụng định lý Pi - ta - go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Diện tích hình vuông cạnh \(a\) bằng \(a^2\)
Lời giải chi tiết
Gọi độ dài của \(PM ,\,MN, \,PN\) lần lượt là \(a,\, b,\, c.\)
Tam giác \(PMN\) vuông tại \(M,\) theo định lý Pi – ta - go ta có: \({a^2} + {b^2} = {c^2}\)
Do các tứ giác \( PUTM,\ NRQP,\, MKHN\) đều là hình vuông và có độ dài các cạnh lần lượt là \(a, \,b,\,c\) nên diện tích của chúng tương ứng là: \({a^2},{b^2},{c^2}\)
Như vậy: \({S_1} = {c^2},{S_2} = {a^2},{S_3} = {b^2}\) mà \({a^2} + {b^2} = {c^2}\)
Nên ta có hệ thức: \({S_2} + {S_3} = {S_1}\)
Chọn (A)
soanvan.me
