Đề bài
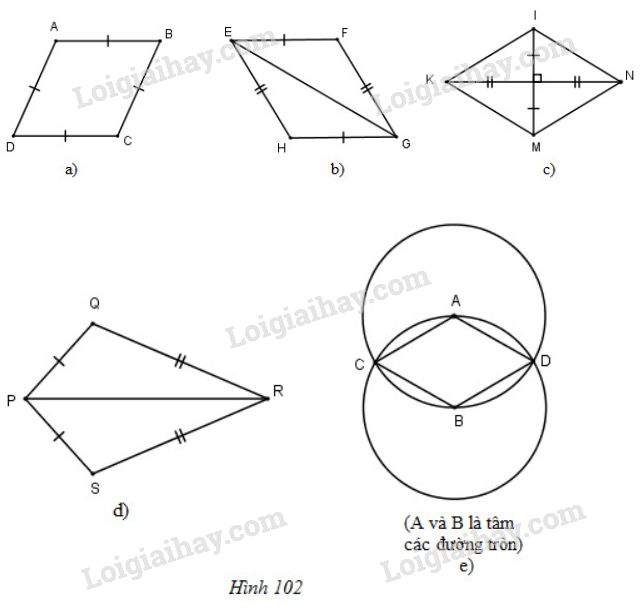
Tìm các hình thoi trên hình \(102.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng: Dấu hiệu nhận biết hình thoi:
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
+) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
+) Tứ giác có bốn cạnh bằng nhau là hình thoi.
Lời giải chi tiết
Các tứ giác ở hình \(102\;\; a, b, c, e\) là hình thoi.
- Ở hình \(102a\), tứ giác \(ABCD\) có bốn cạnh bằng nhau nên là hình thoi (theo định nghĩa)
- Ở hình \(102b\),
Tứ giác \(EFGH\) có \(EF=HG\), \(EH=FG\) nên tứ giác \(EFGH\) là hình bình hành.
Hơn nữa ta lại có \(EG\) là phân giác của góc \(FEH\) (giả thiết)
Do đó \(EFGH\) là hình thoi (theo dấu hiệu nhận biết hình thoi)
- Ở hình 102c, \(KINM\) có hai đường chéo \( IM\) và \(KN\) cắt nhau tại trung điểm của mỗi đường
\(\Rightarrow\) tứ giác \(KINM\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Mà \(IM \bot KN\left( {gt} \right) \Rightarrow \) hình bình hành \(KINM\) là hình thoi (dấu hiệu nhận biết hình thoi)
-Ở hình 102e, \(ADBC\) là hình thoi (theo định nghĩa), vì:
\(AC = AD = AB \,(C, B, D\) cùng thuộc đường tròn tâm \(A).\)
\(BC = BA = BD\, (A, C, D\) cùng thuộc đường tròn tâm \(B)\)
\(⇒ AC = CB = BD = DA\)
\(⇒ ACBD\) là hình thoi.
Tứ giác trên hình 102d không là hình thoi (vì có 4 cạnh không bằng nhau).
soanvan.me
