Đề bài
Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có một góc vuông là hình chữ nhật.
Lời giải chi tiết
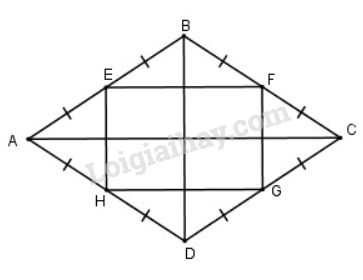
Xét hình thoi \(ABCD\), gọi \( E, F, G, H\) lần lượt là trung điểm của \( AB, BC, CD, AD\).
Ta có: \(EB = EA, FB = FC\) (giả thiết )
nên \(EF\) là đường trung bình của \(∆ABC\) (dấu hiệu nhận biết đường trung bình của tam giác )
\( \Rightarrow \) \(EF // AC,EF=\dfrac{AC}2\) (tính chất đường trung bình của tam giác)
Do \(HD = HA, GD = GC\) (giả thiết )
\( \Rightarrow \) \(HG\) là đường trung bình của \(∆ADC\) (dấu hiệu nhận biết đường trung bình của tam giác )
\( \Rightarrow \) \(HG // AC,HG=\dfrac{AC}2\) (tính chất đường trung bình của tam giác)
\( \Rightarrow \) \(EF // HG\) (cùng // \(AC\)) và \( EF=HG\,(=\dfrac{AC}2)\)
Suy ra \(EFGH\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Ta có: \(EB = EA, AH = HD\) (giả thiết )
nên \(EH\) là đường trung bình của \(∆ABD\) (dấu hiệu nhận biết đường trung bình của tam giác )
\( \Rightarrow \) \(EH // BD\) (tính chất đường trung bình của tam giác)
Ta có \(EF // AC\) (chứng minh trên) và \(BD ⊥ AC\) (tính chất hình thoi \(ABCD\))
\( \Rightarrow \) \(BD ⊥ EF\)
Mà \(EH // BD\) (chứng minh trên)
\( \Rightarrow \) \(EF ⊥ EH\)
\( \Rightarrow \) \(\widehat{FEH} = 90^0\)
Hình bình hành \(EFGH\) có \(\widehat{E} = 90^0\) nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
soanvan.me
