Đề bài
Chứng minh rằng:
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
+) Hai điểm \(A\) và \(A'\) gọi là đối xứng nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của \(AA'\).
Lời giải chi tiết
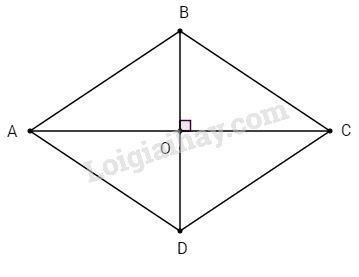
a) Hình bình hành nhận giao điểm hai đường chéo là tâm đối xứng. Hình thoi cũng là một hình bình hành nên giao điểm hai đường chéo hình thoi là tâm đối xứng của hình thoi.
b) Vì \(ABCD\) là hình thoi nên \(BD\bot AC\) tại \(O\) và \(O\) là trung điểm của \(BD\) và \(AC\)
Suy ra \(BD\) là đường trung trực của \(AC\) và \(AC\) là đường trung trực của \(BD\)
Do đó \(A\) đối xứng với \(C\) qua \(BD.\)
\(B\) và \(D\) cũng đối xứng với chính nó qua \(BD.\)
Nên \(BD\) là trục đối xứng của hình thoi.
Vì \(AC\) là đường trung trực của \(BD\) nên \(B\) đối xứng với \(D\) qua \(AC.\)
\(A\) và \(C\) cũng đối xứng với chính nó qua \(AC.\)
Nên \(AC\) là trục đối xứng của hình thoi.
soanvan.me
