Đề bài
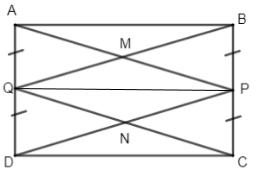
Cho hình chữ nhật ABCD; P, Q lần lượt là trung điểm của BC và AD. Gọi M là giao điểm của AP và BQ, N là giao điểm của CQ và DP. Chứng minh: Tứ giác MPNQ là hình thoi.
Phương pháp giải - Xem chi tiết
Sử dụng:
Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành
Hình bình hành có một góc vuông là hình chữ nhật
Hình bình hành có hai cạnh kề bằng nhau là hình thoi
Lời giải chi tiết
Vì ABCD là hình chữ nhật nên \(AD=BC,AB=CD\) và \(AD//BC,AB//CD\)
Ta có Q, P lần lượt là trung điểm của AD và BC nên AQ = QD = BP = PC và \(AQ// CP,\;DQ//BP.\)
Do đó tứ giác sau là các hình bình hành APCQ, BPDQ \(\Rightarrow AP// CQ\) và \(BQ//DP\)
\( \Rightarrow MNPQ\) là hình bình hành
Mặt khác tứ giác ABPQ có AQ//BP, AQ=BP nên ABPQ là hình bình hành. Lại có góc A bằng \(90^0\) (do ABCD là hình chữ nhật) nên ABPQ là hình chữ nhật.
\( \Rightarrow MQ = MP\) (tính chất hai đường chéo hình chữ nhật)
Vậy MPNQ là hình thoi (hình bình hành có hai cạnh kề bằng nhau).
soanvan.me