Đề bài
Cho hình bình hành ABCD có diện tích 120 m2. Gọi M và N lần lượt lã trung điểm của BC và CD. BN cắt DM tại P. Tính diện tích tứ giác ABPD.
Lời giải chi tiết
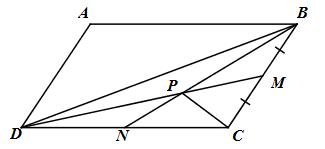
\({S_{BCN}} = {1 \over 2}{S_{BCD}}\) (do \(CN = {1 \over 2}CD\)) và \({S_{BCD}} = {1 \over 2}{S_{ABCD}}\) (tứ giác ABCD là hình bình hành)
Do đó \({S_{BCN}} = {1 \over 4}{S_{ABCD}} = {1 \over 4}.120 = 30\,\,\left( {{m^2}} \right)\)
Tương tự: \({S_{DCM}} = 30\,\,\left( {{m^2}} \right)\)
\({S_{BCN}} = S{ _{DCM}} \Rightarrow {S_{DNP}} + {S_{CMPN}} \)\(\;= {S_{BMP}} + {S_{CMPN}}\)
\( \Rightarrow {S_{DNP}} = {S_{BMP}}\)
Mặt khác \({S_{BMP}} = {S_{CMP}}\,\,\left( {BM = CM} \right),\)
\({S_{DNP}} = {S_{CPN}}\,\,\left( {DN = CN} \right)\)
Do đso \({S_{BMP}} = {S_{CMP}} = {S_{CPN}} = 30:3 = 10\,\,\left( {{m^2}} \right)\)
Do vậy \({S_{ABPD}} = {S_{ABCD}} - {S_{DCM}} - {S_{BMP}} \)\(\,= 120 - 30 - 10 = 80\,\,\left( {{m^2}} \right)\)
soanvan.me
