Đề bài
Cho hình chữ nhật ABCD có trung điểm các cạnh lần lượt là M, N, P, Q.
a) Chứng minh rằng MNPQ là một hình thoi.
b) Cho biết diện tích hình chữ nhật ABCD lả 20cm2. Tính diện tích hình thoi MNPQ.
Lời giải chi tiết
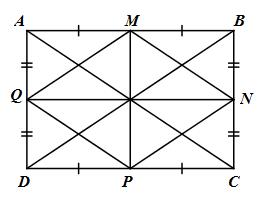
a) M, N lần lượt là trung điểm của AB và BC (gt)
\( \Rightarrow MN\) là đường trung bình của tam giác ABC
\( \Rightarrow MN//AC\) và \(MN = {{AC} \over 2}\,\,\,\,\left( 1 \right)\)
Q, P lần lượt là trung điểm của AD và CD (gt)
\( \Rightarrow QP\) là đường trung bình của tam giác ACD
\( \Rightarrow QP//AC\) và \(QP = {{AC} \over 2}\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow MN//QP\) và \(MN = QP\).
Do đó tứ giác MNPQ là hình bình hành.
Q, M lần lượt là trung điểm của AB và AB (gt)
\( \Rightarrow QM\) là đường trung bình của tam giác ABD
\( \Rightarrow QM = {{BD} \over 2}\)
Mà \(MN = {{AC} \over 2}\) và \(BD = AC\) (ABCD là hình chữ nhật) nên \(QM = MN\)
Hình bình hành MNPQ có \(QM = MN\) nên là hình thoi.
b) Tứ giác AMPD có AM // DP và \(AM = PD\,\,\left( { = {{AB} \over 2}} \right) \Rightarrow \) Tứ giác AMPD là hình bình hành \( \Rightarrow MP = AD\).
Tứ giác ABNQ có AQ // BN và \(AQ = BN\,\,\left( { = {{AD} \over 2}} \right) \Rightarrow \) Tứ giác ABNQ là hình bình hành \( \Rightarrow AB = QN\)
Tứ giác MNPQ là hình thoi.
Do đó \({S_{MNPQ}} = {1 \over 2}MP.QN = {1 \over 2}AD.AB\)\(\, = {1 \over 2}{S_{ABCD}} = 10\,\,\left( {c{m^2}} \right)\)
soanvan.me
